Phương pháp khai thác theo chiều ngang để trích xuất các tập phổ biến

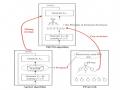
Qui trình thực hiên gồm 4 bước:

(0) Thiết lập cây FP-Tree

(1) Thiết lập cơ sở mẫu điều kiện cho mỗi hạng mục phổ biến (mỗi nút trên cây FP-Tree):

Bắt đầu từ mẫu phổ biến cuối bảng của cây FP-Tree

Duyệt cây FP-Tree theo kết nối của mỗi hạng mục phổ biến

Gom tất cả đường dẫn tiền tố biến đổi của hạng mục để tạo cơ sở mẫu điều kiện.

Ví dụ 2.11:

Xây dựng cơ sở mẫu điều kiện:

Bắt đầu từ mẫu phổ biến cuối bảng của cây FP-Tree: hạng mục p.

Duyệt cây FP-Tree theo kết nối của mỗi hạng mục phổ biến p.

Gom tất cả đường dẫn tiền tố biến đổi của hạng mục p để tạo cơ sở mẫu điều kiện cho p.

hạng

Độ phổ biến

mục

f:4

c:3

b:1

a:3

m:2

b:1

p:2

m:1

{}

c:1

b:1

p:1

hạng mục	Cơ sở mẫu điều kiện
p	fcam:2, cb:1

Có thể bạn quan tâm!

Xem toàn bộ 84 trang tài liệu này.

Ghi chú: Tần xuất xuất hiện của fcam = tần xuất xuất hiện của p của nhánh

Hình 2.6 Cơ sở mẫu điều kiện cho nút p Tiếp tục với mẫu phổ biến của cây FP-Tree: hạng mục m.

Duyệt cây FP-Tree theo kết nối của mỗi hạng mục phổ biến m.

Gom tất cả đường dẫn tiền tố biến đổi của hạng mục m để tạo cơ sở mẫu điều kiện cho m.

c:3

a:3

hạng mục	Cơ sở mẫu điều kiện
m	fca:2, fcab:1

hạng

Độ phổ biến

mục

b:1

m:2 b:1

p:2

{}

f:4

m:1

c:1

b:1

p:1

Hình 2.7 Cơ sở mẫu điều kiện kiện cho nút m Tiếp tục với các mẫu phổ biến còn lại của cây FP-Tree:

hạng Độ phổ biến

mục

f:4

c:3

b:1

a:3

b 3

m:2

b:1

p:2

m:1

{}

c:1

b:1

p:1

hạng mục	Cơ sở mẫu điều kiện
c	f:3
a	fc:3
b	fca:1, f:1, c:1
m	fca:2, fcab:1
p	fcam:2, cb:1

Hình 2.8 Cơ sở mẫu điều kiện cho các nút của cây FP-Tree

(2) Thiết lập cây FP-Tree điều kiện từ mỗi cơ sở mẫu điều kiện. Với mỗi cơ sở mẫu:

Đếm số lượng mỗi mẫu trong cơ sở mẫu. Xác định tập phổ biến của mẫu cơ sở

Xây dựng cây FP-Tree điều kiện cho tập phổ biến của mẫu cơ sở (thực hiện tương tự như bước (0)).

Ví dụ 2.12: Xây dựng cây FP-Tree điều kiện

Với cơ sở mẫu điều kiện cho p là: {fcam:2, cb:1}

Đếm số lượng mỗi mẫu trong cơ sở mẫu ta có: f:2, c:3, a:2, m:2, b:1 và với minsup = 60% cho nên chỉ còn c:3 là mẫu phổ biến trên cơ sở mẫu điều kiện của p.

{}

c:3

Xây dựng cây FP-Tree cho tập phổ biến của cơ sở mẫu điều kiện cho p:

hạng mục

Độ phổ biến
c	3

Hình 2.9 Cây FP-Tree cho tập phổ biến của cơ sở mẫu điều kiện cho p Với cơ sở mẫu điều kiện cho m là: {fca:2, fcab:1}

Đếm số lượng mỗi mẫu trong cơ sở mẫu ta có: f:3, c:3, a:3, b:1 và với minsup

= 60% cho nên chỉ còn f:3, c:3, a:3 là các mẫu phổ biến trên cơ sở mẫu điều kiện của m.

hạng Độ phổ biến

Xây dựng cây FP-Tree cho tập phổ biến của mẫu cơ sở điều kiện cho m:

mục
f	3
c	3
a	3

{}

f:3

c:3

a:3

Hình 2.10 Cây FP-Tree cho tập phổ biến của mẫu cơ sở điều kiện cho m Tương tự cho các cơ sở mẫu điều kiện còn lại, chúng ta thu được:

mục

Cơ sở mẫu điều kiện	Cây điều kiện FP tree
p	{(fcam:2), (cb:1)}	{(c:3)}\|p
m	{(fca:2), (fcab:1)}	{(f:3, c:3, a:3}\|m
b	{(fca:1), (f:1), (c,1)}	{}
a	{(fc:3)}	{(f:3, c:3}\|a
c	{(f:3)}	{(f:3)}\|c
f	{}	{}

Hạng

Bảng 2.11 Bảng kết quả cây FP-Tree điều kiện từ mỗi cơ sở mẫu điều kiện

(3) Khai thác đệ qui cây FP-Tree điều kiện phát triển mẫu phổ biến cho đến khi cây FP-Tree điều kiện chỉ chứa 1 đường dẫn duy nhất tạo ra tất cả các tổ hợp của mẫu phổ biến:

Xây dựng tập phổ biến dựa trên nguyên lý mở rộng mẫu phổ biến và tính chất mở rộng mẫu:

Giả sử  là tập phổ biến trong CSDL, B là cơ sở mẫu điều kiện của ;  là một hạng mụcset trong B. Khi đó  là tập phổ biến trong CSDL khi và chỉ khi  là phổ biến trong B.

Ví dụ 2.13:

“abcdef” là mẫu phổ biến khi và chỉ khi “abcde” là mẫu phổ biến và “f” là phổ biến trong tập các giao dịch chứa “abcde”

Trường hợp cây chỉ có đường dẫn đơn (Đường dẫn đơn là đường dẫn chỉ có 01 đường đi duy nhất từ nút gốc đến nút lá)

Giả sử cây FP-Tree là cây T có một đường dẫn đơn P; tập phổ biến cuối cùng của T sinh ra bằng cách liệt kê tất cả các tổ hợp của đường dẫn con thuộc P.

Ví dụ 2.14:

{}

Cây FP-Tree điều kiện cho p là cây có đường dẫn đơn

Hạng mục

Độ phổ biến

c:3

Hình 2.11 Tất cả mẫu phổ biến liên quan đến p là: p:3 và cp:3

Hạng Độ phổ biến

mục

Cây FP-Tree điều kiện cho m là cây có đường dẫn đơn:

{}


f:3

c:3

a:3

Hình 2.12 Tất cả mẫu phổ biến liên quan đến m là: m:3, fm:3, cm:3, am:3, fcm3:, fam:3, cam:3, fcam:3

Trường hợp cây không chỉ có đường dẫn đơn: Xem xét các cây FP-Tree chỉ có 01 đường dẫn đơn và các cây FP-Tree gồm nhiều nhánh một cách riêng biệt.

Việc phân chia cây nhiều nhánh thành cây có một đường dẫn đơn thực hiện đệ quy gọi FP_Growth(FP-Tree, Null).

Nhận xét thuật toán FP-Growth:

Ưu điểm:

Hiệu quả hơn so với Apriori.

Phân chia và kiểm soát quá trình xử lý.

Sử dụng cây FP-Tree để biểu diễn các mẫu phổ biến thì dữ liệu giảm rất đáng kể so với cách biểu diễn trong CSDL.

Nhược điểm:

Không thể xây dựng cây FP-Tree trong bộ nhớ chính khi CSDL là lớn.

Mất nhiều thời gian và gặp trở ngại khi cập nhật lại cây khi cây tăng trưởng về mặt kích thước.

Đánh giá:

Điểm nổi bật của thuật toán này là chỉ quét cơ sở dữ liệu hai lần, và không cần phát sinh tập ứng viên. Chính điều này làm cho FP-Growth nhanh hơn Apriori. Trong nghiên cứu của mình, Han đã chứng minh rằng phương pháp của ông nhanh hơn so với các phương pháp tuần tự khác trong việc khai thác tập phổ biến như các thuật toán Apriori,…

2.3.3. Thuật toán CLOSET

Thuật toán CLOSET [6] là mở rộng của thuật toán FP-growth [4], trong đó xây dựng một cây FP-Tree và đệ quy có điều kiện cây FP-Tree từ dưới lên để khai thác tập đóng:

1. Cho Y là tập các mục trong f_list sao cho chúng xuất hiện trong mọi giao tác của DB, thêm XY vào FCI nếu nó không phải là một tập con của FCI với cùng độ phổ biến;

2. Xây dựng FP-Tree cho DB, các mục đã được trích xuất nên được loại trừ

3. Trích xuất các tập đóng phổ biến nếu có thể

4. Xây dựng cơ sở dữ liệu có điều kiện cho tất cả các hạng mục còn lại trong f_list, đồng thời tính toán độ phổ biến cho mục cục bộ của các cơ sở dữ liệu có điều kiện này.

5. Đối với mỗi mục còn lại trong f_list, bắt đầu từ mục cuối cùng, gọi đệ quy CLOSET (iX; DB|i; f_listi; FCI) nếu iX không phải là một tập con của bất kỳ tập phổ biến đóng với cùng độ phổ biến, khi đó DB|i ký hiệu i-cond DB và f_listi là mục phổ biến tương ứng.

Thuật toán CLOSET

Input: CSDL giao tác TDB và minsup; Output: FCI;

Method:

1. Khởi tạo: FCI 

2. Tính độ phổ biến: Duyệt CSDL giao tác gán vào f list;

3. CLOSET(; TDB; f_list; FCI). Subroutine CLOSET(X; DB; f_list; FCI) Tham số:

X: các tập phổ biến nếu DB là X-cond DB

 nếu DB là TDB;

DB: transaction database of conditional database;//cơ sở dữ liệu có điều kiện f_list: danh sách các hạng mục phổ biến của DB;

FCI: Tập phổ biến.

Hình 2.13 Thuật toán CLOSET

Ví dụ 2.15: Cho một CSDL giao tác như sau:

Mã giao tác

Nội dung giao tác
1	a, c, d, e, f
2	a, b, e
3	c, e, f
4	a, c, d, f
5	c, e, f

Bảng 2.12 CSDL giao tác gồm 5 giao tác và 5 hạng mục

f_list:{c:4, e:4, f:4, a:3, d:2}

Output F.C.I: cfad:2

Output F.C.I: e:4

Output F.C.I: cf:4, cef:3

Output F.C.I: a:3

Minh họa thuật toán CLOSET

TDB

cefad

cef

cfad

cef

d-cond DB

(d:2)

cefa

cfa

a-cond DB

(a:3)

cef

f-cond DB

(f:4)

ce:3

e-cond DB

(e:4)

c:3

ea-cond DB (ea:2)

Output F.C.I: ae:2

Hình 2.14 Thuật toán CLOSET khai thác tập phổ biến đóng

Diễn giải thuật toán:

Trong CSDL bảng 2.12 với minsup = 2, sử dụng phương pháp chia để trị trong khai thác các tập phổ biến đóng như trong hình 2.14

1. Tìm hàng mục phổ biến: Duyệt CSDL để tìm tập hợp các hạng mục phổ biến và lập một danh sách hạng mục phổ biến, được gọi là f_list, f_list = {c: 4; e: 4; f: 4; a: 3; d: 2}, trong đó các mục được sắp xếp giảm dần theo độ phổ biến như trong Hình 2.14

2. Kỹ thuật chia để trị: Tất cả các tập đóng phổ biến có thể được chia thành 5 tập con không chồng lên nhau dựa trên f_list:

- Các tập con chứa mục d,

- Các tập con chứa mục a và không chứa mục d,

- Các tập con chứa mục f và không chứa mục a và d,

- Các tập con chứa mục e và không chứa mục f, a và d

- Các tập con chỉ chứa mục c

3. Quá trình tìm các tập con của các tập đóng phổ biến: Các tập con của các tập đóng phổ biến có thể được khai thác bằng cách xây dựng các cơ sở dữ liệu tương ứng và điều kiện đệ quy của chúng.

(a) Tìm các tập đóng phổ biến có chứa d. Chỉ giao tác có chứa d là cần thiết. Cơ sở dữ liệu có điều kiện, được ký hiệu là TDB|d, chứa tất cả các giao tác có d, đó là {cefa, cfa}. Chú ý hạng mục bị loại bỏ trong mỗi giao tác vì nó xuất hiện trong mọi giao tác của cơ sở dữ liệu có điều kiện.

Độ phổ biến của d là 2. Các mục c, f và a xuất hiện hai lần tương ứng trong TDB|d. Có nghĩa là mọi giao tác có chứa d cũng chứa c, f và a. Hơn nữa, e là không phổ biến vì nó chỉ xuất hiện một lần trong TDB|d. Do đó, cfad: 2 là tập phổ biến đóng. Quá trình khai thác của TDB|d kết thúc.

(b) Tìm các tập phổ biến đóng có chứa a không có d. Tương tự, cơ sở dữ liệu có điều kiện, TDB|a = {cef; e; cf}. Mục d trong các giao tác như vậy được bỏ qua, vì các tập phổ biến đóng có chứa d đã được tìm thấy trong TDB|d. Vì sup (a) = 3 và không có bất kỳ mục nào xuất hiện trong mọi giao tác của TDB|a, như vậy a: 3 là một mục đóng.