Kiểm Định Nhân Quả Dumitrescuhurlin Dữ Liệu Bảng

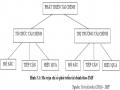
các nhu cầu khác nhau của TTKT ở các giai đoạn phát triển kinh tế khác nhau. Nhìn chung, sự phát triển của FS tối ưu phải phù hợp với lý thuyết lợi thế so sánh (Lin và cộng sự, 2013). Do vậy, đối với các ngành với rủi ro thấp và tỷ lệ thu hồi vốn đầu tư ổn định, các TGTC (ngân hàng) hoạt động hiệu quả hơn, nên mức độ phát triển nhanh hơn so với TTTC. Ngược lại, đối với các ngành công nghệ tiên phong với công nghệ cao hơn và rủi ro nhiều hơn, CTTC dựa trên ngân hàng thì thích hợp hơn và tăng trưởng nhanh hơn. Về cơ bản, chính sản lượng biên của các nguồn vốn tài chính khác nhau đóng vai trò là cầu nối liên kết CTTC và TTKT (Liu và Zhang, 2020). Do đó, CTTC tối ưu phải thay đổi và thay đổi ở các giai đoạn phát triển khác nhau của nền kinh tế. Hay nói cách khác, CTTC tối ưu không chỉ đơn giản là CTTC dựa trên ngân hàng hoặc dựa trên thị trường mà phụ thuộc vào hệ thống CTTC nào phù hợp hơn với mỗi một quốc gia ở một giai đoạn phát triển kinh tế cụ thể (Lin & Monga, 2010; Liu & Zhang, 2020). Và CTTC tối ưu phản ánh sự kết hợp của các lý thuyết cạnh tranh của CTTC (Song & Thakor, 2010; Kpodar & Singh, 2011).

Thứ hai, khi giảm bớt giả định về giới hạn khả năng lao động, mô hình tăng trưởng tân cổ điển mở rộng có thể được viết lại như sau:

(3.30)

Trong đó: L là số lượng lực lượng lao động

Với giả thiết hàm sản xuất là đồng nhất, phương trình (3.30) có thể được viết lại như sau:

(3.31)

Dựa trên Tiến bộ kỹ thuật trung tính Hicks, phương trình sai phân tương ứng: (3.32)

Trong đó: , , là đạo hàm riêng lần lượt của trên , FS, và

Có thể bạn quan tâm!

Xem toàn bộ 328 trang tài liệu này.

Lấy logarit hai vế:

(3.33)

Trong đó: C là hằng số biểu thị trình độ công nghệ.

Khi đó, theo mô hình tăng trưởng của Solow, hàm sản xuất có thể được giả định với để đáp ứng với hiệu suất không đổi theo quy mô với Tiến bộ kỹ thuật trung tính Hicks, phương trình (3.33) được viết lại theo sau:

(3.34)

Hàm sản suất đơn giản hóa:

(3.35)

Như vậy, phương trình (3.35) có thể được sử dụng để kiểm tra tác động của CTTC lên TTKT. Khi đó, để phân tích tác động của CTTC lên TTKT tại mẫu nghiên cứu của luận án với nhóm AE và DE, mô hình kinh tế lượng dữ liệu bảng dựa trên phương trình (3.35) với các biến kiểm soát được lựa chọn dựa trên nghiên cứu của

Arena (2008), DemirgüçKunt và cộng sự (2013), được biểu thị theo sau:

Liu và Zhang (2020), Chu (2020)

(3.36)

Trong đó: CONTROL là các biến kiểm soát lần lượt là:

TRADE Độ mở thương mại, được đưa vào mô hình để đánh giá tầm quan trọng của các yếu tố quốc tế trong tác động đến hoạt động kinh tế.

HC Chỉ số nguồn vốn con người đại diện cho nguồn nhân lực, thể tổng thể các tiềm năng lao động của một quốc gia.

hiện

GDPP0 (GDP bình quân đầu người ban đầu), giá trị GDPP năm 2004 được lựa chọn là GDPP ban đầu để kiểm soát hiệu ứng hội tụ vì các nền kinh tế kém phát triển hơn sẽ có xu hướng phát triển nhanh hơn các nền kinh tế giàu có hơn.

Nếu ước lượng hệ số dương và có ý nghĩa thống kê thì quan điểm CTTC

dựa trên thị trường được ủng hộ. Ngược lại, nếu hệ số âm thì quan điểm dựa trên ngân hàng được ủng hộ.

Để phân tích liệu rằng tác động của CTTC lên TTKT có bị ảnh hưởng bởi mức độ PTTC hay không, luận án đưa thêm biến tương tác giữa CTTC và PTTC dựa trên cách đo lường của Ergungor (2008) và Chu (2020) theo sau:

(3.37)

Trong đó: FDL là mức độ PTTC được tính toán dựa theo cách đo lường của Ergungor (2008) và Chu (2020), bằng tổng giá trị giao dịch TTCK trên GDP nhân với tín dụng tư nhân được cung cấp bởi gửi tiền ngân hàng và các TCTC khác trên GDP.

là hệ số tương tác giữa CTTC và mức độ PTTC. Nếu dương và có ý nghĩa thống kê cho thấy tầm quan trọng trong tác động đến TTKT của thị trường so với ngân hàng tăng lên cùng với mức độ PTTC và ngược lại.

Luận án sử

dụng GMM hệ

thống hai bước (Blundell & Bond, 1998;

Roodman, 2009) để kiểm định tác động của CTTC lên TTKT khi có ảnh hưởng của

mức độ PTTC. Phương pháp này cho phép tương quan bậc một với sai số, giải

quyết được các vấn đề phương sai thay đổi và tự tương quan của thành phần sai số

nhiễu (Roodman, 2009). Theo Hwang và Sun (2018), từ

khi GMM được sử

dụng

rộng rãi, thì GMM hai bước cũng được sử dụng để cải thiện tính hiệu quả của ước tính GMM và tính vững của các kiểm định liên quan. Các kết quả kiểm định thống kê dựa trên ước lượng GMM hai bước cũng có kết quả vững hơn so với các ước

tính dựa trên ước lượng GMM một bước. Một số kiểm định hậu hồi quy GMM cần thiết cho mô hình như kiểm định ArellanoBond tự tương quan sai phân phần dư và kiểm định Hansen để kiểm tra có sự tương quan giữa biến công cụ và phần dư hay không.

Hầu hết các chuỗi thời gian kinh tế bao gồm các lớp phát sinh từ các khoảng thời gian đa dạng khác nhau, mỗi một mối quan hệ có thể xuất hiện trong khoảng thời gian này nhưng có thể không xuất hiện trong khoảng thời gian khác. Hơn nữa, sự cùng tồn tại của các xu hướng và chu kỳ trong chuỗi có thể che giấu hoặc bóp méo thông tin liên quan để ra quyết định. Do đó, việc không xem xét sự chuyển động của biến số ở các cấp độ theo các thang thời gian khác nhau sẽ che lấp mối quan hệ thay đổi theo thời gian của các biến số liên quan, đây được xem là vấn đề đáng quan tâm trong mối quan hệ giữa tăng trưởng – tài chính. Vì vậy, để phân tích chính xác mối quan hệ giữa CTTC và TTKT tại các khoảng thời gian khác nhau, cần có một công cụ kinh tế lượng có thể phân tách chuỗi thời gian gốc thành các chuỗi dữ liệu tại các thang thời gian khác nhau. Theo Ramsey và Lampart (1998), phép biến đổi Wavelet là một công cụ rất hữu ích trong việc điều tra mối quan hệ của các biến trên cơ sở thang thời gian khác nhau (time scale/scale – by – scale). Phân tích Wavelet cho phép phân tích đồng chuyển động và quan hệ nhân quả theo cách tiếp cận thang đo thời gian khác nhau. Vì vậy, luận án xử lý trước chuỗi dữ liệu gốc bằng phép biến đổi wavelet, phân tách chuỗi dữ liệu thành các thang thời gian khác nhau, qua đó phân tích mối quan hệ nhân quả giữa TTTC, TGTC với TTKT. Từ đó, dựa trên bằng chứng đạt được để phân tích chính xác tác động của CTTC lên TTKT tại mỗi giai đoạn phát triển kinh tế khác nhau.

3.1.2.2. Phép biến đổi Wavelet

Hai hàm Wavelet cơ bản thường được sử dụng trong phép biến đổi Wavelet là: mother wavelet, ψ và father wavelet được biểu thị theo công thức sau:

(3.38)

(3.39)

Trong đó: j = 1, ... J là tham số mở rộng trong phân rã cấp J, k là tham số dịch chuyển.

Biến đổi Wavelet rời rạc (Discrete Wavelet Transform DWT) là một kỹ thuật phân tích chuỗi thời gian có thể xử lý tính không ổn định bằng cách thực hiện kết hợp trong miền quy mô và thời gian (Daubechies, 1992). Một trong những thuật toán phổ biến nhất để tính toán DWT là phép biến đổi Wavelet rời rạc phủ toàn diện (Maximal Overlap Discrete Wavelet Transform – MODWT) vì những ưu điểm của kỹ thuật này so với DWT cổ điển, cụ thể: Thứ nhất, MODWT có thể xử lý các mẫu có kích thước N bất kỳ, trong khi DWT hạn chế kích thước mẫu thành bội số của 22, quan trọng là MODWT luôn bất biến đối với sự dịch chuyển vòng tròn của chuỗi thời gian được phân tích, trong khi DWT thì không. Hơn nữa, trong khi cả

DWT và MODWT đều có thể

được sử

dụng để

phân tích phương sai dựa trên

Wavelet và hệ số tỷ lệ, công cụ ước tính phương sai Wavelet MODWT có thể được chứng minh là tiệm cận hiệu quả hơn so với cùng một công cụ ước tính dựa trên DWT. Bên cạnh đó, ước lượng MODWT cho phép có thể xử lý chuỗi có độ dài bất kỳ. Do đó, trong luận án này, phép biến đổi MODWT được sử dụng. Trong phân tách đa phân giải của MODWT, các tín hiệu bị phân hủy theo sau:

(3.40)

Trong đó: Sj(t) và Dj(t) tương ứng với các hệ số xấp xỉ và hệ số chi tiết tương

ứng ở wavelet cấp j. Các hệ số này là thước đo sự đóng góp của hàm wavelet tương

ứng vào tổng tín hiệu cấp j. Do đó, một chuỗi thời gian y (t) có thể được biểu diễn

theo các tín hiệu theo phương trình sau:

Đồng thời, để phân rã chuỗi, bộ lọc wavelet bất đối xứng nhỏ nhất LA (8) do

Daubechies (1992) được sử

dụng, vì bộ

lọc này cung cấp sự

căn chỉnh thời gian

chính xác nhất giữa các hệ số wavelet trên một số thang đo và chuỗi thời gian gốc. Đối với phân tích đa phân giải, mức J = 2 được sử dụng, khi đó chúng ta thu được hai thành phần trực giao liên kết với một thang thời gian nhất định (D1, D2); ngoài ra còn có một thành phần dư của quá trình đại diện cho xu hướng được làm mịn (S2). Mức độ phân giải này dẫn đến ba cấp độ chi tiết: thành phần tần số cao nhất D1 đại diện cho biến động trong ngắn hạn (2 4 năm), thành phần D2 đo các biến thể theo thang thời gian 22 = 4 năm và đại diện cho các biến động trung và dài hạn (4 8 năm), S2 là phần còn lại của tín hiệu ban đầu thu được sau khi trừ D1 và D2 ra khỏi tín hiệu, đại diện cho biến động dài hạn hơn (hơn 8 năm).

Theo Hsiao (2007), lợi thế của dữ liệu bảng là giảm cộng tuyến giữa các biến giải thích và tăng bậc tự do, kiểm soát tác động của các biến bị bỏ qua và nắm

bắt các mối quan hệ

động, từ

đó cải thiện hiệu quả

cho các kiểm định kinh tế

lượng. Hơn hết, kỹ thuật dữ liệu bảng cho phép chúng ta nắm bắt được tính không đồng nhất không thể quan sát được giữa các đơn vị hay trong thời gian so với chuỗi

thời gian và đơn vị chéo. Do đó, các tham số trong ước lượng đáng tin cậy hơn trong mô hình dữ liệu bảng. Thêm vào đó, trong các dữ liệu về kinh tế và tài chính, nhiều trường hợp nếu mối quan hệ nhân quả tồn tại đối với một vùng thì cũng tồn tại đối với các vùng khác; do đó, trong những trường hợp này, mối quan hệ nhân quả có thể được kiểm tra chính xác hơn với dữ liệu bảng. Và nếu không được xử lý bằng các kỹ thuật thích hợp, có thể dẫn đến sai lệch đáng kể trong các ước lượng kinh tế lượng (Bhattacharya và cộng sự, 2016). Sự tồn tại của sự phụ thuộc chéo trong dữ liệu được giả định khi các thực thể có tính hội nhập kinh tế cao, điều này cho thấy rằng chúng nhạy cảm với các cú sốc kinh tế của các thực thể khác. Tuy nhiên, cũng có thể mỗi thực thể có động lực riêng chi phối mối quan hệ giữa CTTC và TTKT. Do đó, điều quan trọng là các kỹ thuật ước lượng mối quan hệ nhân quả bảng cần xem xét cả sự phụ thuộc chéo và tính không đồng nhất giữa các thực thể trong ước tính.

Vì vậy, luận án sử dụng kết hợp phép biến đổi Wavelet với mô hình dữ liệu bảng để phân tích mối quan hệ nhân quả giữa CTTC và TTKT tại các thang thời gian khác nhau. Kết hợp này được thực hiện như sau: Đầu tiên thực hiện phép biến đổi Wavelet để phân tách từng chuỗi trực giao và tìm ra những điểm không đồng nhất khác nhau giữa các khoảng thời gian và các quốc gia khác nhau trong mỗi chuỗi dữ liệu. Sau đó, tiến hành hồi quy bảng cho mỗi lần phân rã, lúc này mối quan hệ giữa CTTC và TTKT có thể tìm thấy tại các thang đo thời gian khác nhau và mối quan hệ nhân quả khác nhau. Theo hiểu biết của tác giả thì hiện nay chỉ có một vài nghiên cứu sử dụng phương pháp kết hợp này chẳng hạn như trong các nghiên cứu về năng lượng với tăng trưởng (Saldivia và cộng sự, 2020), tài chính toàn diện với tăng trưởng (Gourène & Mendy, 2017), năng suất với thất nghiệp (Gallegati và cộng

sự, 2016) trong khi đó vẫn chưa có nghiên cứu nào sử nghiên cứu mối quan hệ giữa CTTC và TTKT.

dụng kỹ

thuật này trong

3.1.2.3. Kiểm định nhân quả DumitrescuHurlin dữ liệu bảng

Sau khi phân tách chuỗi dữ liệu gốc thành các chuỗi dữ liệu với thàng đo thời gian khác nhau, luận án sử dụng kiểm định nhân quả của DumitrescuHurlin (2012) để phân tích mối quan hệ nhân quả giữa các biến số. Kiểm định của Dumitrescu Hurlin có ưu điểm là có thể ước lượng cả trong trường hợp T> N và N> T, và cả trong trường hợp có hoặc không có sự phụ thuộc chéo. Khi đó, kiểm định dựa trên VAR với giả định không có sự phụ thuộc chéo, ngược lại mô phỏng Monte Carlo

được sử

dụng thay thế. Kiểm định nhân quả

của DumitrescuHurlin có kết quả

mạnh trong điều kiện có sự phụ thuộc chéo với các mô phỏng Monte Carlo.

Dumitrescu và Hurlin (2012) mở

rộng phân tích mối quan hệ

nhân quả

Granger trong dữ liệu bảng theo hồi quy sau:

với i =1,…,N và t=1,…,T (3.42)

Trong đó: K là độ dài độ trễ

là một tham số tự động

hệ số hồi quy có thể thay đổi giữa các nhóm

Hệ số được phép khác nhau giữa các đơn vị nhưng được giả định là bất biến theo thời gian. Bảng phải là bảng cân bằng.

Theo Granger (1969), quy trình để xác định sự tồn tại của mối quan hệ nhân quả là kiểm định có ảnh hưởng đáng kể của các giá trị trong quá khứ của x đến giá trị hiện tại của y. Do đó, giả thuyết H0 được định nghĩa là:

Tương ứng với việc không có mối quan hệ nhân quả với tất cả các đơn vị trong bảng.

Gửi bình luận