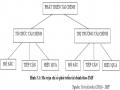
Mô Hình Nghiên Cứu Tác Động Của Phát Triển Tài Chính Lên Tăng Trưởng Kinh Tế 119718

Bảng 3.1. Các chỉ số đo lường PTTC mới

Nguồn: Tổng hợp của tác giả từ IMF và WB

Phương pháp tính bộ chỉ số PTTC mới dựa trên kết hợp phương pháp trong OECD (2008), Cámara & Tuesta (2014) và Svirydzenka (2016). Các bước lần lượt để đo lường bộ chỉ số PTTC mới theo sau:

Có thể bạn quan tâm!

Xem toàn bộ 328 trang tài liệu này.

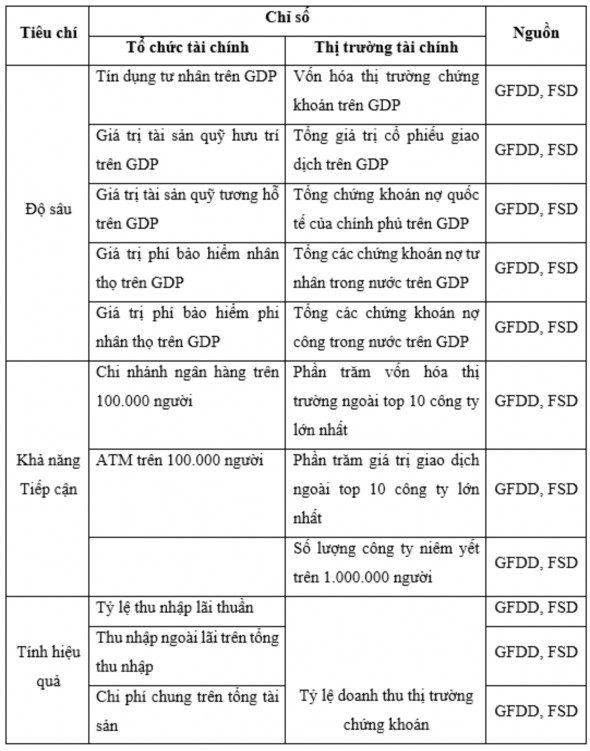
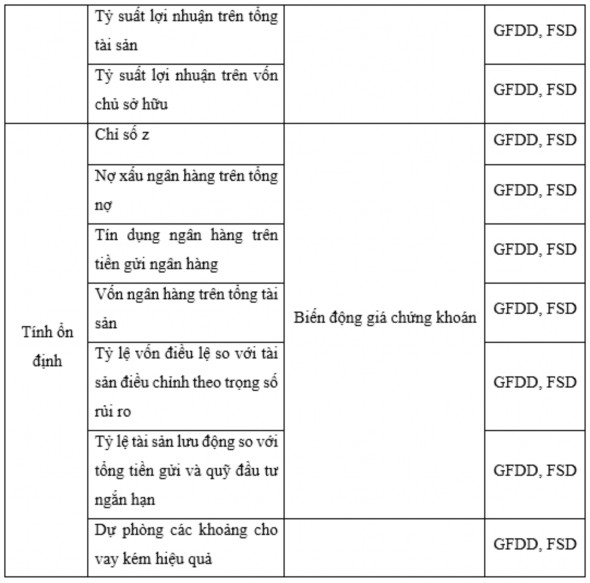
Bước 1: Các chỉ số ban đầu được winsorize để loại trừ các giá trị outlier.

Bước 2: Các chỉ số sau đó đươc chuẩn hóa theo công thức sau bằng phương pháp min – max:

(3.1)

Ngoài ra, đối với một số

chỉ

số thuộc nhóm chỉ số

hiệu quả

như: chi phí

chung trên tổng tài sản, thu nhập ngoài lãi trên tổng thu nhập và tỷ lệ thu nhập lãi

thuần, giá trị càng cao cho thấy hiệu quả hoạt động càng kém (Svirydzenka, 2016);

nhóm chỉ số thuộc nhóm tính ổn định: tín dụng ngân hàng trên tiền gửi ngân hàng, nợ xấu ngân hàng trên tổng nợ, dự phòng các khoảng cho vay kém hiệu quả và biến

động giá chứng khoán thì giá trị càng cao cho thấy tính bất ổn của hệ thống tài chính

càng cao. Do vậy đối với các chỉ

số này thì chuỗi dữ

liệu được chuẩn hóa theo

phương pháp minmax được áp dụng theo công thức sau:

(3.2)

Bước 3: Các chỉ số sau khi được chuẩn hóa, tiếp tục được tính toán thành các chỉ số phụ ở hàng dưới cùng của ma trận Hình 3.2. Mỗi một chỉ số phụ là trung bình tuyến tính có trọng số của chuỗi bên dưới với trọng số được ước tính từ phương pháp PCA.

PCA là phương pháp biến đổi giúp giảm số lượng lớn các chỉ số có tương quan với nhau thành tập ít các chỉ số sao cho các chỉ số mới tạo ra là tổ hợp tuyến tính của những chỉ số cũ không có tương quan lẫn nhau, mà vẫn giữ được nhiều nhất lượng thông tin từ các nhóm chỉ số ban đầu. Ngoài ra, trong không gian mới, có

thể giúp chúng ta khám phá thêm những thông tin quý giá mới mà tại các chiều thông tin cũ mà những thông tin này bị che mất. Theo OECD (2008), phương pháp PCA có ưu điểm là có thể tổng hợp một tập hợp các chỉ số cá nhân riêng lẽ lại với nhau trong khi vẫn bảo tồn tỷ lệ tối đa có thể của tổng biến động trong tập dữ liệu ban đầu. Phương pháp này được thực hiện bằng cách nhóm các chỉ số riêng lẻ có các hệ số tải nhân tố cao nhất thành các chỉ số tổng hợp trung gian, khi đó trọng số được xây dựng từ ma trận các hệ số tải nhân tố, bình phương các hệ số tải nhân tố thể hiện tỷ lệ của tổng phương sai đơn vị của chỉ tiêu được giải thích bởi các nhân tố. Cámara & Tuesta (2014) cho rằng một chỉ số tổng hợp tốt phải bao gồm thông tin

quan trọng từ

tất cả

các chỉ

số, nhưng không được thiên vị

mạnh về

một hoặc

nhiều chỉ số. Khi đó, phương pháp PCA hai giai đoạn phù hợp để tính toán bộ chỉ số PTTC mới. Trong giai đoạn đầu, luận án ước tính các chỉ số phụ của TCTC (FID, FIA, FIE, FIS) và TTTC (FMD, FMA, FME, FMS). Giai đoạn thứ hai, luận án ước tính trọng số của từng chỉ số và tính toán các chỉ số FI, FM và chỉ số tổng hợp cuối

cùng FD. Khi đó, phương trình chung để pháp PCA là:

tính toán các chỉ

số PTTC theo phương

(3.3)

Trong đó: i biểu thị cho quốc gia; FDLI là đại diện cho mười một chỉ số PTTC bao gồm:

FD – Chỉ số PTTC tổng hợp FI – Chỉ số PTTC của TCTC FM – Chỉ số PTTC của TTTC

FID – Chỉ số PTTC với khía cạnh độ sâu tài chính TCTC

FIA – Chỉ số PTTC với khía cạnh khả năng tiếp cận của TCTC FIE – Chỉ số PTTC với khía cạnh tính hiệu quả của TCTC

FIS – Chỉ số PTTC với khía cạnh tính ổn định của TCTC FMD – Chỉ số PTTC với khía cạnh độ sâu tài chính của TTTC

FMA – Chỉ số PTTC với khía cạnh khả năng tiếp cận của TTTC FME – Chỉ số PTTC với khía cạnh tính hiệu quả của TTTC FMS – Chỉ số PTTC với khía cạnh tính ổn định của TTTC

Theo Svirydzenka (2016), các chỉ số phụ đại diện cho TCTC và TTTC được tính toán dựa trên phương pháp PCA theo phương trình sau:

(3.4)

Trong đó:

(3.5)

wka, wmb: trọng số riêng lẽ khác nhau của từng chỉ số phụ đại diện cho

TCTC và TTTC

FIj: lần lượt đại diện cho các biến của TCTC là FID, FIA, FIE và FIS

FMj: lần lượt đại diện cho các biến của TTTC là FMD, FMA, FME và FMS Các chỉ số phụ được xây dựng dưới dạng giá trị trung bình có trọng số của

chuỗi được chuẩn hóa, trong đó trọng số là hệ số tải bình phương (sao cho tổng của chúng cộng lại bằng 1) từ phân tích thành phần chính của chuỗi cơ sở. Hệ số tải nhân tố là hệ số liên quan giữa các biến quan sát với các thành phần chính hoặc các nhân tố. Bình phương tải nhân tố thể hiện tỷ lệ của tổng phương sai đơn vị của chỉ tiêu được giải thích bởi nhân tố. Chuỗi đóng góp nhiều hơn vào hướng biến đổi chung trong dữ liệu sẽ có trọng số cao hơn. Trọng số chỉ can thiệp để điều chỉnh thông tin trùng lặp giữa hai hoặc nhiều chỉ số tương quan và không phải là thước đo tầm quan trọng lý thuyết của chỉ số liên quan.

Bước 4: Các chỉ số tiếp tục chuẩn hóa lần nữa để giữ cho các chỉ số luôn nằm giữa 0 và 1;

Bước 5: Các chỉ số tiếp tục được tổng hợp thành chỉ số tổng hợp cao hơn theo quy trình tương tự từ bước 1 đến bước 4. Các chỉ số PTTC tổng hợp được xây dựng theo phương trình sau:

(3.6)

(3.7)

(3.8)

Trọng số để xây dựng chỉ số FD tổng hợp cuối cùng được tính theo công thức

(3.9)

Trong đó: là phương sai của thành phần chính thứ j, là các giá trị riêng của ma trận tương quan của các chỉ số phụ.

Về xử lý dữ liệu bị thiếu, Svirydzenka (2016) IMF đề xuất xử lý bằng một số cách như: nếu dữ liệu năm sau bị thiếu thì sẽ sử dụng dữ liệu của năm trước đó thay thế, coi dữ liệu là thực sự bị thiếu, loại trừ chuỗi khỏi chỉ số trung bình khi dữ liệu không có sẵn; coi dữ liệu là 0, giả định rằng việc không có dữ liệu có nghĩa là thị trường này không tồn tại hoặc tính hiệu quả và khả năng tiếp cận của thị trường rất kém; ghép hai chỉ số trước và sau của chuỗi dữ liệu lại với nhau. Tuy nhiên, có thể thấy rằng việc loại trừ chuỗi dữ liệu khỏi chỉ số trung bình hay đánh đồng dữ liệu bằng 0 xem như thị trường này tính hiệu quả và khả năng tiếp cận rất kém là

không hợp lý. Do đó, trong luận án này tác giả dựa vào thuật toán K – Nearest Neighbour (KNN) để xử lý vấn đề bị thiếu dữ liệu, với các giả định là những dữ

liệu tương tự

nhau sẽ

tồn tại gần nhau trong một không gian. Một trong những

điểm hữu ích của KNN là thuật toán này chỉ dựa trên khoảng cách giữa điểm dữ liệu cần phân loại Kowarik và Templ (2016).

3.1.1.2. Mô hình nghiên cứu tác động của phát triển tài chính lên tăng trưởng kinh tế

Đầu tiên, luận án xây dựng mô hình kinh tế lượng dữ liệu bảng cơ bản tác động của PTTC lên TTKT dựa trên nền tảng lý thuyết tăng trưởng nội sinh được phát triển bởi King và Levine (1993) theo sau:

(3.10)

Trong đó:

FDLI bao gồm bộ mười một chỉ số PTTC.

Z là nhóm các biến kiểm soát: TRADE, GROSS, POP. GROWTH: tăng trưởng kinh tế.

Dựa theo nghiên cứu của Pesaran và cộng sự (1999), Loayza và Ranciere

(2006), Samargandi và cộng sự (2015), để phân tích tác động tuyến tính của PTTC lên TTKT, mô hình (3.10) có thể được ước lượng dựa trên PARDL như sau:

(3.11)

Trong đó: X là nhóm các biến FDLI và các biến Z.

Nếu các biến trong phương trình 3.11 có mối quan hệ đồng liên kết với nhau và sai số là một tiến trình I(0) với mọi i, khi đó phương trình hiệu chỉnh sai số của phương trình 3.11 được tham số hóa lại như sau:

(

3.12)

Trong đó:

j= 1,2,….., p1

j= 1,2,…., q1

Tham số là tốc độ hiệu chỉnh sai số, nếu không có bằng chứng mối quan hệ dài hạn. Tham số này được kỳ vọng là âm và có ý nghĩa thống kê với giả định là các

biến quay trở lại trạng thái cân bằng trong dài hạn.

Mô hình ARDL ưu việc hơn các mô hình kiểm định đồng liên kết khác bởi hai lý do như sau: Thứ nhất, mô hình này không yêu cầu số mẫu lớn như các kỹ thuật đồng liên kết khác, do đó việc kiểm định đồng liên kết với mẫu nhỏ áp dụng kỹ thuật ARDL là thích hợp hơn; Thứ hai, mô hình ARDL được ưu thích hơn so với các phương pháp đồng liên kết khác khi xử lý các biến có độ trễ khác nhau, với các bậc sai phân khác nhau I(0) với I(1) hoặc toàn bộ là I(0) hoặc I(1). Mô hình PARDL

Gửi bình luận