Biện Pháp 3: Rèn Luyện Cho Học Sinh Năng Lực Phát Hiện Vấn Đề Và Khám Phá Tri

Cách giải theo hình thức tự luận

Ta có: a  log 3  1  log 2  1 và log 5  1

log3 2 a b

log 45

log3 3 .5

2  log 5 2 b

a  2ab

Vậy: log 45 3 3 

log3 6 log3 3.2

1  log32 1 1

ab  b

Cách giải có ứng dụng máy tính cầm tay

- Nhập vào màn hình log23 rồi lưu và A

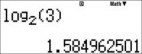
- Nhập vào màn hình log53 rồi lưu vào B

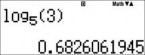
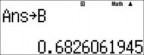
- Bắt đầu kiểm tra tính đúng sai của đáp án A. Nếu đáp án A

đúng thì hiệu log 45  a 2ab

phải bằng 0.

6 ab

Ta nhập hiệu trên vào máy tính cầm tay và bấm nút =

- Kết quả hiển thị của máy tính Casio là 1 giá trị khác 0 vậy đáp án A sai.

- Tương tự như vậy ta kiểm tra lần lượt từng đáp án và ta thấy

hiệu

log 45  a 2ab

bằng 0

6ab  b

Vậy log 45  a 2ab

hay đáp án C là đúng.

6ab  b

Ví dụ 2.7 : Tìm tập nghiệm S của phương trình

x2 2 x3



2 8x

A. S  1;3.

B. S  1;3.

C.S  3;1.

Giải

D.S  3.

Chuyển sang vế trái nhập vào máy tính:

x2 2 x3



2 8x

CALC	1	=

CALC	3	=

Có thể bạn quan tâm!

Xem toàn bộ 140 trang tài liệu này.

Được kết quả là 0 ( nhận)

Được kết quả là 0 ( nhận). Vậy đáp án là A

Ví dụ 2.8: Tìm tập nghiệm của: log

x1 log1x 1 1.

A.S  3  13.

B. S  3.







C. S  2 



2 

5; 2 

5.

Giải

D. S  2 

5.

Chuyển sang vế trái nhập vào máy tính: log

x1 log1x 1 1.

CALC

3  1 3 / 2

CALC

2  5

Ví dụ 2.9: Tìm số nghiệm của: log

Khác 0 ( loại A) Khác 0 ( loại B)

Khác 0 ( loại C). Vậy đáp án là D

x 5  log (x2 25)  1

2 x 5 2

A. 2 B. 1 C. 0 D. Vô số nghiệm

Giải

+ Nhập

log

x 5  log (x2 25) 1

2 x 5 2

SHIFT

SOLVE

+ Được nghệm x = 6,….

SHIFT

STO

Sau đó lưu vào A

+ Nhập

log x 5 log (x225) 1 X A

 2 x 5 2 

 

SHIFT

SOLVE

-6

SHIFT

SOLVE

Ta thấy cả hai lần này L-R khác 0. Nếu L –R khác 0 thì nghiệm đó không phải là nghiệm của phương trình, nghiệm thứ 2 của phương trình này nếu có sẽ khác nghiệm thứ nhất và L- R bằng 0. Vậy phương trình có duy nhất 1 nghiệm. Chọn đáp án B.

Ví dụ 2.10: Tính đạo hàm các hàm số sau:

A. 3sin x  cos xe2x

C.3sin x  cos xe2x

y  (sin x  cos x)e2x

B. 3sin x  cos xe2x

D.3sin x  cos xe2x

Giải

Cách 1: dùng công thức

a) y  (sin x  cos x)e2x

y '  (cos x  sin x)e2x 2sin x  cos xe2x 3sin x  cos xe2x

Cách 2: Bấm máy tính

Bước 1:

d(sin x  cos x)e2x  dx

x3

= Kq 570,187

Bước 2: bấm biểu thức vào máy: (3sin x  cos x)e2x

sau đó bấm

CALC

Kết qủa 570,187. Chọn A Để giải được bài toán này, học sinh phải biết sử dụng các công thức

tính đạo hàm của hàm số mǜ, lôgarit ngoài ra còn phải nắm chắc các quy tắc tính đạo hàm của một tích, một thương, … Ngoài ra còn phải biết rút gọn các biểu thức lượng giác, mǜ, logarit,…

Ví dụ 2.11: Một người gửi 50 triệu đồng vào một ngân hàng với lãi suất

6% / năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm

số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 100 triệu đồng bao gồm cả gốc và lãi? Giả sử trong suốt thời gian gửi lãi suất không đổi và người đó không rút tiền ra.

A. 13 năm. B. 12 năm. C. 14 năm. D. 11 năm.

Giải

Cách 1: A= a(1+r%)n, sau đó lấy logarit, tìm được n. Đáp án B.

Cách 2: nhập 50 -100(1+6%)x vào máy tính. Sau đó CALC các đáp án vào máy tính. Kết quả 12 máy tính bằng 0. Đáp án B

Ví dụ 2.12: Tập nghiệm của bất phương trình:

2019

x23 x 1 2019x2 

 x  3  0 là

x2 3x

A. ; 0

B. C. 3

Giải

D. 3; 

Cách 1:Giải theo cách tự luận rất dài và khó

- Học sinh giải điều kiện cho căn bậc hai

x2 3x

- Học sinh giải bất phương trình. Lấy giao: được kết quả là C

Cách 2: nhập vào máy tính 2019

x23 x 1 2019x2 

 x  3

CALC

Được kết quả 0 nhận. Sau đó CALC số 4 dương loại D.

2 2

CALC số -1 dương loại A. Đáp án đúng là C Ví dụ 2.13: Tập nghiệm của : 3sin x1  3cos x1 x213x 2x1  4x  9

A. ; 0

B. C. 3

D. ; 

Ví dụ 2.14: Số nghiệm của phương trình 2.4x 9x1  11.6x

A. 0 B. 1 C. 2 D. 3

Giải

Cách 1: Giải theo cách tự luận

- Học sinh chia 2 vế cho 4x hoặc 9x

- Học sinh giải tìm x được 2 nghiệm là x = 0; Kết quả là C

x  log

 2 

3 9

 

2  

Cách 2: MODE 7 nhập vào máy tính

f (x)  2.4x 9x1 11.6x

START

-9

END

STEP

Được 2 vùng f(x) dương, 1 vùng f(x) âm. Kết luận có 2 lần f(x) đổi dấu.

Kết quả f(x) = 0 có 2 nghiệm. Đáp án C

Ví dụ 2.15: Có bao nhiêu giá trị nguyên dương của tham số để phương trình

16x 2.12x (m  2)9x 0

có nghiệm dương?

A. 1. B. 2 . C. 4 . D. 3 .

Giải Cách 1:Giải theo cách tự luận

- Học sinh chia 2 vế cho .16x . hoặc 9x

- Học sinh giải tìm được 2 giá trị m. Kết quả là B Cách 2:

- Học sinh đưa phương trình về :

2.9x 2.12x16x

m 

- GV: Nếu m = f(x) các em dự kiến sử dụng máy tính thế nào?

- HS: có thể tìm miền giá trị của f(x)

- GV: Tìm miền giá trị cách nào hiệu quả nhất?

- HS: dùng mode 7

- HS bấm MODE 7 nhập vào máy tính

f (x) 

2.9x 2.12x16x

START

-9

END

STEP

Ta thấy được f(x) dương thuộc vùng nghiệm (0,2; 2,9). Vậy m = 1 và m = 2. Đáp án B.

2.2.3. Biện pháp 3: Rèn luyện cho học sinh năng lực phát hiện vấn đề và khám phá tri thức một cách sáng tạo

2.2.3.1. Mục đích biện pháp

- Giúp học sinh phát hiện vấn đề và khám phá tri thức một cách sáng tạo từ các bài tập.

- Tổ chức hoạt động khám phá cho học sinh trong dạy học nhằm nghiên cứu nhằm góp phần phát huy tính sáng tạo, tự học, năng lực tự nghiên cứu cho học sinh, nâng cao chất lượng học tập toán ở trường THPT.

2.2.3.2. Cách thức thực hiện

A. Tổ chức cho học sinh phát hiện, khám phá các qui tắc thuật giải, tựa thuật giải

Trong quá trình học chủ đề phương trình, bất phương mǜ và logarit học sinh được hình thành nhiều qui tắc hoặc các bước thực hiện giải bài tập toán như: qui tắc biến đổi, các phương pháp giải phương trình, bất phương trình.

Những qui tắc, trình tự thực hiện trên hầu hết là các thuật giải hoặc tựa thuật giải. Như vậy việc hình thành các thuật giải và tựa thuật giải chiếm một vị trí quan trọng trong trong giải phương trình, bất phương trình mǜ và logarit. Cho nên việc tổ chức cho học sinh khám phá ra các qui tắc, trình tự thực hiện trong bài học cần được quan tâm đúng mức, từ đó sẽ góp phần nâng cao hiệu quả và tích cực hóa hoạt động học của học sinh.

B. Khám phá cách giải bài tập phương trình, bất phương trình mǜ và logarit thông qua việc phát hiện, sửa chữa sai lầm trong giải toán

Sai lầm khi sử dụng phương pháp đưa về cùng cơ số (Do HS áp dụng sai định lý, tính chất, định nghĩa).

2.2.3.3 Các ví dụ minh họa:

Ví dụ 2.16: Khám phá tựa thuật toán để phát hiện vấn đề từ phương pháp đặt ẩn phụ

Bài tập 1. Giải các phương trình sau:

a) 22x  3.2x 2  0 b) 25x 6.5x 5  0

Định hướng cách giải bài toán:

Với câu a thì học sinh dễ dàng giải quyết được bài toán bằng cách đặt

t  2x ,t  0 nhưng với câu b sẽ khó khăn hơn nhiều nếu áp dụng theo cách

giải của câu a. Khi học sinh gặp khó khăn giáo viên định hướng cho sinh bằng câu hỏi: Làm như thế nào để đưa bài về dạng như câu a? Với gợi ý như thế học sinh phát hiện cách giải bài toán bằng cách đưa hàm số về cùng cơ số 5.

* Giáo viên hướng dẫn học sinh mô tả, xây dựng các bước giải câu b.

Bước 1: Biến đổi 25x về mǜ với cơ số 5.

Bước 2: Đặt ẩn phụ t  5x ,t  0 ta được phương trình bậc hai theo t.

Bước 3: Giải phương trình theo t và so sánh với điều kiện. Bước 4: Giải phương trình mǜ cơ bản.

Sau đó giáo viên có thể cho học sinh giải các bài tập ở bài tập 2 để nâng dần mức độ khó khăn của dạng toán này.

Bài tập 2. Giải các phương trình sau:

2 2

a) 72x 1  8.7x 1  0 b) 9x x1 10.3x x2  1  0

* Từ các ví dụ trên giáo viên có thể định hướng cho học sinh khám phá tựa thuật giải cho bài toán tổng quát sau:

Bài toán: Xét phương trình

m, n, p  R

m.a2f ( x )  n.a f( x )  p  0

với 0  a  1 và

Bước 1: Đặt ẩn phụ t  a f( x ) ,t  0 . Khi đó ta có: m.t2 n.t  p  0 . Bước 2: Giải phương trình theo t và so sánh với điều kiện của t.

Bước 3: Đưa về phương trình mǜ cơ bản và ta giải phương trình tìm x.

Ví dụ 2.17: Khám phá thuật giải phương trình dạng:

m.a f( x )  n.(ab) f( x )  p.b f( x )  0 với 0  a  1 và m, n, p  R

Giải phương trình: a) 52x  10x 2.22x

2 2 2

b) 32 x 6 x 9 4.15x 3 x5 3.52 x 6 x9

Giáo viên định hướng học sinh giải phương trình như sau:

GV: Đưa phương trình về dạng quen thuộc là đưa biến đổi cùng số mǜ. HS: 25x 10x 2.4x

Gv: Đưa về cùng cơ số.

HS: Chia cả hai vế của phương trình cho 4x hoặc 25x (dưới sự hướng dẫn

 25 x 5x

của giáo viên).  4 

  2

 2 .

   

GV: Ta đã gặp dạng nào tương tự?

Đến đây học sinh có thể giải quyết bài toán một cách dễ dàng. Từ đó, dưới sự dẫn dắt của GV, học sinh quát thành thuật toán giải phương trình trên:

Bước 1: Chia cả hai của phương trình cho b f ( x )hay a f ( x ) . Bước 2: Đưa về cùng cơ số.

Bước 3: Đặt ẩn phụ theo t và giải phương trình theo t

Bước 4: Giải phương mǜ cơ bản để tìm x.

Ví dụ 2.18: Khám phá phát hiện vấn đề của một số bài toán lãi suất:

Bài tập 1: Lãi suất đơn

Anh X gửi vào ngân hàng 10 triệu đồng với lãi suất đơn 7%/năm thì sau 5 năm số tiền thầy A nhận được cả vốn lẫn lãi là bao nhiêu?

A.13,5 triệu B. 16 triệu C.12 triệu D.12,7triệu

Giải

Khách hàng gửi vào ngân hàng A đồng với lãi suất đơn r%/kì hạn thì số

tiền khách hàng nhận được cả vốn lẫn lãi sau n kì hạn n  N *

SnA1 n.r%

Chú ý trong các bài toán lãi suất cà các bài toán liên quan, r%

là: