- HS:
y x2
3x 2
2019 x2020
x1 ;
2019x 2020
x 1
Có thể bạn quan tâm!
-
Các Thành Tố Về Năng Lực Tính Toán Của Chương Ii Giải Tích 12 -
Thực Trạng Dạy Học Phát Triển Năng Lực Tính Toán Chương Ii Hàm Số Lǜy Thừa, Hàm Số Mǜ Và Hàm Số Lôgarit Cho Học Sinh Ở Một Số Trường Phổ Thông -
Các Biện Pháp Phát Triển Năng Lực Tính Toán Cho Học Sinh Thông Qua Hoạt Động Dạy Bài Tập Hàm Số Lǜy Thừa, Hàm Số Mǜ Và Hàm Số Logarit -
Biện Pháp 3: Rèn Luyện Cho Học Sinh Năng Lực Phát Hiện Vấn Đề Và Khám Phá Tri Thức Một Cách Sáng Tạo -
0 Là Âm Có Tần Số 1000Hz (Ứng Với Cường Độ Âm -
Phát triển năng lực tính toán cho học sinh trong dạy học bài tập hàm số lũy thừa, hàm số mũ và hàm số logarit giải tích 12 trung học phổ thông - 10
Xem toàn bộ 140 trang tài liệu này.
không nguyên
x2 3x 2 0
x 2
x 2
Nên
x 1 0
x 1 x 1
x 1
Vậy tập xác định của hàm số là
D ;1 2;
B) - GV: Hàm
y log x2 3x 1ta tìm TXĐ như thế nào?
- HS: y loga x có điều kiện x > 0 và 0 < a ≠ 1
x 2 0
Ta có: x 2 0
x 2
x 2 x 1
.Vậy TXĐ là:
D 1 ;
3
3
3x 1 0 1
x
3
C) - GV: Tìm TXĐ như thế nào?
- HS:
Biểu thức trong căn bậc hai lớn hơn hoặc bằng 0 và
x 2 >0
x 2
Ta có:
log
x 20
2
1x 2
x 21
x 2
x 21 0
x 2
x 20
x 2
x 2
x 20
x 2
x 2
x 2
x 2 x 2
x 2
Vậy tập xác định của hàm số là:
D 2;
Đối với phương trình, bất phương trình mǜ và lôgarit thường liên quan đến đặt điều kiện cho ẩn phụ chứa hàm số mǜ hay đặt điều kiện cho biểu thức
bên trong lôgarit hoặc đặt điều kiện của cơ số có chứa tham số thường học sinh không chú trọng nân ta cần tạo cho học sinh thói quen đặt điều kiện này. Ví dụ 2.3: Sử dụng công thức để so sánh, rút gọn hay tính giá trị biểu thức: Bài tập 1: So sánh 2 số sau:
1
a) log3 4 và l og4 3
log 1,1 log 0,99
6 4
b) 3 và 7
Nhận xét: Đối với dạng so sánh hai lôgarit cần lưu ý học sinh phân chia các trường hợp
- Nếu so sánh hai lôgarit có cùng cơ số thì chú ý đến cơ số trong hai trường hợp (0;1) và lớn hơn 1 để so sánh hai biểu thức bị lôgarit hóa với nhau.
- Trong trường hợp hai lôgarit khác cơ số, khác biểu thức bị lôgarit hóa thì ta chọn một số b nào đó. Sau đó ta so sánh hai lôgarit với số b.
Từ đó suy ra kết quả.
Giải
Cách 1:
- GV: So sánh các em cần sử dụng công thức nào?
- HS:
aloga x x
và am an a 1
m n
- GV: Các em so sánh như thế nào?
- HS:
6 6
log 1,1 log 1
*
log40,99
log61 log61,1
log40,99
3 3
1;7
7 3 7
* log34 > log33 = 1; log
1 log 4 1 log 4 log 1
4 3 4 3 4 3
Cách 2: Có thể hướng dẫn cho HS sử dụng máy tính như sau:
1
a) log3 4 - l og4 3
log 1,1 log 0,99
6 4
> 0 b) 3 - 7 > 0
Bài tập 2: Rút gọn biểu thức sau:
A= 36log65 8log23 101log102 2019
Giải
- GV: chúng ta sử dụng công thức lǜy thừa nào?
- HS:
alogab b ; log b log b ; (am)n am.n (an)m
a a
- GV: Biến đổi như thế nào, dùng công thức nào trước?
- HS: (am )n am.n (an )m
- GV đặt câu hỏi tiếp: Bạn nào thực hành biế rút gọn ?
Hướng dẫn lời giải: 36log 5 8log 3 101log 2
62log 5 23log 3 10
6 2
Vậy A = -2016
10 6 2
10log10 2
6log65 22log23 3103
2
5
a b c
Bài tập 3: Cho loga x 2, logb x 3,logc x 4 . Tính giá trị của biểu thức: log 2x
A. 12 13
B. 1 9
C. 6 13
D.24
7
Giải
Cách 1: - GV: Bài toán cần dùng công thức liên quan nào?
- HS:
log
b 1 log
b ; log (b.c) log b log c ; log b log b ;
a a
a a a a a
- GV: Biến đổi như thế nào, dùng công thức nào trước?
- HS: log
b 1 log b
a a
- GV: Bạn nào thực hành rút gọn ? Hướng dẫn lời giải:
log
Đề có : log
log
x 2 log
a x
b x 3 logx c x 4 logx
a 1
2
b 1
3
c 1
4
log
a2b c
x5 5log x 5 1 5
x x
1
1
2 1
x
a .b.c2
log (a2 .b.c2 )
2 log
a log b
log c
2 x
5
2 1 1 1 . 1
2 3 2 4
= 24
7
Cách 2: Ngoài ra GV có thể hướng dẫn cho học sinh dùng máy tính để kiểm tra kết quả như sau:
Chọn x =2; a2 x a
2;b 3 2;c . Sau đó nhập
4 2
log
2 3 2 4 2
25
=
Kết quả được 24 . Chọn D
7
ab2 ab1 2a3b3
x2 yx2 y1
3
Bài tập 4: Giá trị của biểu thức là:
A.
Cách 1:
a8b2
B. a2b8
C. a8
Giải
D. a8 .b
- GV: chúng ta sử dụng công thức liên quan nào?
- HS:
a n 1
an
a
alogab b
a .a
a
a
a
a
a
(ab) a .b
b
b
(am )n am.n (an )m
- GV: Bạn nào thực hành biến đổi rút gọn ?
Hướng dẫn lời giải:
2
1 2 1 1 3 1
ab2 ab1 a3b3
a .a .b
2
2
3
.
a2ba2b1 3
b b a b a8 .b
1.b. 1. 1 1
a2 a6 b3 a8b2
+ Sử dụng các công thức rút gọc được đáp án D
Cách 2:
Nhập vào máy tính
ab2 ab1 2a3b3 x2 yx2 y1 3
2
=
3
=
CALC
Sau đó bấm
Được kết quả : 768
Sau đó thế a = 2; b = 3 vào 4 đáp án. Chọn kết quả D có kết quả là 768
2.2.2. Biện pháp 2: Rèn luyệncho học sinh biết sử dụng máy tính cầm tay để kiểm tra lại đáp số
2.2.2.1. Mục đích biện pháp
- Giúp học sinh kiểm tra nhanh đáp án cho bài toán tự luận.
- Giúp học sinh có hướng đi mới để giải nhanh bài tập trắc nghiệm.
2.2.2.2. Cách thức thực hiện
Sau khi học sinh giải toán theo hình thức tự luận xong, giáo viên dành ít phút cho học sinh tự kiểm tra lại đáp án bằng máy tính cầm tay hoặc định hướng cho học sinh sử dụng các phím chức năng nào để kiểm tra lại đáp án.
Cho học sinh giải toán hình thức trắc nghiệm theo đề thi minh họa của kì thi THPT Quốc gia.
Định hướng học sinh phân loại các dạng toán nào có thể vận dụng máy tính cầm tay để tìm nhanh đáp án.
2.2.2.3 Các ví dụ minh họa
1
Ví dụ 2.4: Bất phương trình log
log
3
2x 1 0
x 1
có tập nghiệm là:
A. ;2
C. 2;1 1;4
2
B. 4;
D. ; 2 4;
Cách giải theo hình thức tự luận
log log
2x 1 log 1
1 3 x 1 1
2
2 log
2x 1 1
2x 1
3x 1
x 1 0 2x 1
log
log 1
log3
2x 1 0
x 1
3
x 1 3
log
2x 1 log 3
2x 13
x 40
3 x 1
3
x 1
x 1
2x 1
1
2x 1
0
x 1
x 1
x 1
x 2
x 4
x 1
x 1
x 2
x 4
x 2
Cách giải có ứng dụng máy tính cầm tay
PHƯƠNG PHÁP 1: CALC THEO CHIỀU THUẬN
Bước 1: Chuyển bài toán bất phương trình về bài toán xét dấu bằng cách chuyển hết các số hạng về vế trái.
Khi đó bất phương trình sẽ có dạng vế trái 0 hoặc vế trái 0
Bước 2: Sử dụng chức năng CALC của máy tính Casio để xét dấu các khoảng nghiệm từ đó rút ra đáp số đúng nhất của bài toán.
CALC có nội dung: Nếu bất phương trình có nghiệm tập nghiệm là khoảng (a;b) thì bất phương trình đúng với mọi giá trị thuộc khoảng (a;b)
Nhập vào vế trái : log
log
3
2x 1
x 1
1
2
Sau đó CALC một số giá trị( 3 đến 5 giá trị) của vùng
; 2 4; đáp án D thỏa mãn đề bài.
PHƯƠNG PHÁP 2: LẬP BẢNG GIÁ TRỊ MODE 7
Bước 1: Chuyển bài toán bất phương trình về bài toán xét dấu bằng cách chuyển hết các số hạng về vế trái.
Khi đó bất phương trình sẽ có dạng vế trái 0 hoặc vế trái 0
Bước 2: Sử dụng chức năng lập bảng giá trị MODE 7 của máy tính cầm tay để xét dấu các khoảng nghiệm từ đó rút ra đáp số đúng nhất của bài toán.
* Chú ý: Cần làm nhiều bài toán tự luyện để từ đó rút ra kinh nghiệm thiết lập Start; End; Step hợp lý.
Vào MODE 7 và nhập vế trái vào máy tính
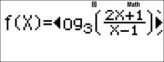
Quan sát các cận của đáp số là -2;4;1 nên ta phải thiết lập miền gia 1trị của x sao cho x chạy qua các giá trị này. Ta thiết lập Start – 4 End 5 Step 0.5
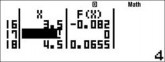
Quan sát bảng giá trị ta thấy rò ràng hai khoảng ; 2 và 4;
làm cho dấu vế trái dương. => Đáp án chính xác là D
5 3x 3x
Ví dụ 2.5: Cho 9x + 9-x = 23. Khi đó
P 1 3x 3x
có giá trị là
A. 2 B. 3
2
Cách giải theo hình thức tự luận
C. 1 2
D. 5
2
Đặt t 3x 3x t 2 9x 9x 2 25 t 5
Vì t 3x 3x 0
nên t = 5 thế vào P ta được
P 5 5 5
1 5 2
Cách giải có ứng dụng máy tính cầm tay
Bước 1: Dựa vào hệ thức điều kiện của đề bài chọn giá trị thích hợp cho biến.
Bước 2: Tính các giá trị liên quan đến biến rồi gắn vào A, B, C nếu các giá trị tính được lẻ
Bước 3: Quan sát 4 đáp án và chọn đáp án chính xác.
Áp dụng vào ví dụ 2.5
Từ Phương trình điều kiện ta có thể dò được nghiệm bằng chức năng SHIFT SOLVE.
Lưu nghiệm này vào giá trị A
Để tính giá trị biểu thức P ta chỉ cần gắn giá trị x= A sẽ được giá trị P
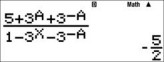
Vậy đáp án đúng là D
Ví dụ 2.6: Đặt a log2 3; b log5 3. Biểu diễn log6 45 theo a và b.
A. log6 45
6
C. log 45
a 2ab ab
a 2ab ab b
B. log6 45
D. log6 45
2a2 2ab ab
2a2 2ab ab b