Với nhiệm vụ dự đoán lí do cho câu trả lời của HS điều này thể hiện khả năng của các GVTTL hiểu sâu sắc về cách thức HS tư duy khi học về độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram.
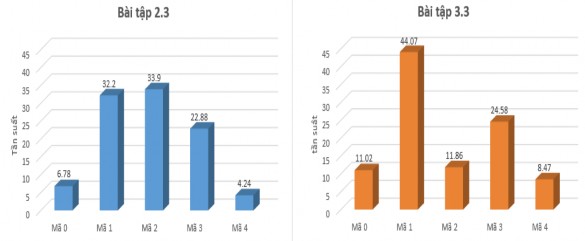
Hình 5.14. Biểu đồ biểu diễn dữ liệu về SCK32 của GVTTL trong thực nghiệm 3 Kết quả của bài tập 2.3 và 3.3 thể hiện ở hình 5.13 cho thấy tỉ lệ các GVTTL
có thể dự đoán cho các câu trả lời của HS (mã 4) ở cả hai trường hợp rất thấp. Phần
lớn các GVTTL chỉ đạt mã 1 và 2 tức là chỉ đưa ra dự đoán đúng cho câu trả lời của một HS hoặc có phản hồi cho câu hỏi nhưng không chính xác. Điều này cho thấy một số GVTTL vẫn chưa hiểu được cách thức HS lập luận hay đưa ra bằng chứng kiến thức cho câu trả lời của HS.
Từ những phân tích ở trên cho thấy kiến thức nội dung đặc thù dành cho việc dạy học độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram của các GVTTL đang còn rất hạn chế. Bên cạnh đó, kết quả cũng chỉ ra rằng cho dù các GVTTL có kiến thức toán về nội dung giảng dạy tốt cũng không thể khẳng định rằng họ có SCK dành cho việc dạy học sẽ tốt.
b) Sự tiến triển kiến thức nội dung đặc thù của giáo viên toán tương lai để dạy học độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram qua nghiên cứu bài học
Tiếp nối hai bài học trước, nghiên cứu cho thấy việc tham gia vào NCBH thứ ba thúc đẩy sự phát triển SCK theo hai yếu tố chính là: nâng cao nhận thức về cách xác định phương án trả lời khác nhau cho một nhiệm vụ cụ thể góp phần phát triển sự hiểu biết sâu hơn về độ phân tán của dữ liệu được biểu diễn trên biểu đồ cột và
biểu đồ histogram và phát triển chuyên môn trong việc xác định bản chất và nguồn gốc của các sai lầm kiến thức của HS. Sự phát triển SCK của những người tham gia được thể hiện qua các thảo luận các bước lên kế hoạch bài học. Các GVTTL cùng trao đổi về bài tập 2.2 và dự đoán lí do đưa ra câu trả lời của các HS.
Ở bài tập 2.2, HS 2 trả lời đúng vì biết đánh giá độ phân tán của dữ liệu qua phương sai, độ lệch chuẩn. HS 1 trả lời sai vì độ phân tán không phải được đánh giá bởi lượng mưa của các tháng. Lí do HS trả lời như vậy là cho rằng vùng A có nhiều số tháng có lượng mưa lớn hơn thì sẽ có độ phân tán nhiều hơn. | |
GVTTL H09: | Vậy, HS 3 và HS 4 đều trả lời sai. Vì sao họ lại đưa ra câu trả lời như vậy? |
GVTTL H34: | HS 3 nhầm lẫn việc so sánh độ phân tán của lượng mưa là so sánh lượng mưa trung bình. Còn HS 4 nghĩ rằng phải có số liệu cụ thể để tính toán thì mới so sánh được. HS 4 chưa biết cách so sánh độ phân tán dựa vào hình dáng của biểu đồ cột. |
Có thể bạn quan tâm!
-
Minh Họa Phản Hồi Của Gvttl D40 Về Sck Trong Phiếu Phỏng Vấn Bảng 5.7 Mô Tả Các Kiểu Kiến Thức Để Dạy Học Biểu Đồ Cột Và Biểu Đồ Histogram -
Sự Tiến Triển Kiến Thức Về Việc Học Của Học Sinh Của Giáo Viên Toán Tương Lai Để Dạy Học Các Số Đặc Trưng Đo Xu Thế Trung Tâm Trên Biểu Đồ -
Hình Các Gvttl Thực Hiện Tiết Dạy Trên Lớp Thực Nghiệm -
Sự Tiến Triển Tiến Triển Kiến Thức Để Dạy Học Độ Phân Tán Của Dữ Liệu Trên Biểu Đồ Cột Và Biểu Đồ Histogram Của Gvttl Qua Nghiên Cứu -
Những Đề Xuất Về Đổi Mới Đào Tạo Nghiệp Vụ Cho Giáo Viên Toán Tương Lai Hiện Nay -
Phát triển kiến thức và thực hành nghiệp vụ của giáo viên Toán tương lai để dạy học thống kê - 21
Xem toàn bộ 277 trang tài liệu này.
Bên cạnh đó, các GVTTL cũng tích cực trong việc đưa các lập luận, giải thích cho câu trả lời của HS trong bài tập 3.3.
HS 1 đã nhầm lẫn biểu đồ histogram là biểu đồ cột nên dựa vào sự chênh lệch của các cột để suy ra độ phân tán của dữ liệu. | |
GVTTL D61: | Câu trả lời đúng là của HS 2. Ở đây HS 2 có thể sử dụng phương sai để giải thích hoặc so sánh độ phân tán dựa vào hình dạng phân bố của biểu đồ. |
GVTTL D40: | Lí do từ đâu HS 3 đã trả lời như vậy? |
GVTTL D65: | HS 3 cho rằng biểu đồ nào có nhiều cột giá trị dữ liệu nhất thì có độ phân tán cao nhất. |
Mặc dù đã có những trao đổi sâu sắc hơn về các phương án trả lời của HS nhưng khi thực hành dạy học lần một, GV D47 vẫn đang còn lúng túng trong việc đưa ra những bằng chứng kiến thức lập luận cho một số ý kiến HS đưa ra. Điều này được cải thiện tốt hơn trong tiết dạy thực hành lần hai sau khi các GVTTL cùng
phản ánh lại tiết dạy lần một. Việc phân tích rõ bản chất kiến thức trong câu trả lời của HS giúp cho các GVTTL có một cách nhìn khái quát, đẩy đủ hơn. Từ đó, SCK của các GVTTL được nâng cao nhằm phục vụ tốt cho việc dạy học. Điều này cũng được các GVTTL nhận thấy khi đưa ra nhận xét cuối chu trình.
Hình 5.15. Minh họa phản hồi của GVTTL D61 về SCK trong phiếu phỏng vấn
5.4.3. Sự tiến triển kiến thức về việc học của học sinh của giáo viên toán tương lai để dạy học độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram qua nghiên cứu bài học
a) Kiến thức về việc học của học sinh của giáo viên toán tương lai để dạy học độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram
Bài tập 2.4, 3.4 nhằm mục đích khám phá kiến thức của GV về những khó khăn tiềm ẩn của HS khi so sánh độ phân tán của dữ liệu thể hiện trên biểu đồ cột và biểu đồ histogram, cũng như những lí do đằng sau những phản ứng và khó khăn đó. Bằng cách tập trung vào các khía cạnh của KCS, câu hỏi này đánh giá sâu hơn kiến thức về việc học của HS (KCS).
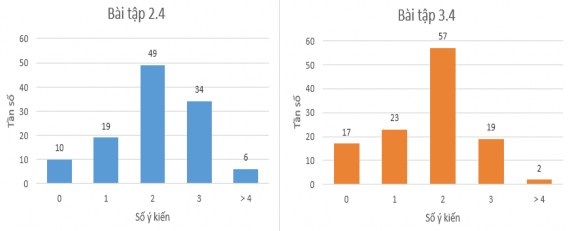
Hình 5.16. Biểu đồ số ý kiến của GVTTL về KCS trong thực nghiệm 3
Các ý kiến của GVTTL đưa ra được chúng tôi tập hợp và phân loại theo các cụm từ khóa liên quan đến kiểu kiến thức này. Mặc dù, chúng tôi phân loại thành 7 khó khăn, sai lầm hay gặp phải nhưng mỗi GVTTL chỉ nêu được nhiều nhất 4 ý kiến. Trong đó, tỉ lệ những GVTTL nêu được 4 ý kiến hợp lí rất thấp (6 GV ở bài tập 2.4 và 2 GV ở bài tập 3.4). Khoảng gần một nửa số GVTTL nêu được 2 khó khăn sai lầm của HS. Trong bài tập 2.4, các GVTTL đa số tập trung vào các sai lầm như “độ phân tán của dữ liệu được so sánh thông qua giá trị trung bình và cho rằng độ phân tán của dữ liệu là như nhau nếu chúng có giá trị trung bình bằng nhau” hay “độ phân tán của dữ liệu phụ thuộc vào chiều cao của cột giá trị, nếu chiều cao của cột giá trị càng lớn thì độ phân tán càng cao”. Bên cạnh đó, các sai lầm trong trường hợp độ phân tán của dữ liệu trên biểu đồ histogram (bài tập 3.4) được nêu ra chủ yếu là các ý tưởng “biểu đồ histogram nào có sự chênh lệch các cột nhiều nhất thì có độ phân tán cao nhất” hay “biểu đồ histogram nào có số lượng cột nhiều hơn thì có độ phân tán lớn hơn”. Một số khó khăn chung cũng được các GVTTL nêu ra như “không nắm được khái niệm độ phân tán của dữ liệu và không biết độ phân tán được đo bằng những tham số nào” hoặc “không xác định được loại biểu đồ và không biết cách đọc thông tin trên biểu đồ”. Về cơ bản, các GVTTL cũng nêu được một số khó khăn, sai lầm phổ biến của HS khi học độ phân tán của dữ liệu biểu diễn trên biểu đồ tuy nhiên vẫn chưa đầy đủ. Bên cạnh đó, rất ít GVTTL có thể giải thích nguyên nhân những sai lầm này của HS. Điều này cho thấy, các GVTTL chưa tích lũy đầy đủ kiến thức về những suy nghĩ, tư duy của HS để có thể tham gia vào quá trình dạy học nội dung này một cách hiệu quả.
Bảng 5.17. Minh họa câu trả lời cho KCS của GVTTL trong thực nghiệm 3
Ví dụ minh họa | |
H19 đưa ra 4 khó khăn sai lầm hợp lí cho bài tập 2.4 |
|
D11 đưa ra được 4 ý kiến hợp lí cho bài tập 3.4 |
|
D21 đưa ra 4 ý kiến nhưng chỉ đúng 3 ý kiến cho bài tập 3.4 |
|
H46 đưa ra 3 ý kiến nhưng chỉ đúng 2 ý kiến trong bài tập 3.4 |
|
b) Sự tiến triển kiến thức về việc học của học sinh của giáo viên toán tương lai để dạy học độ phân tán trên biểu đồ cột và biểu đồ histogram qua nghiên cứu bài học
KCS của GVTTL là khả năng dự đoán những khó khăn phổ biến của họ như khó khăn trong việc dùng tham số nào để mô tả độ phân tán của dữ liệu hay việc xác định, ước lượng giá trị trung bình trên biểu đồ cột và biểu đồ histogram. Một thành phần khác của kiểu kiến thức này là khả năng hiểu rõ cách thức HS tư duy hay những quan niệm sai lầm của HS khi học về độ phân tán của dữ liệu thể hiện trên biểu đồ cột và biểu đồ histogram, chẳng hạn như HS so sánh độ phân tán của dữ liệu bằng cách so sánh giá trị trung bình hay xét độ phân tán của dữ liệu bằng cách xét sự chênh lệch của các cột tần số trong biểu đồ histogram.
NCBH đã mang lại một môi trường tốt để các nhóm cùng thảo luận đưa ra những nhận xét chung về các thành phần kiến thức của KCS và nó được bộc lộ ra trong các bước chuẩn bị và thực hiện kế hoạch bài dạy của bài học nghiên cứu. Trong suốt quá trình thảo luận chỉnh sửa kế hoạch bài dạy, các GVTTL đã phải chỉnh sửa và bổ sung các câu hỏi dự đoán và các tình huống trả lời của HS có thể xảy ra. Điều này giúp các GVTTL trong quá trình thực hành giảng dạy đã thể hiện một cách tự tin, chủ động. Họ đã chỉ ra cho HS thấy những lỗi sai và giải thích cho HS hiểu đồng thời họ cũng đề ra những nhiệm vụ phù hợp nhằm đánh giá đúng khả năng, tạo động lực học tập và phát triển năng lực cho HS. Sau lần dạy thực hành thứ nhất, các GVTTL và nhà nghiên cứu đã đưa ra nhưng phản ánh giúp củng cố kiến thức về cách thức đặt câu hỏi hay giải đáp những thắc mắc nhằm làm rõ tư duy của HS.
Các bạn nhận thấy gì về sự hiểu biết nội dung độ phân tán của dữ liệu của HS thể hiện trên biểu đồ cột và biểu đồ histogram? | |
GVTTL D47: | Đối với nhiệm vụ so sánh độ phân tán lượng mưa hai vùng trên biểu đồ cột, một số HS nghĩ rằng phải tính giá trị phương sai của hai biểu đồ thì mới so sánh được nên khi biểu đồ cho không có các giá trị cụ thể HS nói rằng không so sánh được. Một số HS khác thì nhận xét theo cảm giác trực quan hình dạng của biểu đồ chứ không giải thích bằng bản chất toán học được. |
GVTTL D61: | Một điều đáng chú ý là khi HS đã biết cách xác định độ phân tán của dữ liệu dựa hình dạng của biểu đồ cột, HS lại áp dụng kiến thức đó vào biểu đồ histogram nên dẫn đến sai lầm. |
Nhà nghiên cứu: | Từ những khó khăn và sai lầm của HS, chúng ta cần phải phân tích rõ hơn những bản chất kiến thức giúp học sinh hiểu rõ hơn. |
Từ những phân tích trên, các GVTTL đã có những bước chỉnh sửa trong các lần soạn kế hoạch bài dạy tiếp theo. Bên cạnh đó, Những phản hồi tích cực về sự phát triển kiến thức KCS khi tham gia NCBH cũng được các GVTTL nêu ra trong phiếu phỏng vấn cuối thực nghiệm.
Hình 5.17. Phản hồi của GVTTL H34 vể KCS trong thực nghiệm 3
5.4.4. Sự tiến triển kiến thức về việc dạy của giáo viên toán tương lai để dạy học độ
phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram qua nghiên cứu bài học
a) Kiến thức về việc dạy của giáo viên toán tương lai để dạy học độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram
KCT có thể được đánh giá thông qua việc hiểu biết về các cách thức, phương pháp khác nhau để giảng dạy một ý tưởng toán học cụ thể, cũng như biết cách triển khai chúng hiệu quả. Bài tập 2.5 và 3.5 đặt ra để nhằm đưa ra bằng chứng về khả năng hiểu biết về việc dạy học độ phân tán của dữ liệu trên biểu đồ cột và biểu đồ histogram của các GVTTL. Việc cung cấp những chỉ dẫn, lưu ý cụ thể trong dạy học chứng tỏ người GV am hiểu nội dung về độ phân tán của dữ liệu, cách thức mô tả hay nhìn nhận chúng trên biểu đồ kết hợp với khả năng truyền đạt nội dung này một cách hiệu quả.
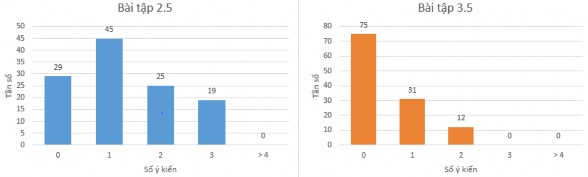
Hình 5.18. Biểu đồ số ý kiến của GVTTL về KCT trong thực nghiệm 3
Biểu đồ hình 5.17 tổng hợp số ý tưởng mà các GVTTL đưa ra. Ở bài tập 2.5, có đến 29 (24,58%) GVTTL không nêu được chỉ dẫn nào để hướng dẫn HS xác định độ phân tán của dữ liệu trên biểu đồ cột. Đa số các GV nêu được một đến hai chỉ dẫn cho HS chủ yếu tập trung vào các chỉ dẫn “trên biểu đồ cột ta so sánh giá trị của các cột với giá trị trung bình, nếu mức độ chênh lệch giá trị dữ liệu của biểu đồ nào lớn hơn thì sẽ có độ phân tán lớn hơn” hay “dựa vào hình dạng phân bố của biểu đồ cột, nếu biểu đồ có hình dạng bằng phẳng hơn thì sẽ có độ phân tán thấp hơn biểu đồ có hình dạng nhấp nhô”. Ở bài tập 3.5 với yêu cầu nêu các chỉ dẫn giúp HS xác định độ phân tán của dữ liệu trên biểu đồ histogram thì có đến 63,55% (75) GVTTL không đưa ra phản hồi nào. Các GVTTL còn lại chỉ nêu đúng được 1 đến 2 chỉ dẫn chủ yếu là “xác định hay ước lượng đường trung bình trên biểu đồ histogram, sau đó so sánh sự tập trung của dữ liệu gần xung quanh đường trung bình. Biểu đồ nào có nhiều dữ liệu gần đường trung bình hơn thì có độ phân tán nhỏ hơn”. Rất ít GVTTL đưa ra hướng dẫn cách xác định độ phân tán của dữ liệu dựa vào hình dạng của biểu đồ histogram.
Bảng 5.18. Minh họa câu trả lời cho KCT của GVTTL trong thực nghiệm 3
Ví dụ minh họa | |
H09 đưa ra được 3 chỉ dẫn cho bài tập 2.5 |
|
| |
H04 đưa ra nhiều chỉ dẫn nhưng chỉ đúng 2 chỉ dẫn |
|
D10 đưa ra nhiều chỉ dẫn nhưng chỉ đúng 2 chỉ dẫn |
|
