Hàm Khuếch Đại Biên Độ A Với  = Opt Và  = 0 Hệ Chính Có 3 Bậc Tự Do.

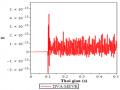
Với việc lắp DVA tối ưu vào hệ thống, tại tần số cộng hưởng = 0.88 dao động xoắn được bình ổn trong khoảng thời gian ngắn (khoảng 0.13s) với biên độ nhỏ dưới

0.012 rad (hình 4.24).

a) Không lắp DVA

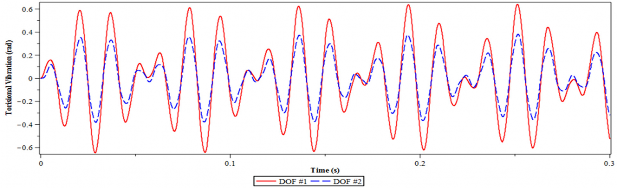
b) Có lắp DVA tối ưu

Hình 4.25. Dao động xoắn của hệ chính 2 bậc tự do tại tần số = 0.46

Hình 4.25 mô tả đáp ứng dao động xoắn của hệ thống có 2 bậc tự do có lắp bộ hấp thụ DVA tối ưu tại tần số cộng hưởng = 0.46. Bằng việc so sánh các đáp ứng trên hình 4.25a và 4.25b, rõ ràng rằng việc lắp DVA tối ưu mang lại hiệu quả tốt với cả hai bậc tự do so với trường hợp khi chưa lắp DVA tối ưu. Trong chế độ dao động bình ổn (0.15 trở đi), biên độ dao động của bậc tự do thứ nhất chỉ còn 0.12 rad, bậc tự do thứ hai chỉ còn 0.08 rad, trong khi biên độ dao động cực đại với trường hợp chưa lắp DVA tại tần số cộng hưởng = 0.46 là 1.2 rad. Với biên độ dao động rất lớn như vậy sẽ gây nguy hại cho trục, trục có thể bị phá hủy ngay lập tức do biến dạng xoắn quá lớn. Việc lắp DVA tối ưu trong trường hợp này mang lại hiệu quả kỹ thuật rất lớn và ý nghĩa.

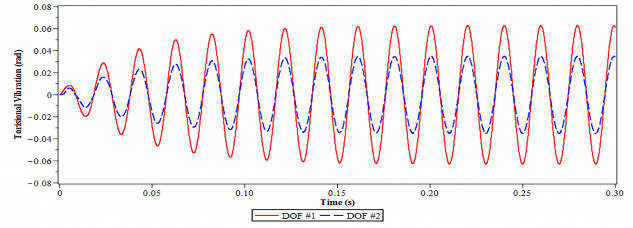
a) Không lắp DVA

b) Có lắp DVA tối ưu

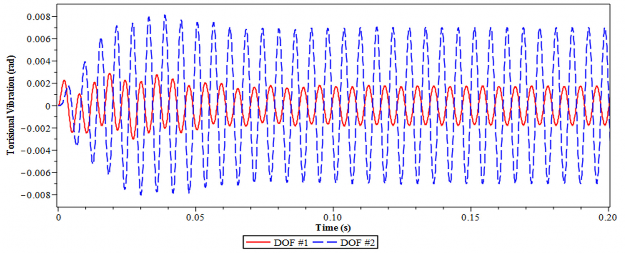
Hình 4.26. Dao động xoắn của hệ chính 2 bậc tự do tại tần số = 1.58

Hiệu quả giảm dao động xoắn của thiết kế DVA theo nghiệm giải tích tối ưu tìm được ở trên còn được thể hiện tại tần số cộng hưởng = 1.58.

Hiệu quả này được thể hiện rõ ràng khi so sánh đáp ứng dao động trong hình 4.26a và 4.26b. Từ hình 4.26a ta thấy rằng dao động xoắn của hệ với cả hai bậc tự do trong trường hợp không lắp DVA là không ổn định.

Trong khi với trường hợp có lắp DVA tối ưu, thứ nhất dao động xoắn có hại nhanh chóng được bình ổn trong khoảng thời gian 0.8s trở đi, thứ hai biên độ dao động là nhỏ: khoảng 0.04rad với bậc tự do thứ hai và 0.004 rad với bậc tự do thứ nhất.

Mô phỏng số trường hợp hệ chính có 3 bậc tự do

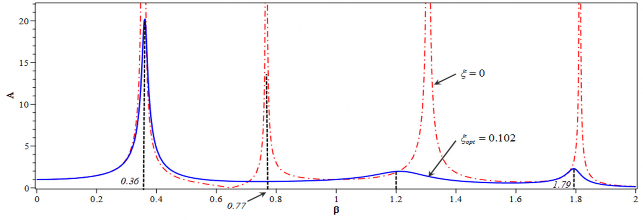
Hình 4.27. Hàm khuếch đại biên độ A với = opt và = 0 hệ chính có 3 bậc tự do.

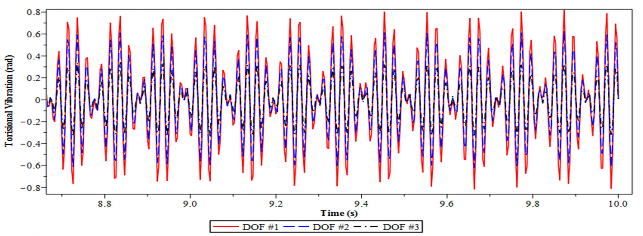
a) Không lắp DVA

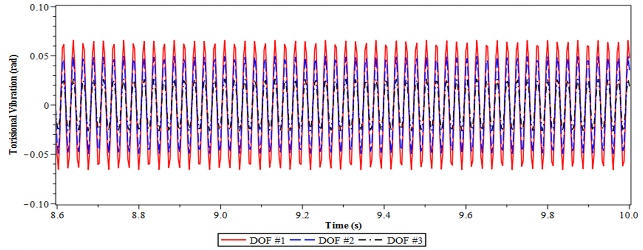
b) Có lắp DVA tối ưu

Hình 4.28. Dao động xoắn của hệ chính 3 bậc tự do tại tần số = 0.36

Hình 4.27 mô tả sự thay đổi của hàm khuếch đại biên độ A với trường hợp hệ chính có 3 bậc tự do. Từ hình 4.27 ta thấy vùng cộng hưởng được xác định tại = 0.36, 0.77, 1.2, và 1.76.

Trong trường hợp này, ngoại trừ vùng cộng hưởng đầu tiên ở = 0.36, sự dao động ở các điểm cộng hưởng khác (= 0.77, 1.2, và 1.76.) bị triệt tiêu một cách hiệu quả với giá trị tương đối nhỏ của A.

Hình 4.28 và 4.29 minh họa dao động của hệ thống 3 bậc tự do có lắp và không lắp DVA tối ưu tại tần số cộng hưởng = 0.36 và 0.77.

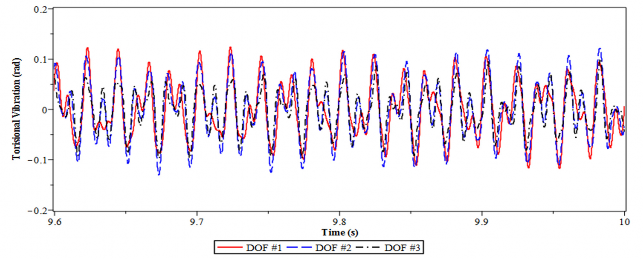
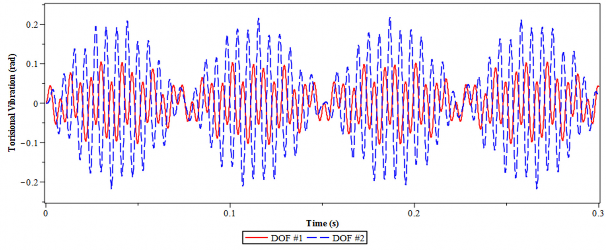
a) Không lắp DVA

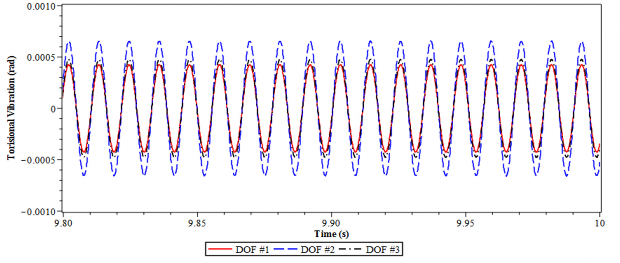
b) Có lắp DVA tối ưu

Hình 4.29. Dao động xoắn của hệ chính 3 bậc tự do tại tần số = 0.77

126

Từ hình 4. 28 và 4.29, một lần nữa ta lại thấy rằng trong trường hợp có DVA tối ưu làm giảm đáng kể biên độ dao động của hệ thống so với trường hợp khi chưa lắp DVA. Hiệu quả giảm dao động của DVA tối ưu trong trường hợp này không những được thể hiện qua việc bình ổn dao động xoắn có hại trong thời gian ngắn mà còn thể hiện biên độ giao động giảm rõ rệt và có giá trị nhỏ. Trong khi đó khi chưa lắp DVA tối ưu, dao động xoắn không ổn định, có biên độ cực đại là lớn, khoảng 1.6 rad (bậc tự do thứ nhất) tại tần số cộng hưởng = 0.36.

4.3. Kết luận chương 4.

Chương 4 luận án, tác giả đã nghiên cứu các vấn đề sau:

- Tác giả đã nghiên cứu, phân tích, đánh giá hiệu quả giảm dao động xoắn cho trục máy trong trường hợp không lắp bộ hấp thụ dao động và trường hợp có lắp bộ hấp thụ dao động với các nghiệm giải tích tối ưu tìm được của bộ hấp thụ dao động DVA theo bốn phương pháp như sau:

Mô men kích động

Thiết kế DVA	Hiệu quả giảm dao động (%)
	cs = 0 kgm2/s	cs = 5 kgm2/s	cs = 22.5 kgm2/s
Kích động tuần hoàn	(DVA-FPM)	99.987	94.939	68.178
Kích động va chạm	(DVA-MKE)	99.473	95.46	81.674
Kích động ngẫu nhiên	(DVA-MQT)	97.058	95.464	95.758
	(DVA-MEVR)	96.988	95.909	96.013

Có thể bạn quan tâm!

• Năng Lượng E Với Dva-Mevr Khi Hệ Chính Không Cản Chịu Kích Động Ngẫu Nhiên
• Sự Thay Đổi Của Đường Cong Khuếch Đại Biên Độ Khi Thay Đổi Tỷ Số Cản Với
• Tham Số Tối Ưu Ξ Theo Số Bậc Tự Do Của Hệ Chính
• Nghiên cứu giảm dao động xoắn của trục máy bằng bộ hấp thụ dao động - 18
• Nghiên cứu giảm dao động xoắn của trục máy bằng bộ hấp thụ dao động - 19

Xem toàn bộ 153 trang tài liệu này.

Kết quả này khẳng định các tham số tối ưu của bộ DVA tìm được trong luận án có hiệu quả giảm dao động tốt trong cả trường hợp hệ chính có cản và không cản.

- Đã áp dụng các kết quả nghiên cứu, tính toán các thông số tối ưu của bộ hấp thụ động DVA và mô phỏng số các kết quả nghiên cứu. Từ việc mô phỏng số các kết quả nghiên cứu trong trường hợp hệ chịu kích động điều hòa, kích động va chạm và kích

động ngẫu nhiên ta thấy rằng hiệu quả giảm dao động của các thiết kế DVA là rất tốt. Với trường hợp hệ chịu kích động điều hòa, ngay cả khi hệ làm việc trong vùng cộng hưởng thì hiệu quả giảm dao động khi hệ chính không cản và có cản đều rất tốt. Điều này đáp ứng được yêu cầu của kỹ thuật đặt ra.

- Đã phát triển các kết quả nghiên cứu cho trường hợp hệ chính có nhiều bậc tự do. Tác giả đã thiết lập được hệ phương trình vi phân mô tả dao động của hệ và tìm được tham số tối ưu của bộ DVA giảm dao động cho hệ nhiều bậc tự do theo phương pháp hai điểm cố định.

KẾT LUẬN VÀ KIẾN NGHỊ

Các kết quả chính của luận án:

Luận án tập trung nghiên cứu tính toán xác định các tham số tối ưu của bộ hấp thụ dao động DVA giảm dao động xoắn cho mô hình trục máy có 1 và nhiều bậc tự do. Các tham số tối ưu của bộ hấp thụ dao động DVA gồm tỷ số α (tỷ số giữa tần số riêng của bộ hấp thụ dao động DVA và tần số riêng của hệ chính) và tỷ số cản nhớt ξ.

1. Tác giả đã thiết lập mô hình cơ học và mô hình toán học để xác định dao động xoắn của trục có sử dụng bộ hấp thụ dao động DVA. Để tìm phương trình vi phân dao động của cơ hệ, tác giả sử dụng phương trình Lagrange loại II. Hệ phương trình vi phân thu được là hệ tuyến tính. Từ hệ phương trình vi phân mô tả dao động xoắn của trục, nhận thấy có chứa các đại lượng của bộ hấp thụ dao động, đây chính là cơ sở để các nhà khoa học nghiên cứu, phân tích, tính toán tìm các thông số của bộ hấp thụ dao động theo các tiêu chuẩn tối ưu khác nhau.

2. Tác giả đã nghiên cứu xác định được tham số tối ưu của bộ DVA dưới dạng biểu thức giải tích tường minh, giảm dao động xoắn cho trục máy có 1 bậc tự do chịu tác dụng của các kích động khác nhau.

Trường hợp trục máy chịu kích động điều hòa:

2

2

3

2n(1 2)



n

opt 

2  1;

opt

Trường hợp trục máy chịu kích động ngẫu nhiên:

- Nghiệm giải tích tối ưu theo phương pháp cực tiểu mô men bậc hai:

2

n(2 2 )

opt 2

;

n(1 2 )

opt 

2 2(4  32 )

22 n(1 2 )(2 2 )

2

2



n

- Nghiệm giải tích tối ưu theo phương pháp cực đại độ cản tương đương:

opt

;

n(1 2)



opt 

Trường hợp trục máy chịu kích động va chạm:

opt 

2n(2 2 )

;

2n(1 2 )

opt 

2 (4  32 24 )

(1 2 )2 2n(2 2 )

3. Tác giả đã nghiên cứu, phân tích, đánh giá hiệu quả giảm dao động xoắn cho trục máy trong trường hợp không lắp bộ hấp thụ dao động và trường hợp có lắp bộ hấp thụ dao động với các nghiệm giải tích tối ưu tìm được của bộ hấp thụ dao động DVA. Từ việc mô phỏng số biên độ dao động theo thời gian trong trường hợp hệ chịu kích động điều hòa, kích động va chạm và kích động ngẫu nhiên ta thấy rằng biên độ giảm dao động của trục máy khi thiết kế DVA theo các tham số tối ưu tìm trong luận án là rất tốt. Với trường hợp hệ chịu kích động điều hòa, ngay cả khi hệ làm việc trong vùng cộng hưởng thì hiệu quả giảm dao động đều rất tốt. Điều này đáp ứng được yêu cầu của kỹ thuật đặt ra.

4. Đã phát triển các kết quả nghiên cứu cho trường hợp hệ chính có nhiều bậc tự do. Tác giả đã thiết lập được hệ phương trình vi phân mô tả dao động của hệ, thiết lập được biểu thức tổng quát của hàm khuếch đại biên độ của bậc tự do thứ N trong mô hình trục máy có N bậc tự do và tìm được tham số tối ưu của bộ DVA giảm dao động xoắn cho hệ nhiều bậc tự do dưới dạng giải tích.

2n 2132 2

- Tham số tối ưu của bộ DVA với mô hình trục máy có 2 bậc tự do:

opt 

2n 212

1 (436  624  52  2)(224  52  2)22

2

n4(2  32)(12)3

opt 

- Tham số tối ưu của bộ DVA với mô hình trục máy có 3 bậc tự do:

Xem tất cả 153 trang.