Tham Số Tối Ưu Ξ Theo Số Bậc Tự Do Của Hệ Chính

Xác định tỷ số ξ tối ưu

Để xác định ξ tối ưu ta giải phương trình Từ phương trình (4.57) ta có:

A 0



N 2 1

N 1 3

N 2 2

A2A A A A 22A A

A A 2A2A22

(4.68)

N 1 4 1 2

Đạo hàm hai vế của phương trình (4.68) theo β ta thu được

2 A A A

A A 22A A

A A 2A

N 2 1

N 1 3

N 2 2

N 1 4 

 2( A A

A A )( AN 2

A A

A1 AN 1 A A

A3 ) 

N 2 1

N 1 3 1

N 2 

3

N 1 

A2 

2( A A

A A )( AN 2 A A A2 AN 1 A A

A4 )2 

N 2 2

N 1 4 2 N 2 

4

N 1 



 2 A A1  2 A

A2 2

1 

Chú ý điều kiện

A 0



2 

(4.69)

(4.70)

Giải hệ phương trình (4.69), (4.70) ta thu được:

2 AN1 

AN2 

2 2 

A1 2

A3

A A3 

A1

AN2A1 AN1A3AA3AN1AN2 A1AN2A1A AN1AN2A1 AN1A3

2 

2 AN2 

AN1 

2 2

A2 2

A4

A A2 

A4 

AN2A2 AN1A4AA2AN2 A4AN1AN2A2A AN1AN2A2 AN1A4



2 AN1 

AN2 

2 2

A1

A1 2

A3

A A3

A1

A1AN2 A3AN1A A3AN1AN2 A1AN2A1 A AN1A1AN2 A3AN1

2 

2 AN2 

AN1 

2 2

A2

A2 2

A4

A A2

A4 

A2AN2 A4AN1A A2AN2 A4AN1AN2A2 A AN1A2AN2 A4AN1



2 AN1 

AN2 

2A1 2

A3

A1

A A3 

A1

A1AN2 A3AN1AN2AA3AN1 A1AN2AN1AA1AN2 A3AN1A1 

2 

2 AN2 

AN1 

2 A2 2

A4

A2

A A2 

A4 

A2AN2 A4AN1AN2AA2AN2 A4AN1AN1AA2AN2 A4AN1A2 



2 AN 1

AN 2 

2 A3

A1 

A1

A A3 

A1 

A1AN 2 A3AN 1 A A1AN 2 A3AN 1AN 1 AN 2 A1 

2 



2 AN 2 

AN 1 

2 

A2

A4 

A2

A A2 

A4 

A2AN2 A4AN1A

A2 AN 2 A4 AN 1AN 2 AN 1 A2 



Cuối cùng ta thu được biểu thức tối giản của tỷ số cản như sau:

A2 A A A A

A AN 1 A AN 2 A

A3 A A1 A A1

1 N 2 3

N 1 3 

1 

N 1 N 2 

1 

2 



A2 A A

A A

A

AN 2 A

AN 1 A

A2 A

A4 A

A2

2 N 2 4

N 12 

4 

N 2 

N 1 

2 



Thay các giá trị tối ưu α = αopt và β1 =β1,opt vào phương trình (4.71) ta thu được:

(4.71)

2 

A2A A

1 N2

A A

3 N1 3









A

1



A



N









A

A

A 

A

N1 

3 A

N2 



A

1 

A2 A A

2 N2 4 N12

A A







A



A 





A

4 N2 N1 





A

A2 A A4 A A2



2 

opt,1,opt

(4.72)

Thay các giá trị tối ưu α = αopt và β2 =β2,opt vào phương trình (4.71) ta thu được:

A2AA

1 N2 3 N1 3

A A







A



A





A

A 

A





A

1 N1 N2 



A

3 A



A

1 

A2 A A

2 N2

A A

4 N12







A



A









A





N2 

A2 A A4 A A2

N1 



2 

2 

Theo Brock [14] tỷ số cản tối ưu ξopt được xác định theo công thức:

opt,2,opt

(4.73)

opt

* 

(4.74)

22

Thay (4.72), (4.73) vào phương trình (4.74) ta thu được tỷ số cản tối ưu. Các kết quả giải tích của tỷ số cản nhớt ξ thu được được liệt kê trong bảng 4.8.

Bảng 4.8. Tham số tối ưu ξ theo số bậc tự do của hệ chính

Số bậc tự do

Biểu thức giải tích tối ưu của ξ
N=1	2 3 2 2n(12)
N=2	1 AB 2 C A  (436  624  52  2) B  (224  52  2)22;C n4(2  32)(12)3
	2 ABC
	2 DE
N=3…	A 22; B  248  736  624  22  2
	C  5361424102 2; D n4124
	E  248 1336  2624 182  4

Có thể bạn quan tâm!

Xem toàn bộ 153 trang tài liệu này.

4.2.3. Tính toán mô phỏng số các kết quả nghiên cứu cho hệ chính nhiều bậc tự do

Hình 4.20 mô tả sự thay đổi đường cong khuếch đại biên độ theo tỷ số cản nhớt. Hình 4.20 chỉ ra rằng có một số vùng cộng hưởng, chẳng hạn tại các tần số = 0.392, 0.873 và 1.648. Rõ ràng rằng với giá trị của tỷ số cản nhớt tối ưu ξopt=0.23 tại các đỉnh cộng hưởng đường cong khuếch đại biên độ có độ cao thấp nhất so với các đường cong A khác ứng với các giá trị khác nhau của ξ.

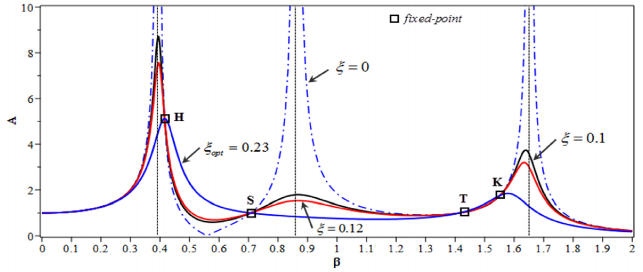
Hình 4.20. Hàm khuếch đại biên độ-tần số với các giá trị khác nhau của tỷ số cản nhớt với N=2, µ = 0.02, η = 1, γ = 0.5, λ= 0.8, n = 6 and α = αopt = 0.708.

Bảng 4.9 trình bày các giá trị của hàm A ở các vùng cộng hưởng của các đường cong trong hình 4.20. Từ bảng 4.9, nhận thấy rằng không chỉ giá trị của A tại vùng cộng hưởng được kiểm soát của đường cong được tối ưu mà còn cả các giá trị tại các vùng cộng hưởng khác sẽ được giảm xuống khi so sánh đến các đường cong mà không có tối ưu ξ.

Bảng 4.9. Giá trị hàm khuếch đại A tại các tần số cộng hưởng của hệ khi thay đổi tỷ số cản nhớt .

Tỷ số cản nhớt

Hàm khuếch đại biên độ A
= 0.392	= 0.873	= 1.648
ξ = 0.1	8.772	1.885	3.734
ξ = 0.12	7.655	1.503	3.116
ξopt= 0.23	4.463	0.992	1.263

Để mô phỏng số các kết quả nghiên cứu ở trên, tính toán sẽ được thực hiện với các số liệu mô phỏng trong bảng 4.10. Trục máy được kích thích bởi một mô men xoắn với biên độ 5 Nm và tần số kích thích khác nhau. Các đại lượng không thứ nguyên được tính toán và thể hiện trong bảng 4.11. Bảng 4.12 cho thấy các kết quả tối ưu được tính theo các tham số đầu vào đã xác định.

Bảng 4.10. Các thông số mô phỏng cho trường hợp hệ chính nhiều bậc tự do.

Tham số

Đơn vị	Giá trị	Tham số	Đơn vị	Giá trị
mr	[kg]	5.0	e2	[m]	0.09
ma	[kg]	0.2	Jr	[kgm2]	2E-02
r	[m]	0.1	Ja	[kgm2]	2E-03
a	[m]	0.1	ks	[Nm/rad]	1E+04
e1	[m]	0.06	N	-	6

Bảng 4.11. Giá trị của các đại lượng không thứ nguyên

Tham số

μ	η	γ	λ
Giá trị	0.04	1.0	0.6	0.9

Bảng 4.12. Giá trị các tham số tối ưu α và ξ theo số bậc tự do của hệ chính.

Số bậc tự do

Tần số β tại các điểm cố định

αopt

ξopt

N = 1

β1= 0.843;

β2= 1.052

0.619

0.112

N = 2

β1= 0.388;

β2= 0.707;

β3= 1.414;

β4= 1.557

0.632

0.220

N = 3

β1= 0.290; β2= 0.468;

β3= 1.001; β4= 1.190;

β5= 0.732; β6= 1.775

0.895

0.186

Mô phỏng số trường hợp hệ chính có 2 bậc tự do

Dao động xoắn của hệ chính 2 trong trường hợp không lắp và có lắp DVA tối ưu được thể hiện trên hình 4.21. Trong trường hợp này tần số mô phỏng được chọn là

= 0.04. Rõ ràng là các biên độ dao động trong trạng thái ổn định của hệ thống có lắp DVA đã được giảm đáng kể. Khi chưa lắp DVA tối ưu biên độ dao động xoắn của bậc tự do thứ nhất (DOF #1) và bậc tự do thứ hai (DOF #2) lần lượt là 0.4 rad và 0.6 rad. Trong khi đó với hệ thống có lắp DVA tối ưu, biên độ dao động trong 1s đầu tiên được giảm đi rõ rệt. Trong giai đoạn bình ổn (khoảng từ 1s trở đi) biên độ dao động xoắn chỉ còn là 0.002 rad đối với bậc tự do thứ nhất và 0.001 rad đối với bậc tự do thứ hai.

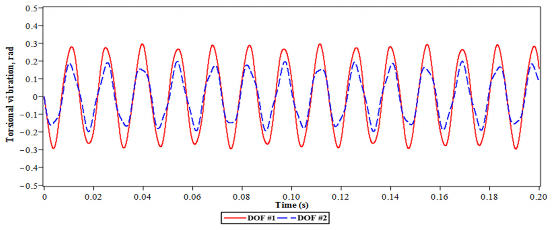
a) Không lắp DVA

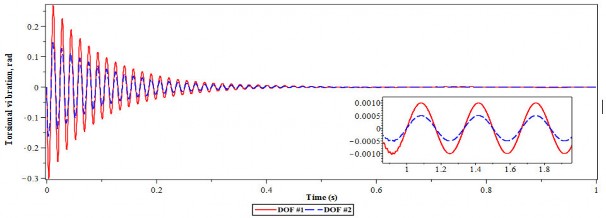
b) Có lắp DVA tối ưu

Hình 4.21. Dao động xoắn của hệ chính 2 bậc tự do tại tần số = 0.04

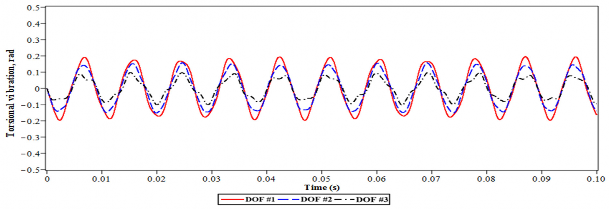
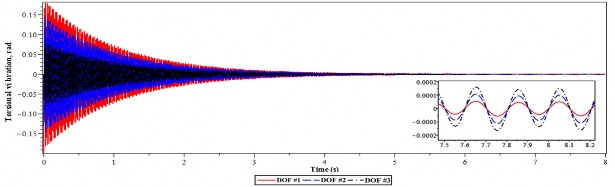
Tương tự, với trường hợp hệ chính có 3 bậc tự do, hiệu quả giảm dao động của DVA tối ưu được thể hiện trên hình 4.22. Hiệu quả giảm dao động của thiết kế DVA tối ưu là

tốt. Trong giai đoạn bình ổn biên độ dao động của cả ba bậc tự do đều nhỏ, khoảng dưới 0.0004 rad. Do đó, các công thức đề xuất đã được chứng minh ở trên là có hiệu quả để giảm dao động của cả hai hệ thống SDOF và MDOF.

a) Không lắp DVA

b) Có lắp DVA tối ưu

Hình 4.22. Dao động xoắn của hệ chính 3 bậc tự do tại tần số = 0.04

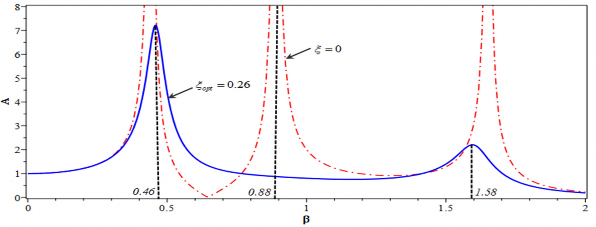
Hình 4.23. Hàm khuếch đại biên độ với = opt và = 0 với trường hợp hệ chính có 2 bậc tự do

121

Để chứng minh hiệu quả của thiết kế DVA tối ưu, các tính toán và mô phỏng số tiếp theo sẽ được thực hiện cho các hệ thống MDOF trong điều kiện cộng hưởng. Hình

4.23 mô tả sự thay đổi của hàm khuếch đại A trong trường hợp hệ chính có 2 bậc tự do với = opt và = 0. Từ hình 4.23 ta dễ dàng xác định được các vùng cộng hưởng của cơ hệ. Trên hình 4.23, tần số cộng hưởng tại = 0.46 và 1.58 có thể thấy rõ ràng. Sự rung động ở một điểm cộng hưởng khác tương ứng với tỉ lệ tần số điều khiển β = 0.88 bị triệt tiêu và gần như phẳng. Hình 4.24, 4.25 và 4.26 thể hiện đáp ứng dao động của hệ thống có 2 bậc tự do với thiết kế DVA tối ưu được tính toán tại các tần số nói trên. Rõ ràng là biên độ dao động của các hệ thống với DVA tối ưu thấp hơn đáng kể so với các hệ thống không có DVA.

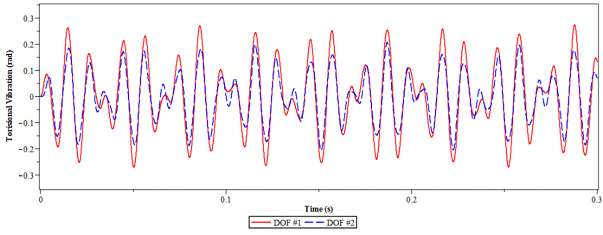
a) Không lắp DVA

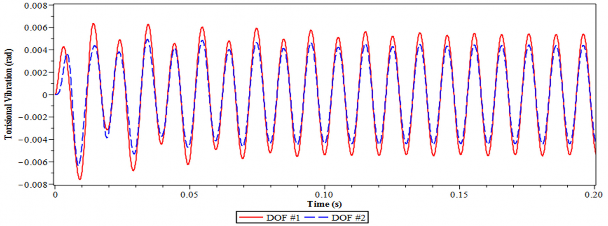
b) Có lắp DVA tối ưu

Hình 4.24. Dao động xoắn của hệ chính 2 bậc tự do tại tần số = 0.88