Năm 2016 Y. Wang và cộng sự nghiên cứu về điều khiển phản hồi nhiều đầu ra thích nghi dạng trượt cho AUV [116]. M.S.M. Aras và cộng sự (2016) đã đề cập đến điều khiển bằng Logic mờ cho độ sâu của ROV, dạng robot ngầm điều khiển qua dây cáp [66]. Z. Chu và D. Zhu (2016) nghiên cứu về điều khiển tối ưu dạng trượt cho AUV có tính đến tính năng động học của các thiết bị đẩy [80]. Trong [115] R. Cui và cộng sự đề xuất điều khiển thích nghi dạng trượt cho AUV với các đầu vào phi tuyến (2016).
Năm 2017 L. Shahaji nghiên cứu về điều khiển AUV [28], trong đó trình bày điều khiển bền vững cho nhiệm vụ dẫn đường của AUV. P. Londhe (2017) trình bày về điều khiển AUV và hệ thống tay máy dùng Logic mờ [29]. U. Ansari và A.H. Bajodah (2017) công bố nghiên cứu về điều khiển bền vững động học nghịch đảo cho AUV [65]. Cũng năm này M. Farhan và cộng sự (2017) đề xuất điều khiển MIMO kiểu trượt cho AUV [68]. B.N. Rath và cộng sự (2017) nghiên cứu về điều khiển hướng đi và độ sâu AUV với kỹ thuật điều khiển phản hồi mới [75]. C. Shen (2017) trình bày về thuật toán C/GMRES cho điều khiển dùng mô hình dự đoán phi tuyến đối với AUV [122].
Năm 2018 M.R. Ramezani-al và Z.T Sereshki trình bày nghiên cứu về bộ điều khiển thích nghi dạng trượt với luật thích nghi mới cho điều khiển bám quỹ đạo của AUV [74]. F. Yao và cộng sự (2018) trình bày các thí nghiệm đánh giá điều khiển độ sâu AUV dùng thuật toán điều khiển dự đoán nâng cao [78].
Các nghiên cứu được đề cập đến trong giai đoạn trên giúp gợi mở hướng nghiên cứu điều khiển AUV, các mô hình toán học có thể kế thừa cũng như các phương án điều khiển AUV thực thi các nhiệm vụ dưới nước. Các tài liệu trên trình bày nhiều cấu trúc AUV khác nhau, các phương pháp tổng hợp hệ thống điều khiển, giao tiếp điều khiển từ xa và các ứng dụng AUV trong thực tiễn khảo sát, nghiên cứu, tìm kiếm cứu nạn, …
1.2.2 Các nghiên cứu về điều khiển AUV tại Việt Nam
Tại Việt Nam việc nghiên cứu thuật toán điều khiển AUV đã xuất hiện nhưng cụ thể nghiên cứu thuật toán điều khiển thích nghi cho AUV với mạng nơ-ron thì còn ít gặp [3], [8], [9], các tài liệu cho thấy các nghiên cứu mới chỉ dừng lại ở việc thiết kế mô hình động lực cho các AUV với các thử nghiệm trong hồ thử ở độ sâu hạn chế. Tài liệu [7] của tác giả Nguyễn Đông trình bày khá chi tiết thiết kế và đánh giá động lực học của mô hình AUV. Tác giả cũng đề xuất thuật toán điều khiển hướng đi AUV trong mặt phẳng ngang và kiểm tra bằng thực nghiệm. Tuy nhiên nghiên cứu này chưa đề cập đến hoạt động của AUV ngầm dưới nước do hạn chế về cảm biến, hệ động lực và các yêu cầu kỹ thuật khác. Tác giả cũng nêu rõ giới hạn này trong tài liệu nghiên cứu của mình.
Các tổng kết trong [10] cũng chưa nói đến điều khiển AUV sử dụng thuật toán mạng nơ-ron nhân tạo thích nghi trong nghiên cứu hệ thống điều khiển. Tuy nhiên nghiên cứu chế tạo AUV này đã hoàn chỉnh về kết cấu và có thử nghiệm bước đầu, cơ sở nghiên cứu cũng tại TP Hồ Chí Minh. NCS hy vọng sẽ được hợp tác thử nghiệm các thuật toán điều khiển của mình khi có điều kiện. Nghiên cứu sinh nhận thấy việc kết hợp các kết quả nghiên cứu và phát triển thuật toán điều khiển thích nghi với các AUV là hướng đi rõ ràng.
Như vậy, vấn đề nghiên cứu của trong luận án mang tính thời sự và không trùng lặp với các công trình trước đó.
Có thể bạn quan tâm!
-
 Tổng Quan Về Robot Lặn Tự Hành Auv (Autonomous Underwater Vehicle)
Tổng Quan Về Robot Lặn Tự Hành Auv (Autonomous Underwater Vehicle) -
![Nghiên Cứu Auv Mô Hình Tại Trường Đh Bách Khoa Hà Nội [7]](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%2075%2075%22%3E%3C/svg%3E) Nghiên Cứu Auv Mô Hình Tại Trường Đh Bách Khoa Hà Nội [7]
Nghiên Cứu Auv Mô Hình Tại Trường Đh Bách Khoa Hà Nội [7] -
 Các Nghiên Cứu Về Điều Khiển Auv Trên Thế Giới
Các Nghiên Cứu Về Điều Khiển Auv Trên Thế Giới -
 Điều Khiển Tự Động Dùng Mạng Nơ-Ron Nhân Tạo
Điều Khiển Tự Động Dùng Mạng Nơ-Ron Nhân Tạo -
 Wij O J I , (3.29)
Wij O J I , (3.29) -
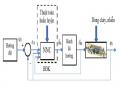
 Mô Hình Tổng Quát Của Bộ Điều Khiển Nnc Huấn Luyện Trực Tuyến
Mô Hình Tổng Quát Của Bộ Điều Khiển Nnc Huấn Luyện Trực Tuyến
Xem toàn bộ 169 trang tài liệu này.
Qua phân tích và đánh giá tình hình nghiên cứu ở trên, ta thấy điều khiển nơ-ron có tiềm năng rất lớn đối với các ứng dụng hàng hải nói chung và điều khiển AUV nói riêng. Việc nghiên cứu ứng dụng lựa chọn thuật toán thích nghi để nâng cao chất lượng bộ điều khiển dựa trên lý thuyết mạng nơ- ron nhân tạo cho hệ thống điều khiển phương tiện thủy luôn là vấn đề thời sự và cần phát triển hiện nay.
1.3 Kết luận chương 1
Trong chương 1 tác giả giới thiệu tổng quan về robot lặn tự hành AUV, các ứng dụng của AUV trên thế giới và tại Việt Nam trong thời điểm hiện nay. Mô hình toán học tổng quát của AUV trong không gian 3 chiều, 6 bậc tự do cũng được trình bày. Tác giả cũng tổng kết tình hình nghiên cứu về AUV và điều khiển AUV tiêu biểu trong khoảng 30 năm trở lại đây, nhằm làm nền tảng cho nghiên cứu, đánh giá ứng dụng của mình trong luận án.
CHƯƠNG 2
CƠ SỞ LÝ THUYẾT ĐIỀU KHIỂN NƠ-RON THÍCH NGHI THIẾT BỊ LẶN TỰ HÀNH
2.1 Mạng nơ-ron nhân tạo
Mạng nơ-ron nhân tạo (ANN) là một mô phỏng xử lý thông tin, được nghiên cứu từ hệ thống thần kinh của sinh vật, giống như bộ não để xử lý thông tin, bao gồm số lượng lớn các mối gắn kết cấp cao để xử lý các yếu tố làm việc trong mối liên hệ giải quyết vấn đề rõ ràng. ANN giống như con người, được học bởi kinh nghiệm, lưu những kinh nghiệm hiểu biết và sử dụng trong những tình huống phù hợp.
Đầu tiên ANN được giới thiệu năm 1943 bởi nhà thần kinh học Warren Mc Culloch và nhà lô-gic học Walter Pits. Nhưng với những kỹ thuật trong thời gian này chưa cho phép họ nghiên cứu được nhiều. Từ những năm cuối thế kỷ 20, đặc biệt là những năm gần đây, mô phỏng ANN xuất hiện và phát triển ngày càng rộng rãi. Các nghiên cứu ứng dụng đã được thực hiện trong các ngành: điện, điện tử, kỹ thuật chế tạo, y học, quân sự, giao thông, kinh tế,…và mới nhất là các nghiên cứu ứng dụng trong lĩnh vực điều khiển các phương tiện thủy.
2.1.1 Tổng quan về mạng nơ-ron nhân tạo trong điều khiển
2.1.1.1 Cấu trúc của mạng nơ-ron
a) Đơn vị xử lý
Một đơn vị xử lý, cũng được gọi là một nơ-ron hay một nút (node), thực hiện một công việc rất đơn giản: Nhận tín hiệu vào từ các đơn vị phía trước hay một nguồn bên ngoài và sử dụng chúng để tính tín hiệu ra sẽ được lan truyền sang các đơn vị khác (hình 1.1).
Trong đó:
wji
xi - Các đầu vào (i = 1,... n);
- Các trọng số tương ứng với các đầu vào;
j a j z j
g x
- Độ lệch (bias);
- Đầu vào mạng (net-input);
- Đầu ra của nơ-ron;
- Hàm truyền (hay hàm kích hoạt).
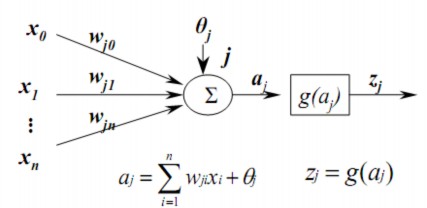
Hình 2.1 Đơn vị xử lý của mạng nơ-ron nhân tạo
Trong một mạng nơ-ron có ba kiểu đơn vị:
1) Các đơn vị đầu vào (Inputs units), nhận tín hiệu từ bên ngoài;
2) Các đơn vị đầu ra (Output units), gửi dữ liệu ra bên ngoài;
3) Các đơn vị lớp ẩn (Hidden units), tín hiệu vào (input) và ra (output) của nó nằm trong mạng.
Mỗi đơn vị j có thể có một hoặc nhiều đầu vào:
x0 , x1, x2 ,...xn , nhưng
chỉ có một đầu ra
z j . Mỗi đầu vào tới một đơn vị có thể là dữ liệu từ bên
ngoài mạng hoặc đầu ra của một đơn vị khác, hoặc là đầu ra của chính nó.
b) Hàm xử lý
- Hàm kết hợp: Mỗi đơn vị trong mạng kết hợp các giá trị đưa vào nó thông qua các liên kết với các đơn vị khác, sinh ra một giá trị gọi là đầu vào mạng (net input). Hàm thực hiện nhiệm vụ này gọi là hàm kết hợp, được định nghĩa bởi một luật lan truyền cụ thể. Trong phần lớn các mạng nơ-ron, thường giả sử rằng, mỗi một đơn vị cung cấp một bộ cộng như là đầu vào cho đơn vị mà nó có liên kết. Tổng đầu vào đơn vị j đơn giản là tổng trọng số của các đầu ra riêng lẻ từ các đơn vị kết nối cộng thêm ngưỡng hay độ lệch (bias) j
n
a jwjixij
i1
(2.1)
Một số trường hợp có thể sử dụng các thuật toán lan truyền phức tạp hơn, trong số đó là luật sigma-pi, có dạng:
n m
aj wji xik j
(2.2)
i1 k 1
Rất nhiều hàm kết hợp sử dụng một độ lệch hay ngưỡng để tính đầu vào mạng tới đơn vị. Đối với một đơn vị đầu ra tuyến tính, thông thường j được chọn là hằng số và trong bài toán xấp xỉ đa thức thì j 1.
- Hàm kích hoạt (hàm truyền): Phần lớn các đơn vị trong mạng nơ-ron chuyển đầu vào mạng bằng cách sử dụng một hàm vô hướng (scalar-to-scalar function) gọi là hàm kích hoạt, kết quả của hàm này là một giá trị gọi là mức độ kích hoạt của đơn vị. Loại trừ khả năng đơn vị đó thuộc lớp ra, giá trị kích hoạt được đưa vào một hay nhiều đơn vị khác. Các hàm kích hoạt hay được sử dụng hiện nay là:
Hàm truyền tuyến tính (Linear transfer function) (hình 2.2), được gọi
là hàm đồng nhất (Identity function).
g xx
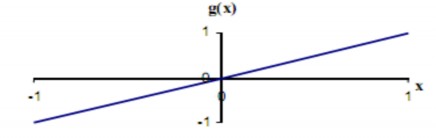
Hình 2.2 Hàm truyền tuyến tính
(2.3)
Hàm truyền giới hạn cứng (Hard - Limit transfer function), được biết đến với tên hàm ngưỡng (Threshold function hay Heaviside function) hay hàm bước nhị phân. Đầu ra hàm này được giới hạn vào một trong hai giá trị:
1, nếu x ≥ 0
g(x) = (2.4)
0, nếu x < 0
Dạng hàm này được sử dụng trong các mạng chỉ có một lớp. Trong hình 2.3, được chọn bằng 1.
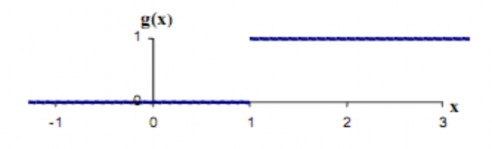
Hình 2.3 Hàm truyền giới hạn cứng
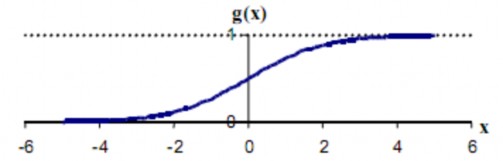
Hàm truyền dạng Sigma (Sigmoid transfer function) (hình 2.4): Hàm này thuận lợi khi sử dụng cho các mạng được huấn luyện bởi thuật toán lan truyền ngược (Back-propagation), bởi vì nó dễ lấy đạo hàm, do đó có thể giảm đáng kể tính toán trong quá trình huấn luyện. Hàm này hay được dùng cho chương trình ứng dụng mà các đầu ra mong muốn rơi vào khoảng [0,1].
gx
1
1 ex
(2.5)
2.5):
Hình 2.4 Hàm truyền dạng sigma
Hàm truyền dạng tang-sigma (tan-sigmoid transfer function) (hình
x
g x1 e
1 ex
(2.6)
Hàm này có thuộc tính tương tự hàm Sigma, có khả năng làm việc tốt đối với các ứng dụng có đầu ra yêu cầu trong khoảng [-1, 1].
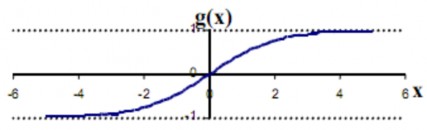
Hình 2.5 Hàm truyền dạng tang-sigma
Các hàm truyền của đơn vị ẩn (Hidden units) cần thiết cho việc biểu diễn sự phi tuyến vào trong mạng. Tuy nhiên, đối với luật học lan truyền ngược, hàm phải khả vi và sẽ có ích nếu như hàm được gắn trong một khoảng nào đó. Do vậy, hàm Sigma là lựa chọn thông dụng nhất.
2.1.1.2 Các hình trạng của mạng
Hình trạng của mạng được định nghĩa bởi: số lớp, số đơn vị trên mỗi lớp và sự liên kết giữa các lớp như thế nào. Các mạng về tổng thể được chia thành hai loại dựa trên cách thức liên kết các đơn vị:
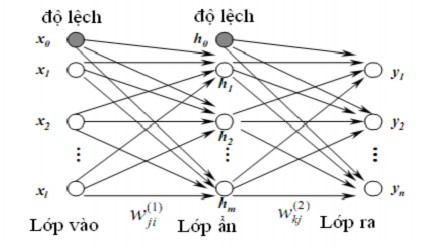
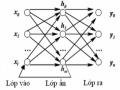
Hình 2.6 Mạng nơ-ron truyền thẳng nhiều lớp
- Mạng truyền thẳng (hình 2.6): Dòng dữ liệu từ đơn vị đầu vào đến đơn vị đầu ra được truyền thẳng. Việc xử lý dữ liệu có thể mở rộng ra nhiều lớp, nhưng không có các liên kết phản hồi. Nghĩa là, không thể có các liên kết mở rộng từ các đơn vị đầu ra tới các đơn vị đầu vào trong cùng một lớp hay các lớp trước đó.
- Mạng hồi quy (hình 2.7): Có chứa các liên kết ngược và khác với mạng truyền thẳng, các thuộc tính động của mạng mới quan trọng. Trong một


![Nghiên Cứu Auv Mô Hình Tại Trường Đh Bách Khoa Hà Nội [7]](https://tailieuthamkhao.com/uploads/2023/02/21/nghien-cuu-dieu-khien-thich-nghi-cho-robot-lan-tu-hanh-4-1-120x90.jpg)