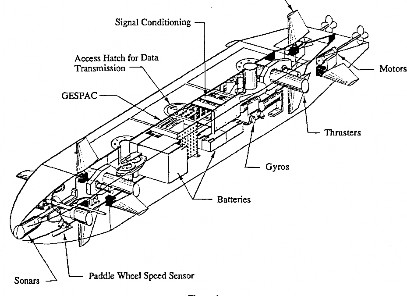
Hình 3.2 Sơ đồ cấu tạo các chi tiết của NSP AUV II
Mô hình AUV này có chiều dài 3m, rộng 0,4m và cao 0,25m. Vỏ bằng nhôm 6061 dày 0,25 inch. Trọng lượng toàn bộ là 220kg. Phần mũi làm bằng vật liệu mica đặc biệt chứa ắc-quy, các cảm biến, các mạch điện và công tắc. Nguồn cấp là ắc-quy 12V. Tốc độ cao nhất của AUV là 4 hải lý/giờ (knots), ở tốc độ này AUV duy trì thời gian làm việc được 4 giờ. AUV được thiết kế để hoạt động ở vùng nước nông với độ sâu hoạt động 30m, nếu gia cường thêm có thể hoạt động ở độ sâu tối đa 100m.
Cấu tạo hệ động lực AUV này gồm 2 cánh điều khiển hướng phía trước, 2 cánh điều khiển hướng phía sau; 2 cánh điều khiển độ sâu phía trước, 2 cánh điều khiển độ sâu phía sau; 2 chân vịt cố định phía sau vận hành bằng động cơ điện. Ngoài ra NSP AUV II còn có chân vịt đẩy theo chiều ngang (thruster) ở phía trước và phía sau, tuy nhiên với luận án này tác giả không sử dụng đến trong các mô phỏng điều khiển của mình.
3.1.2 Mô hình toán học AUV
Phần này mô tả sơ bộ phương pháp diễn giải phương trình động học tuyến tính 6 bậc tự do, các vấn đề chi tiết đã được trình bày trong [31]. Dạng tổng quát và đầy đủ của hệ phương trình động học được thể hiện trong (3.1) và (3.2).
ẋ = Ax + Bu (3.1)
[ẋ1
] = [
−M−1(C + D) −M−1g(t)
] [x1
] + [M−1
] τc (3.2)
ẋ2
JB/E(t) 0 20
x
Trong đó, x1(t) = Δν(t) = ν(t) - νref(t) và x2(t) = Δη(t) = η(t) - ηref(t) là các đại lượng thu được thu được tự trạng thái; M, C, D, g, JB/E, và τC lần lượt là ma trận khối lượng, ma trận lực Coriolis, ma trận lực cản thủy động, ma trận lực trọng trường, ma trận chuyển đổi từ hệ trục Body-fixed{B} sang hệ trục Earth-fixed {E}, và ma trận lực / mô-men điều khiển [30], [31].
Phương trình chuyển động của AUV:
Theo [30], [31], phương trình chuyển động động lực học phi tuyến của AUV như sau:
(3.3) |
Có thể bạn quan tâm!
-
Các Nghiên Cứu Về Điều Khiển Auv Trên Thế Giới -
Tổng Quan Về Mạng Nơ-Ron Nhân Tạo Trong Điều Khiển -
Điều Khiển Tự Động Dùng Mạng Nơ-Ron Nhân Tạo -
Mô Hình Tổng Quát Của Bộ Điều Khiển Nnc Huấn Luyện Trực Tuyến -
Các Phương Án Thích Nghi Cho Hệ Thống Điều Khiển Auv -
Đáp Ứng Hướng Đi Của Auv Khi Có Dòng Chảy (Tn3)
Xem toàn bộ 169 trang tài liệu này.
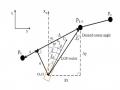
Trong trường hợp có xét vận tốc dòng chảy, ta được vector vận tốc tương đối là:
𝑉𝑟= 𝑉 − 𝑉𝑐, 𝑉𝑐= [𝑢𝑐, v𝑐, 𝑤𝑐, 0,0,0]𝑇
Phương trình (3.3) trở thành:
(3.4) |
Nếu chỉ giới hạn ở nước tĩnh trong hồ thì có thể bỏ qua ảnh hưởng của dòng chảy, ảnh hưởng của gió và của sóng. Phương trình chuyển động của AUV cuối cùng là:
(3.5) |
Trong đó:
- 𝑀 = 𝑀𝑅𝐵 + 𝑀𝐴: ma trận lực quán tính (tính cả quán tính chất lỏng).
- 𝐶(𝑉𝑟) = 𝐶𝑅𝐵(𝑉𝑟) + 𝐶𝐴(𝑉𝑟): ma trận lực hướng tâm Coriolis (tính cả quán tính chất lỏng).
- 𝐷(𝑉𝑟): ma trận lực cản.
- g(𝜂): vector trọng lực/lực đẩy Acsimet và moment (lực phục hồi).
- g0: vector trọng lực thêm vào để làm AUV cân bằng.
- 𝜏: vector lực điểu khiển đầu vào.
Lực và moment xuất phát từ bản thân vật rắn:
𝑀𝑅𝐵 = 𝑀𝑅𝐵𝑇 > 0, 𝑀̇ 𝑅𝐵 = 06×6 | (3.6) |
Theo tài liệu [31], ta có công thức của ma trận quán tính vật rắn (Rigid- body system inertial matrix) 𝑀𝑅𝐵 là duy nhất và thỏa mãn điều kiện sau:
Trong đó:
(3.7) |
sau:
Cũng theo tài liệu [31], ma trận Coriolis 𝐶𝑅𝐵(𝑉) thõa mãn điều kiện
(3.8) | |
0 0 0 0 0 0 0 0 0 𝐶 (𝑉) = 𝑅𝐵−𝑚(𝑦𝑔𝑞 + 𝑧𝑔𝑟) 𝑚(𝑦𝑔𝑝 + 𝑤) 𝑚(𝑧𝑔𝑝 − v) 𝑚(𝑥𝑔𝑞 − 𝑤) −𝑚(𝑧𝑔𝑟 + 𝑥𝑔𝑝) 𝑚(𝑧𝑔𝑞 + 𝑢) [ 𝑚(𝑥𝑔𝑟 + v) 𝑚(𝑦𝑔𝑟 − 𝑢) −𝑚(𝑥𝑔𝑝 + 𝑦𝑔𝑞) 𝑚(𝑦𝑔𝑞 + 𝑧𝑔𝑟) −𝑚(𝑥𝑔𝑞 − 𝑤) −𝑚(𝑥𝑔𝑟 + v) −𝑚(𝑦𝑔𝑝 + 𝑤) 𝑚(𝑧𝑔𝑟 + 𝑥𝑔𝑝) −𝑚(𝑦𝑔𝑟 − 𝑢) −𝑚(𝑧𝑔𝑝 − v) −𝑚(𝑧𝑔𝑞 + 𝑢) 𝑚(𝑥𝑔𝑝 + 𝑦𝑔𝑞) 0 −𝐼𝑦𝑧𝑞 − 𝐼𝑥𝑧𝑝 + 𝐼𝑧𝑟 𝐼𝑦𝑧𝑟 + 𝐼𝑥𝑦𝑝 − 𝐼𝑦𝑞 𝐼 𝑞 + 𝐼 𝑝 − 𝐼 𝑟 0 −𝐼 𝑟 − 𝐼 𝑞 + 𝐼 𝑝 𝑦𝑧 𝑥𝑧 𝑧 𝑥𝑧 𝑥𝑦 𝑥 −𝐼𝑦𝑧𝑟 − 𝐼𝑥𝑦𝑝 + 𝐼𝑦𝑞 𝐼𝑥𝑧𝑟 + 𝐼𝑥𝑦𝑞 − 𝐼𝑥𝑝 0 ] | (3.9) |
Vì chọn gốc tọa độ Ob trùng với trọng tâm của AUV, ngoài ra có thể coi như AUV đối xứng qua các mặt phẳng Oxy, Oyz, Oxz (vì vận tốc nhỏ) nên các ma trận 𝑀𝑅𝐵 và ma trận 𝐶𝑅𝐵(𝑉) trở thành:
(3.10) | |
𝑚 0 0 0 0 0 0 𝑚 0 0 0 0 0 0 𝑚 0 0 0 𝑀𝑅𝐵 =0 0 0 𝐼 0 0 𝑥 0 0 0 0 𝐼𝑦 0 [ 0 0 0 0 0 𝐼𝑧] | (3.11) |
Lực và moment thủy động lực học:
Các lực và moment này gồm 3 thành phần:
- 𝑀𝐴 : quán tính chất lỏng.
- 𝐶𝐴(𝑉𝑟) : Lực hướng tâm Coriolis khi xét tới quán tính chất lỏng.
- 𝐷(𝑉𝑟) : lực cản thủy động lực học (hydrodynamic damping).
Gọi 𝑇𝐴 là năng lượng thủy động lực học của dòng lưu chất, ta có được phương trình:
(3.12) |
Trong đó, ma trận 𝑀𝐴 = 𝑀𝐴𝑇 ≥ 0 là 1 ma trận quán tính 6x6:
(3.13) |
Với các giá trị trong ma trận là hệ số quán tính của chất lỏng. Ví dụ, lực quán tính chất lỏng Y theo trục y gây ra bởi gia tốc 𝑢̇ theo trục x được tính như sau:
(3.14) |
Theo [28], ma trận quán tính chất lỏng (added mass) phụ thuộc nhiều vào hình dạng của AUV. Bởi vì, ta giả sử rằng AUV đối xứng qua 3 mặt
phẳng và gốc của hệ tọa độ {b} đặt tại trọng tâm AUV nên ma trận 𝑀𝐴 trở thành:
(3.15) |
Các thông số này là hằng số khi AUV hoàn toàn chìm trong nước. Các giá trị này thường khó tìm và thường được chọn theo kinh nghiệm trong lân cận từ 10% - 100% giá trị từ ma trận 𝑀𝑅𝐵. Theo tìm hiểu một số thông số từ các AUV, có thể chọn các thông số quán tính chất lỏng ở ma trận 𝑀𝐴 bằng 50% giá trị từ ma trận 𝑀𝑅𝐵.
Đối với 1 vật thể cứng khi đi xuyên qua 1 chất lỏng lý tưởng, lực hướng
tâm Coriolis 𝐶𝐴(𝑉) có thể luôn được tham số hóa thỏa mãn điều kiện:
(3.16) |
Trong đó:
(3.17) |
Với:
𝑎1 = 𝑋𝑢̇ 𝑢 + 𝑋𝑣̇ v + 𝑋𝑤̇ 𝑤 + 𝑋𝑝̇𝑝 + 𝑋𝑞̇ 𝑞 + 𝑋𝑟̇ 𝑟
𝑎2 = 𝑌𝑢̇ 𝑢 + 𝑌𝑣̇ v + 𝑌𝑤̇ 𝑤 + 𝑌𝑝̇ 𝑝 + 𝑌𝑞̇ 𝑞 + 𝑌𝑟̇ 𝑟
(3.18) |
𝑏1 = 𝐾𝑢̇ 𝑢 + 𝐾𝑣̇ v + 𝐾𝑤̇ 𝑤 + 𝐾𝑝̇ 𝑝 + 𝐾𝑞̇ 𝑞 + 𝐾𝑟̇ 𝑟
𝑏2 = 𝑀𝑢̇ 𝑢 + 𝑀𝑣̇ v + 𝑀𝑤̇ 𝑤 + 𝑀𝑝̇ 𝑝 + 𝑀𝑞̇ 𝑞 + 𝑀𝑟̇ 𝑟
𝑏3 = 𝑁𝑢̇ 𝑢 + 𝑁𝑣̇ v + 𝑁𝑤̇ 𝑤 + 𝑁𝑝̇ 𝑝 + 𝑁𝑞̇ 𝑞 + 𝑁𝑟̇ 𝑟
Bởi vì, giả sử rằng AUV đối xứng qua 3 mặt phẳng và AUV di chuyển với vận tốc chậm nên ma trận 𝐶𝐴(𝑉) có thể được viết dưới dạng đơn giản sau đây:
(3.19) |
Lực cản thủy động lực học:
Vì trong thực tế rất khó để có thể xác định toàn bộ các hệ số để xác định các lực cản. Theo [28], xấp xỉ công thức như sau:
(3.20) |
Với:
𝑋𝑢, 𝑌v, 𝑍𝑤, 𝐾𝑝, 𝑀𝑞 , 𝑁𝑟: là thành phần tuyến tính của hệ số cản thủy động.
𝑋𝑢|𝑢|, 𝑌v|v|,, 𝑍𝑤|𝑤|, 𝐾𝑝|𝑝|, 𝑀𝑞|𝑞|, 𝑁𝑟|𝑟|: thành phần bậc hai của hệ số cản thủy động.
Lực phục hồi:
Gọi ∇ là thể tích của chất lỏng bị chiếm bởi AUV, g là gia tốc trọng trường, ρ là khối lượng riêng chất lỏng. Trọng lượng riêng W và lực đẩy Acsimet Archimet B là:
(3.21) |
Theo [5], công thức lực phục hồi được tính như sau:
(3.22) |
Trong đó:
(3.23) |
Suy ra được công thức:
(3.24) |
Với (𝑥𝑏, 𝑦𝑏 , 𝑧𝑏) là tọa độ của tâm lực đẩy Acsimet.
Để đơn giản trong quá trình tính toán, chọn 𝑊 = 𝐵 nên:
(3.25) |
Suy ra:
(3.26) |
Trọng lực thêm vào:
Đối với trọng lực được thêm để AUV ở trạng thái cân bằng theo ý muốn, theo [31] sẽ có công thức như sau:
(3.27) |
Mô hình điều động trong mặt phẳng độ sâu
Trong đề tài nghiên cứu này, để tập trung vào việc điều khiển riêng độ sâu của AUV, tác giả chỉ quan tâm đến mô hình điều động trong mặt phẳng độ sâu. Do đó phương trình động lực mặt phẳng độ sâu sẽ được sử dụng như là hàm truyền mô tả hệ thống. Đối với mô hình điều động trong mặt phẳng độ sâu, góc pitch (𝜃) của AUV sẽ được điều khiển. Do đó, có thể bỏ qua các biến trạng thái 𝑦, 𝜙, 𝜓, 𝜐, 𝑝, 𝑟 trong mặt phẳng nằm ngang, vậy nên phương trình động lực học của hệ thống được rút gọn thành (3.28) với các hệ số được mô tả trong bảng 4.1.
(3.28) |
trong đó: 𝐼𝑦𝑦 là moment quán tính quanh trục Y; 𝑀𝜃, 𝑀𝑞, 𝑀𝑞̇ là các hệ số thủy động lực học được mô tả trong bảng 4.1.
3.2 Mạng nơ-ron thích nghi trong điều khiển
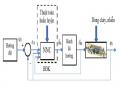
Trong [3] tác giả đề xuất phương pháp điều khiển thích nghi với mạng nơ-ron bằng lý thuyết thích nghi tương tác. Theo nghiên cứu này, các nơ-ron trong mạng được xem như các hệ thống con gọi là các thiết bị trong một hệ thống phức tạp. Phương pháp này tương tự như thuật toán lan truyền ngược nhưng không cần đến mạng lan truyền ngược để truyền ngược tín hiệu sai số. Mạng nơ-ron điều khiển thích nghi của một số hệ thống dùng phương pháp này được mô phỏng trong [3] và ứng dụng trong [8], [9] để minh họa tính khả thi và hiệu quả của phương pháp. Phần 3.2.1 sẽ mô tả tóm tắt thuật toán thích nghi tương tác áp dụng cho mạng nơ-ron để tạo thành bộ điều khiển nơ-ron thích nghi tương tác (Adaptive Neural Network by Adaptive Interaction - ANNAI).
3.2.1 Bộ điều khiển nơ-ron thích nghi tương tác
Tham khảo trong tài liệu [3] và sử dụng các ký hiệu dưới đây với i, j N
Oi Ii
i
wij
g(x)
O
d i
tín hiệu ra của nơ-ron thứ i; tín hiệu vào của nơ-ron thứ i;
giá trị ngưỡng của nơ-ron thứ i;
trọng số của liên kết từ nơ-ron thứ i đến nơ-ron thứ j; hàm kích hoạt của một nơ-ron;
giá trị đầu ra mong muốn của nơ-ron thứ i (đối với nơ-ron lớp
ra);
bước học,
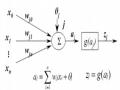
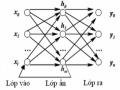
Mạng nơ-ron sẽ được mô tả như sau:
Iiwij Oji, (3.29)
jN