Động học:
Tổng kết lại những phần trên, ta được phương trình động học 6 DOF dưới dạng vector như sau:
𝜂̇ = 𝐽(𝜂)V
(1.7) |
Có thể bạn quan tâm!
-
Nghiên cứu điều khiển thích nghi cho robot lặn tự hành - 2 -
Tổng Quan Về Robot Lặn Tự Hành Auv (Autonomous Underwater Vehicle) -
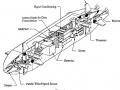
![Nghiên Cứu Auv Mô Hình Tại Trường Đh Bách Khoa Hà Nội [7]](https://tailieuthamkhao.com/uploads/2023/02/21/nghien-cuu-dieu-khien-thich-nghi-cho-robot-lan-tu-hanh-4-1-120x90.jpg)
Nghiên Cứu Auv Mô Hình Tại Trường Đh Bách Khoa Hà Nội [7] -
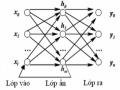
Tổng Quan Về Mạng Nơ-Ron Nhân Tạo Trong Điều Khiển -
Điều Khiển Tự Động Dùng Mạng Nơ-Ron Nhân Tạo -
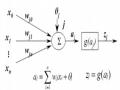
Wij O J I , (3.29)
Xem toàn bộ 169 trang tài liệu này.
Động lực học:
Phương trình chuyển động của vật rắn:
Theo định luật Newton cho vật rắn có khối lượng m, ta có phương trình cân bằng lực và moment như sau:
(1.8) | |
𝐼𝑏𝜔̇ 𝑏 + 𝜔𝑏 × (𝐼𝑏𝜔𝑏 ) + 𝑚𝑟𝑏 × (𝑣̇𝑏 + 𝜔𝑏 × 𝑣𝑏 ) = ɱ𝑏 𝑏/𝑛 𝑏/𝑛 𝑏/𝑛 𝑔 𝑏/𝑛 𝑏/𝑛 𝑏/𝑛 𝑏 | (1.9) |
{b}.
{b}.
Trong đó:
𝑏
𝑓𝑏 = [𝑋, 𝑌, 𝑍]𝑇: lực tác dụng qua tâm Ob được biểu diễn trong {b}.
𝑏
ɱ𝑏 = [𝐾, 𝑀, 𝑁]𝑇: moment đối với Ob được biểu diễn trong {b}.
𝑏/𝑛
𝑣𝑏 = [𝑢, v, 𝑤]𝑇: vận tốc dài của Ob đối với On được biểu diễn trong
𝑏/𝑛
𝜔𝑏 = [𝑝, 𝑞, 𝑟]𝑇: vận tốc góc của {b} so với {n} được biểu diễn trong
𝑇
𝑟𝑏 = [𝑥 , 𝑦 , 𝑧 ] : vector từ O
đến CG được biểu diễn trong {b}.
𝑔 𝑔 𝑔 𝑔 b
Từ trên ta suy ra phương trình các lực và moment trên AUV:
(1.10) |
𝐼𝑦𝑞̇ + (𝐼𝑥 − 𝐼𝑧)𝑟𝑝 − (𝑝̇ + 𝑞𝑟)𝐼𝑥𝑦 + (𝑝2 − 𝑟2)𝐼𝑧𝑥
+ (𝑝𝑞 − 𝑟̇)𝐼𝑦𝑧
+𝑚[𝑧𝑔(𝑢̇ − v𝑟 + 𝑤𝑞) − 𝑥𝑔(𝑤̇ − 𝑢𝑞 + v𝑝)] = 𝑀
𝐼𝑧𝑟̇ + (𝐼𝑦 − 𝐼𝑥)𝑝𝑞 − (𝑞̇ + 𝑟𝑝)𝐼𝑦𝑧 + (𝑞2 − 𝑝2)𝐼𝑥𝑦
+ (𝑟𝑞 − 𝑝̇)𝐼𝑧𝑥
+𝑚[𝑥𝑔(v̇ − 𝑤𝑝 + 𝑢𝑟) − 𝑦𝑔(𝑢̇ − v𝑟 + 𝑤𝑞)] = 𝑁
Với Ib là moment quán tính đối với gốc Ob , ta có:
(1.11) |
Với 𝐼𝑥, 𝐼𝑦, 𝐼𝑧 là momen quán tính đối với trục xb , yb, zb và 𝐼𝑥𝑦 = 𝐼𝑦𝑥, 𝐼𝑥𝑧
= 𝐼𝑧𝑥, 𝐼𝑦𝑧 = 𝐼𝑧𝑦 là momen quán tính ly tâm được định nghĩa như sau:
(1.12) |
𝑔
Nếu chọn gốc tọa độ Ob trùng với trọng tâm của AUV thì 𝑟𝑏 = [0,0 , 0]𝑇,
phương trình sẽ đơn giản hơn trong quá trình tính toán.
(1.13) |
Phương trình tổng quát của AUV khi độ sâu không đổi được viết lại
thành:
(1.14) |
Trong đó: 𝛿𝑠 là góc bánh lái ở đuôi của AUV, 𝑈 là vận tốc của AUV.
1.2 Tổng quan về điều khiển AUV hiện nay
1.2.1 Các nghiên cứu về điều khiển AUV trên thế giới
Trong lĩnh vực điều khiển tự động, các nhà khoa học thường có xu hướng tiếp tục nghiên cứu phát triển phương pháp điều khiển mới dựa trên phương pháp cũ để khắc phục những nhược điểm tồn tại hoặc tìm kiếm các phương pháp hoàn toàn khác không dựa trên phương pháp cũ đã có trước đây [5]. Điều này làm thúc đẩy mạnh mẽ các ứng dụng trong lĩnh vực điều khiển tự động ở phạm vi rộng.
Mặc dù có những bước tiến mạnh mẽ, nhưng cho đến giờ các phương pháp điều khiển mới vẫn chưa thay thế hoàn toàn các kỹ thuật phổ biến, như điều khiển PID truyền thống. Kể từ khi thuật toán điều khiển PID được kỹ sư người Mỹ gốc Nga Nicolas Minorsky áp dụng vào hệ thống máy lái tự động tàu thủy năm 1922 đến nay, đã có nhiều nghiên cứu về bộ điều khiển PID này được ứng dụng rộng rãi trong lĩnh vực điều khiển tự động kể cả việc ứng dụng trí tuệ nhân tạo [28]. Mặc dù vậy, bộ điều khiển PID vẫn chiếm hơn 90% ứng dụng trong các hệ thống công nghiệp [6].
Trong những năm gần đây, kỹ thuật điều khiển dùng mạng nơ-ron và hệ thống Logic mờ đã phát triển rất nhanh chóng. Nhiều hệ thống Logic mờ với các cách ứng dụng khác nhau đã được đề xuất và ứng dụng rộng rãi trong kỹ thuật [5], [6].
Bộ điều khiển PID thích nghi dựa trên việc điều hưởng các tham số KP, KI và KD bằng hệ thống Logic mờ thích nghi hoặc mạng nơ-ron nhân tạo được gọi là điều khiển PID mờ, PID nơ-ron được các nhà khoa học nghiên cứu ứng
dụng rộng rãi trong hệ thống công nghiệp như các công trình nghiên cứu của [11], [12], [13], [15], [16]. Hơn nữa, tính đơn giản là một trong những đặc trưng quan trọng của bộ điều khiển PID và các nhà thiết kế hệ thống đã giữ lại đặc điểm này. Các thuật toán được đề xuất thường không thay đổi cấu trúc của bộ điều khiển PID thông thường mà cố gắng sử dụng khả năng thích nghi của mạng nơ-ron hay hệ thống Logic mờ, hoặc kết hợp cả 2 kỹ thuật này.
Phát triển hệ thống điều khiển AUV là mục tiêu nghiên cứu của rất nhiều nhà khoa học. Một số công trình nghiên cứu thiết kế hệ thống điều khiển AUV tiêu biểu trước đây và trong thời gian gần đây như [11] – [22], [24] – [26], [29], [34-46], [48-55], [57-65]. Trong số các phương pháp ứng dụng kỹ thuật điều khiển với trí thông minh nhân tạo cho các phương tiện thủy, bên cạnh Logic mờ, mạng nơ-ron đã chứng tỏ được khả năng tốt, hiệu quả và khả thi khi tham gia điều khiển các hệ thống phức tạp, giúp nâng cao chất lượng điều khiển.
Các tài liệu về những nghiên cứu từ giai đoạn 1990 đã từng bước hoàn thiện mô hình toán học phức tạp của AUV và phương án điều khiển. Được tham khảo trong nhiều tài liệu là mô hình động học AUV trong [26], [31]. Aage C. và Smitt L.W. (1994) trình bày đặc tính thủy động học của AUV dạng dẹt [17] và các kết quả mô phỏng cho đối tượng này [18]. R. Cristi, F.A. Papoulias và A.J. Healey (1990) nghiên cứu điều khiển thích nghi cho hoạt động lặn của AUV [19]. Năm 1992 Y. Nakamura và S. Savant trình bày điều khiển phi tuyến AUV theo đường đi mong muốn [20] và trong [21] nghiên cứu các cảm biến dùng cho AUV phục vụ nghiên cứu biển và đại dương.
Các nghiên cứu về hoạt động của AUV vùng nước sâu cũng được trình bày trong [22] của Bjerrum A. (1997) và [23] của Chance T.S. và các cộng sự (2000). N.E. Leonard nghiên cứu về tổng hợp bộ điều khiển và phương pháp thích nghi cho đối tượng AUV (1995) trong [25]. Năm 1994 T. Prestero trình bày mô phỏng hoạt động của REMUS AUV 6 bậc tự do, tổng hợp các thông số thủy động học giúp cho mô hình có thể ứng dụng cho các hoạt động mô phỏng [27].
Năm 1990, D. Yoerger và cộng sự trình bày nghiên cứu về ảnh hưởng của tính năng hệ động lực đến hoạt động của AUV và đưa vào tính toán thiết kế hệ thống điều khiển [41]. Các nghiên cứu về Phoenix AUV được D. Brutzman cùng cộng sự (1998) trình bày trong [45], [48] và D. Davis (1996) trình bày trong [46]. Năm 1996 D. Marco và cộng sự nghiên cứu điều khiển AUV trong cả chuyển động và thực hiện các nhiệm vụ dưới nước một cách đồng thời, bước đầu giải quyết điều khiển các vấn đề phức tạp của AUV. Trong luận án Tiến sĩ (1994) D. Brutzman đã giới thiệu phương pháp mô phỏng với mô hình ảo để nghiên cứu AUV [50]. Trong nghiên cứu (1999) của mình M. Sfakiotakis và cộng sự tìm hiểu mô hình bơi của robot cá nhằm ứng dụng cho AUV loại này [56]. Năm 1993 A.J. Healey và D. Lienard giới thiệu kỹ thuật điều khiển dạng trượt nhiều biến áp dụng cho điều khiển hướng và độ sâu AUV [95].
Từ đầu thập niên đầu tiên của Thế kỷ 21 đến nay với khoảng thời gian 20 năm, các nghiên cứu về AUV cũng phong phú và phát triển mạnh mẽ hơn. Mô hình toán học đối tượng dần được hoàn thiện hơn, các phương pháp điều khiển hiện đại được ứng dụng phổ biến.
Fossen (2001) trình bày rất hệ thống về mô hình thủy động học và điều khiển các phương tiện thủy, trong đó có AUV kể cả nguyên lý điều khiển dẫn đường cho các phương tiện [30]. Năm 2001, T. Prestero tiếp tục trình bày mô phỏng hoạt động của REMUS AUV 6 bậc tự do, tổng hợp các thông số thủy động học giúp cho mô hình có thể ứng dụng cho các hoạt động mô phỏng tại một ấn phẩm khác của MIT [59]. McEwen và Streitlien (2001) nghiên cứu mô hình hóa và điều khiển AUV có chiều dài thay đổi [71]. Các tác giả trình bày phương pháp mô hình hóa, tổng hợp hệ thống điều khiển vòng kín cho AUV đối với hướng đi, độ sâu.
Năm 2003 W. Naeem và cộng sự nghiên cứu thuật toán điều khiển LQG/LTR cho AUV với hệ thống dẫn đường lai cho nhiệm vụ bám theo đường dây cáp ngầm dưới nước [72]. Bộ điều khiển tuyến tính “Linear quadratic Gaussian controller with loop transfer recovery” (LQG/LTR) có
tính ổn định tốt điều khiển AUV ở các tốc độ khác nhau. D. Xu và các cộng sự (2000) trình bày bộ điều khiển phi tuyến cấu trúc thay đổi 2 chế độ cho AUV [96], trong đó bộ điều khiển áp dụng cho hệ SISO cho từng chuyển động riêng của AUV đảm bảo tốc độ đáp ứng tối ưu, độ quá điều khiển nhỏ, không có sai số tĩnh, không dao động. Huanan Yu và Jun Dai giới thiệu BĐK mờ tinh chỉnh bằng thuật toán di truyền ứng dụng cho AUV [100], trong đó BĐK mờ được tự động chọn tham số thông qua một thuật toán di truyền.
Trong nghiên cứu [107] năm 2001, vấn đề nhận dạng mô hình AUV được P. Ridao và cộng sự thực hiện. Các tác giả sử dụng phương pháp bình phương nhỏ nhất tính toán nhận dạng các thông số AUV riêng biệt theo từng bậc tự do, với giả thiết tốc độ AUV chậm. Năm 2005 A. Thomas và các cộng sự trình bày nghiên cứu về hệ động lực phản lực nước cho phương tiện ngầm cỡ nhỏ [35]. Bài báo này đề xuất hệ thống động lực phản lực nước làm tăng khả năng điều động, xoay trở cho AUV. Cũng vào năm 2005 này, X. Deng và S. Avadhanula giới thiệu phương tiện ngầm siêu nhỏ chuyển động bằng vây lắc [40]. Bài báo đã phân tích thiết kế hệ thống và tính toán các lực cho hệ động lực này. Cùng thời điểm, M. Krieg và các công sự (2005) công bố nghiên cứu về tối ưu đặc tính đẩy cho động cơ phản lực nước ứng dụng vào điều động ở tốc độ thấp cho AUV [44]. Các tác giả đã thiết kế và thử nghiệm nguyên mẫu cho hệ động lực đẩy này.
Trong nghiên cứu của L.A. Gonzalez (2004) tác giả trình bày các vấn đề về mô hình hóa và điều khiển AUV [109]. K. Mohseni (2004) trình bày về động cơ đẩy phản lực nước theo nhịp xung cho chuyển động của AUV cỡ nhỏ [57], với khả năng điều động hoặc định vị cho AUV. Cũng năm 2004 A. Healey nghiên cứu về tránh va cho AUV REMUS khi đang chuyển động theo địa hình đáy [52]. Bài báo cho thấy hệ thống điều khiển có khả năng giúp AUV tránh vật cản bất ngờ do sự thay đổi đột ngột của địa hình đáy. Tiếp tục ứng dụng cho AUV REMUS, D. Hemminger (2005) cũng trình bày nghiên cứu điều khiển tránh va trong mặt thẳng đứng cho AUV này sử dụng tín hiệu
siêu âm phía trước [53]. Xu hướng về AUV sinh học được P.R. Bandyopadhyay trình bày trong [37] cũng vào năm 2005.
T.H. Furukawa (2006) trong luận án của mình đã trình bày về thuật toán bám đường đi và tránh va chạm cho AUV sử dụng tín hiệu siêu âm phía trước mũi [51]. Năm 2007 R. Prasanth Kumar và các cộng sự đề xuất điều khiển bền vững AUV theo quỹ đạo dùng luật điều khiển trễ thời gian [33]. Bộ điều khiển này dựa trên việc ước lượng trực tiếp tính năng động học của AUV, các thí nghiệm mô phỏng chứng minh sự hiệu quả của luật điều khiển. Xu Yuru và cộng sự năm 2006 và 2007 trình bày sự phát triển công nghệ AUV
[92] và triển vọng tương lai [93]. L. Lapierre và D. Soetanto (2007) đã nghiên cứu về điều khiển phi tuyến bám quỹ đạo cho AUV [112], trong đó bộ điều khiển được xây dựng dựa trên lý thuyết Lyapunov và kỹ thuật phản hồi tín hiệu.
Năm 2008 M. Krieg và K. Mohseni giới thiệu nghiên cứu về đặc tính động lực đẩy của hệ động lực mới, sự dụng chuyển động dạng xung tạo ra phản lực cho AUV chuyển động ở tốc độ thấp [43]. P. Patron và cộng sự (2008) nghiên cứu về chẩn đoán và chỉnh sửa kế hoạch thích nghi cho sửa lỗi trong AUV [54]. Cũng năm 2008 này, P. Jantapremjit và P. A. Wilson trình bày về điều khiển AUV bám quỹ đạo dựa trên hệ thống dẫn đường [111]. Trong bài báo này kỹ thuật dẫn đường bám theo quỹ đạo bằng thuật toán Line- of-Sight được áp dụng.
Năm 2009 O. Yildiz và cộng sự có bài nghiên cứu hệ thống hóa các vấn đề về điều khiển chuyển động cho AUV [79]. B. Regardt (2009) cũng trình bày nghiên cứu về mô hình hóa và mô phỏng AUV [32], trong đó mô hình toán học cho AUV được thực hiện cả về mô hình tuyến tính và phi tuyến được đề xuất. P. Krishnamurthy và cộng sự (2009) nghiên cứu về AUV sinh học 6 bậc tự do, công bố các kết quả mô phỏng và thực nghiệm [36]. Năm 2010 E. Lee nghiên cứu về thiết kế robot dạng cá, mềm và tự hành [58].
Thập niên vừa qua, các nghiên cứu cùng lĩnh vực này cũng phát triển mạnh mẽ, đa dạng và áp dụng các nền tảng kiến thức mới nhất đối với mô
phỏng và điều khiển AUV. Năm 2011 A. Mazumdar và H.H. Asada nghiên cứu về AUV sử dụng van “highbandwith coanda-effect” hoạt động ở tốc độ chậm [34]. E. Miguelanez và cộng sự (2011) nghiên cứu nâng cao khả năng nhận thức tình huống cho AUV dựa trên “semantic-knowedge” [55]. G. Martins và cộng sự (2011) nghiên cứu AUV thông minh với công nghệ XMOS [60]. M. Mazumdar và cộng sự (2012) trình bày nghiên cứu về mẫu AUV nhỏ dùng cho khảo sát đường ống nhà máy điện hạt nhân [38]. Cũng trong năm này, M. Mazumdar và H. Asada trình bày tiếp nghiên cứu điều khiển hệ van cho hệ động lực của AUV có khả năng điều động cao [42]. Năm 2013 F. Giorgio và cộng sự trình bày nghiên cứu về hệ động lực xoáy cho mẫu AUV thân mềm mới [39]. F. Rezazadegan và K. Shojaei (2013) nghiên cứu điều khiển thích nghi 6 bậc tự do cho AUV với các hàm bão hòa [84]. Năm 2014 B. Geranmehr và S.R. Nekoo đề xuất điều khiển độc lập trạng thái theo điểm đặt và theo quỹ đạo cho AUV trong mặt phẳng ngang [83].
Cũng vào năm 2014 A. Adhami-Mirhosseini và cộng sự công bố nghiên cứu về điều khiển tự động theo địa hình đáy cho AUV [113]. J. Ghommam và M. Saad (2014) trình bày điều khiển phản hồi và bám quỹ đạo thích nghi cho nhóm các AUV trong mặt phẳng ngang [121]. X. Qi (2014) nghiên cứu về điều khiển thích nghi quỹ đạo cho nhiều AUV [117].
Năm 2015 M.H. Khodayari và S. Balochian đăng tải nghiên cứu về mô hình hóa và điều khiển hướng đi, độ sâu AUV bằng bộ điều khiển PID mờ tự thích nghi [69]. J.E. Ruiz Duarte và J.E. Loukianov (2015) đã trình bày nghiên cứu về điều khiển độ sâu AUV với điều khiển trượt bậc cao hơn [77]. Cũng năm 2015 B. Geranmehr và S.R. Nekoo nghiên cứu về điều khiển phi tuyến tối ưu AUV với phương trình trạng thái phụ thuộc Riccati [81]. Trước đó hai tác giả này cũng công bố (2014) về điều khiển phi tuyến tối ưu độ sâu AUV [82]. K. Mukherjee và cộng sự (2015) đề xuất điều khiển bám quỹ đạo cho AUV với kỹ thuật trễ tín hiệu đầu vào [97]. M. Kim và cộng sự (2015) nghiên cứu về bộ điều khiển trượt tích phân điều động chính xác cho AUV trong điều kiện nhiễu ngoại cảnh tác động [114].