Ma Trận Thí Nghiệm Kế Hoạch Trung Tâm Hợp Thành Với Hai Yếu Tố Ảnh Hưởng

e

ước lượng bởi S2 . Sự khác biệt không còn trong phạm vi sai số ngẫu nhiên

nữa, vì thế ngoài sai số theo nhiễu, nguyên nhân khiến sai số thống kê đó vượt trội số hệ thống sai lệch bổ sung do sự sai lệch không tương thích của mô hình so với đối tượng nghiên cứu.

Trong trường hợp này để có mô hình tương thích có thể chọn các giải pháp sau:

+ Phức tạp hóa mô hình bằng cách nâng bậc cao hơn.

+ Lập lại thực nghiệm với khoảng và mức biến thiên của thông số vào nhỏ hơn.

e. Xây dựng đồ thị ảnh hưởng của các yếu tố đầu vào đến thông số đầu ra

Dựa vào mô hình thực nghiệm thu được ta có thể xây dựng đồ thị ảnh hưởng của các thông số đầu vào X đến các thông số đầu ra là chi phí năng lượng riêng và năng suất của máy phay.

2.5.3. Thực nghiệm đa yếu tố

Để sử dụng phương pháp thực nghiệm đa yếu tố cần có các điều kiện [8]

sau:

+ Kết quả thông số ra phải tập trung cao, nghĩa là khi lặp lại nhiều lần

cùng một thí nghiệm thì giá trị thu được không sai lệch quá lớn.

+ Các yếu tố ảnh hưởng phải điều khiển được và chúng phải độc lập với nhau.

+ Mối liên hệ giữa các thông số tối ưu và các yếu tố ảnh hưởng được thể hiện bởi các phương trình và đáp ứng các điều kiện:

- Phải là hàm khả vi.

- Chỉ có một cực trị trong khoảng các yếu tố biến thiên.

Phương pháp quy hoạch thực nghiệm đa yếu tố được thực hiện theo các bước sau:

- Chuẩn bị dụng cụ đo, máy móc thiết bị thí nghiệm.

- Chọn phương án thích hợp cho thí nghiệm.

- Tổ chức thí nghiệm.

- Gia công số liệu thí nghiệm.

Phân tích và giải thích kết quả nhận được bằng thuật ngữ của các lĩnh vực khoa học tương ứng.

a. Chọn phương án quy hoạch thực nghiệm và lập ma trận thí nghiệm

Căn cứ vào kết quả thực nghiệm đơn yếu tố. Nếu kết quả thực nghiệm đơn yếu tố cho ta quy luật tương quan phi tuyến thì có thể bỏ qua việc tiến hành thực nghiệm bậc 1 và thực nghiệm theo phương án quy hoạch bậc 2.

Trong số các kế hoạch thực nghiệm thì kế hoạch trung tâm hợp thành là kế hoạch xuất hiện sớm nhất, nhưng hiện nay vẫn được ứng dụng rộng dãi trong nghiên cứu.

Tổng số các thí nghiệm cần thực hiện:

Trong đó:

N= 2k + Nα + N0

2k - Các thí nghiệm phần hạt nhân.

k- Các thông số ảnh hưởng, k =2 22 = 4 Nα- Các thí nghiệm ở mức sao.

No- Các thí nghiệm ở trung tâm

(2.23)

Biến thiên của các yếu tố trong vùng thí nghiệm gồm các mức cơ sở, mức trên và mức dưới, các giá trị này được chọn dựa vào phân tích kết quả đơn yếu tố.

Trong các mức khác nhau của yếu tố X i quan trọng nhất là mức cơ sở Xio được xác định theo công thức.

Xi0 = ( Ximin  Ximax )/2 (2.24)

Sau cùng là khoảng biến thiên của các yếu tố X.

e  X  X0  X0  X

(2.25)

i imix i i imin

Để chuyển từ giá trị tự nhiên sang dạng tọa độ.

xi = ( X i - Xio )/ e1

Trong đó: xi- Giá trị mã.

Xi- Giá trị thực của yếu tố thứ i.

(2.26)

Ở dạng mã mức dưới của mỗi yếu tố có giá trị (-1) mức cơ sở có giá trị 0, còn mức trên cơ sở có giá trị (+1).

Để làm cơ sở cho khâu tổ chức thí nghiệm và xử lý số liệu sau này ta lập bảng đối chiếu giữa các giá trị thực và dạng mã cho từng yếu tố (bảng 2.1) và xây dựng ma trận thí nghiệm (bảng 2.2) theo nguyên tắc các thí nghiệm hoàn toàn độc lập.

Bảng 2.1. Mã hoá các yếu tố ảnh hưởng

Các yếu tố

Mức

biến thiên

Mã hóa	X1	X2
Mức trên	+1
Mức cơ sở	0
Mức dưới	-1
Khoảng biến thiên	0

Có thể bạn quan tâm!

• Tình Hình Sử Dụng Và Nghiên Cứu Máy Phay Kim Loại Ở Trong Nước
• Đối Tượng, Phạm Vi Và Giới Hạn Nghiên Cứu
• Nội Dung Của Phương Pháp Qui Hoạch Thực Nghiệm
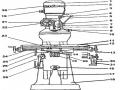
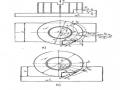
• Cấu Tạo, Nguyên Lý Hoạt Động Máy Phay Vạn Năng Tum20Vs
• Những Nhân Tố Ảnh Hưởng Đến Chi Phí Năng Lượng Riêng Khi Phay
• Ảnh Hưởng Của Tốc Độ Cắt Tới Chi Phí Năng Lượng Riêng Và Độ Nhám Bề Mặt

Xem toàn bộ 91 trang tài liệu này.

Bảng 2.2. Ma trận thí nghiệm kế hoạch trung tâm hợp thành với hai yếu tố ảnh hưởng

STT

X1	X2
1	-1	-1
2	+1	-1
3	-1	+1
4	+1	+1
5	-1	0
6	+1	0

7

0	+1
8	0	-1
9	0	0

b. Tiến hành thí nghiệm

Tiến hành các thí nghiệm theo ma trận đã lập. Sau khi thực hiện các thí nghiệm theo ma trận với số lần lặp lại của từng thí nghiệm m, chúng tôi sử dụng chương trình xử lý số liệu đa yếu tố OPT của Mỹ đã được chép bản quyền và lưu hành tại Viện cơ điện nông nghiệp Việt Nam để kiểm tra.

c. Xác định mô hình toán học

Hàm mục tiêu được biểu thị bằng các mô hình toán là phương trình hồi quy bậc 2 với dạng chung là [8]:

Y = b0

k

+ bx1 i l

k

+ 

il

K

bif

il

K

x

i

xi xf +bij 2

il

(2.27)

Trong đó: k – Yếu tố ảnh hưởng. Các hệ số:

X

N _ N N

b0 = a



u1

y - p 

i1

2

iu

u1

yu (2.28)

N

bi = e X iu yu

u1

(2.29)

N

bij = g X ui

u1

X ju Yu

(2.30)

N K N N

b = c X2yu+ d X yu- P Y (2.31)

ji iu

u 1

i l

ju

u l

u l

Trong chương trình máy tính các hệ số: a, b, c, d, e, p đã được tính sẵn nhờ xác định bo, bi, bii, bij và mô hình toán học được xác định.

d. Kiểm tra tính đồng nhất của phương sai

Kiểm tra tính đồng nhất của phương sai theo tiêu chuẩn Kohren, nếu

Gtt < Gb thì giả thiết H0

không mâu thuẫn với số liệu thí nghiệm. Phương sai

ở các thí nghiệm được coi là đồng nhất. Điều này cho phép coi cường độ nhiễu là ổn định khi thay đổi các thông số y trong thí nghiệm.

e. Kiểm tra mức ý nghĩa của các hệ số hồi qui

Các hệ số hồi qui bo, bi, bii, bij của phương trình sẽ được kiểm tra mức ý nghĩa theo tiêu chuẩn Student, trước khi tính phương sai của các hệ số hồi qui [8].

S

2

b0

S

2

bii

= a S 2

y

y

= (c+d) S 2

(2.32)

(2.33)

S 2 = e S 2 (2.34)

bi

S

2

bij

y

S

y

= g 2

(2.35)

S

y

Ở đây 2 là phương sai thực nghiệm.

S 2 = 1

N my

2

(2.36)

N

y

mu1

u 1

(Y - Yu )

u 1 j 1

Hệ số hồi qui có nghĩa khi:

s2

b0

|b0| > ± t

(2.37)

S2

bi

|bi| > ± t (2.38)

S2

bij

|bij| > ± t (2.39)

S2

bii

|bii| > ± t (2.40)

t- Giá trị chuẩn Student tra bảng thống kê với mức ý nghĩa α= 0,05 và bậc tự do γ= N(m-1).

Nếu hệ số

bi nào đó được tính theo công thức (2.28÷2.31) mà các giá trị

thỏa mãn các điều kiện (2.37 ÷ 2.40) thì có thể bỏ qua trong phương trình hồi quy.

g. Kiểm tra tính tương thích của phương trình hồi quy

Sau khi đã loại bỏ một số hệ số bi không có nghĩa khỏi mô hình (2.27) ta được phương trình hồi qui thực nghiệm. Chúng cần phải được kiểm tra theo tiêu chuẩn Fisher.

Ftt

m.S

2

S

=

2

e

(2.41)

N ^

2

mu

(yu

 yu )

S2=u 1

N  k

(2.42)

N mu

2

(yui

 yu )

e

S 2=u 1 i1

N

(2.43)

N

mu N

u 1

Fb với các bậc tự do γ1=N-k*; γ2=N(m-1) được tra bảng [8]. Trong đó k*- Số các hệ số hồi qui.

Nếu

Ftt < Fb

thì mô hình tương thích, nếu

Ftt > Fb

thì mô hình không

tương thích. Trong trường hợp này để có mô hình tương thích có thể chọn các giả pháp sau:

+ Phức tạp hóa mô hình bằng cách nâng bậc cao hơn.

+ Lập lại thực nghiệm bậc hai với mức biến thiên của các thông số đầu vào nhỏ hơn.

h. Tính lại các hệ số hồi qui

Nếu trong mô hình có một số hệ số vô nghĩa, chúng bị loại bỏ khỏi mô hình. Các hệ số còn lại liên quan phụ thuộc với chúng cần tính lại:

ii

+ Khi loại bỏ bậc tự do b0 thì hệ số bii mới ký hiệu b* .

b =

ii

* bii +

p

a b0 (2.44)

Một số hằng số bổ trợ cũng thay đổi theo cần tính lại sau đó kiểm tra lại các hệ số mới.

a* =

p* = 0 (2.45)

d * = d -

p2 (2.46)

a

C * = c (2.47)

Khi bỏ một số m hệ số

bii

1≤ m < n-1

Các hệ số:bj, bj,... không phải tính lại vì không liên quan phụ thuộc với

bij.

Chỉ tính các hệ số bij

còn lại và

b0 .

0

b* =

a* Y -

N

u

u1

* 2

N

X

P 

iu

u1

yu (2.48)

bii =

c* 

N

u1

X ui

y + d *

n



j1

N

X ju u1

y - P*

N

y

u1

(2.49)

Trong đó: X y = 0 (2.50)

N

2

iu

u1

a* = ( a - m e ) P*

(2.51)

p g

C * = c; d* =

p.d p

(2.52)

Sau khi loại bỏ các hệ số vô nghĩa và tính lại các hệ số khác không cần tính mức ý nghĩa của các hệ số mới theo đúng qui trình. Nếu mô hình trở lên không tương thích, bắt buộc sử dụng mô hình ban đầu.

i. Kiểm tra khả năng làm việc của phương trình hồi qui

Mô hình hồi qui được xác định nhằm mục đích dự báo giá trị hàm y tại các tọa độ được quan tâm, giải bài toán tối ưu. Ý nghĩa của phép kiểm tra là cho phép khẳng định mô hình có thực sự phản ánh ảnh hưởng của các yếu tố đến hàm chỉ tiêu hay không. Nếu mô hình có khả năng làm việc thì giá trị dự báo Y ở tọa độ nào đó là chính xác, có sai số nhỏ hơn ít nhất 2 lần so với việc gắn cho tọa độ đó là giá trị trung bình y tính theo toàn bộ số thí nghiệm.

y= 1 N

y = 1Ny

(2.53)

,

u

Nm u1

ud

u1 N u1

Nếu mô hình được coi là có khả năng làm việc (là hữu ích) trong sử dụng để dự báo hệ số đơn định R2 ≥0,75.

R 2 = 1-

m(N K* )S 2 N(m 1)s2

e

N

(2.54)

m(YuY ) N(m i)S

2 2

e

e

u1

Trong đó: m- Số lần lặp của mỗi thí nghiệm;

K*- Số các hệ số của phương trình hồi qui;

k. Chuyển phương trình hồi quy về dạng thực

Để mô tả sự ảnh hưởng của các thông số nghiên cứu đến các chỉ tiêu quan tâm cần đưa phương trình hồi quy về dạng thực với các biến là các thông số tự nhiên có thứ nguyên.

Thay công thức (2.26) vào phương trình hồi quy dạng mã ta được

n n n

Y =a0 +

ai xi aij Xi Xj

(2.55)

i1

i1

j1

Các hệ số a0, ai, aij có thể xác định theo hệ số hồi quy dạng mã:

n

a = b - 

bi x0i



bij x0i x0 j

(2.56)

0 0

i1

1 i

n

n

i1 j1

ij

j

=

a



bi -

i

bij -

ij

2bij

2 0 j



X

i

i≠j (2.57)

aij

2b

= ij



(2.58)

i j



a = 2bil

(2.59)

il 2

i

ε- Hệ số chuyển đổi;

Xi- Giá trị tự nhiên của các thông số.