Lý thuyết xác suất và thống kê toán

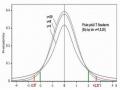
d) Gọi n là số xe ô tô gara cần có. Ta cần tìm n sao cho:

P{X > n} < 0,2  P{X ≤ n} > 0,98

Vì P{X ≤ 4} = 0,947 ; P{X ≤ 4} = 0,983

Suy ra: n = 5.

Ví dụ 2.22. Môt

lô cây hoa giống có 10000 cây, xác suất mỗi cây không ra hoa là

0,001. Tìm xác suất để trong lô cây giống đó có 3 cây không ra hoa ; có nhiều nhất 5 cây không ra hoa.

Giải

Ta thấy: p = 0,001 là khá bé và n = 10000 là khá lớn , cho nên có thể thay phân phối Nhi ̣thứ c bằng phân phối Poisson với  np = 10.

Ta có:

Xác suất để trong lô cây giống có 3 cây không ra hoa là:

P{X = 3} =

103

e10

Xác suất để trong lô cây giống có nhiều nhất 5 cây không ra hoa là:

P{X ≤ 5} =



k0

10k

e10

b. Định lý. Giả sử X ~ P(). Khi đó:

EX = VX =  ; modX = []

Ví dụ 2.23. Trong 1 cuốn sách có 1000 trang có 100 lỗi in sai. Tính xác suất để:

a) Khi mở ngẫu nhiên 1 trang không có lỗi nào,

b) Khi mở ngẫu nhiên 3 trang có đúng 2 lỗi in sai.

Giải

a) Gọi X = “số lỗi in sai trong 1 trang”.

X có phân phối Poisson với tham số 

100

1000

 0,1

Suy ra

P X 0e0,1  0,9048

b) Gọi Y = “số lỗi in sai trong 3 trang”.

Y có phân phối Poisson với tham số  3 100

1000

 0, 3 .

Suy ra

0,32 e0,3



P Y  2  0, 0333

2.4.3. Phân phối chuẩn

Phân phối chuẩn có một vai trò, vị trí rất quan trọng trong lý thuyết xác suất và trong thống kê cũng như ứng dụng trong thực tế, trong các lĩnh vực khoa học đời sống khác nhau.

a. Định nghĩa

Biến ngẫu nhiên liên tục X được gọi là có phân phối chuẩn với tham số  và 2

( >0) nếu hàm mật độ xác suất của nó có dạng:

x2

f(x) = Ký hiệu: X ~ N( , 2)

1

2



22

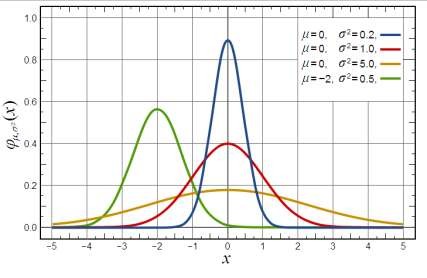
Hình 2.3: Phân phối chuẩn

Trường hơp

đă c

biêṭ nếu μ = 0 và

2 = 1 thì X được gọi là có phân phối chuẩn

tắc, ký hiệu là Ν0, 1. Khi đó hàm mâṭ đô ̣và hàm phân phối tương ứ ng có daṇ g :



1 x 1 x t

f(x) =e 2

2

và (x) = e

2

2 dt



1 x t

Hàm số (x) = e

2

2 dt

còn được gọi là hàm Laplace.

Chú ý:

2

t 2

1) Ta công nhận tích phân: e



2 dt 



1 0

t2

(tích phân này gọi là tích phân Euler)

(0)  e

2

2 dt  0,5

2) Từ phân phối chuẩn daṇ g tổng quát chuyển về daṇ g phân phối ch uẩn tắc bằng cách

đổi biến: Y = X 



Khi đó: nếu X ~ N(μ , σ) thì Y ~ N(0 , 1)

x (t)2

x

1

u2

x 

 P(X < x) = e

2dt

= e

2 du = 

22

 P(a ≤ X < b) = b 

-a 





3) Mối quan hệ giữa phân phối nhị thức và phân phối chuẩn: Cho X  B (n, p). Khi n khá lớn, p không quá lớn và không quá bé, ta có:

P(X = k) =

Ckpk1 pnk  1 f k  np 

np(1 p)

n 



k k nk

 k  np  k  np 

np(1 p)

P (k1  X  k2) =

Cn p 1 p

21

kk1

trong đó f là hàm mật độ Gauss, Φ là hàm Laplace



Do đó, khi n khá lớn và p không quá lớn và không quá bé thì X có xấp xỉ phân phối chuẩn, tức là X  N(, 2), trong đó

 = np , 2 = np(1 – p).

4) Cách tra bảng Laplace (bảng 3) như sau: Bài toán 1: Cho x tìm (x)

* Trường hợp x ≥ 0:

− Nếu x0  bảng sao cho x = x0 , thì ta có ngay (x) = (x0)

− Nếu x không có trong bảng, thì ta tìm cận x1, x2 trong bảng gần x nhất: x1 < x

< x2

+ Nếu |x – x1| < |x – x2| thì (x) ≈ (x1)

+ Nếu |x – x1| > |x – x2| thì (x) ≈ (x2)

* Trường hợp x < 0:

Theo trên ta tra bảng tìm (−x). Sau đó ta có (x) = 1 − (−x).

Bài toán 2: Cho y  (0, 1), tra bảng tìm x thoả (x) = y.

* Trường hợp y ≥ 0.5:

− Nếu x0  Bảng, (x0) = y, thì ta có ngay x = x0.

− Nếu y không có trong bảng, thì ta tìm cận y1, y2 trong bảng gần y nhất: y1 < y

< y2 và có (x1) = y1, (x2) = y2 . Khi đó:

+ Nếu |y – y1| < |y – y2| thì x ≈ x1

+ Nếu |y – y1| > |y – y2| thì x ≈ x2

* Trường hợp y < 0.5:

Tra bảng tính z = −1(1 − y) như trên, sau đó đặt x = −z.

Ví dụ 2.24.

a) Tính (0.74); (0.75); (0.746).

Tra bảng 3: muốn tính (0.74) dóng hàng “0.7” và cột “4” ta gặp 0.7704 nên:

(0.74) = 0.7704;

Tra bảng tương tự: (0.75) = 0.7734;

Ta có: 0.746 không có trong bảng

nhưng |0.746 – 0.74| = 0.006 > |0.746 – 0.75| = 0.004

nên ta lấy gần đúng: (0.746) = 0.7734 b) Tính −1(0.9128); −1(0.9115); −1(0.9131);

Tra bảng ta có:

−1(0.9115) = 1.35; −1(0.9131) = 1.36;

Ta có: |0.9128 – 0.9115| = 0.0013 > |0.9128 – 0.9131| = 0.0003

nên lấy gần đúng:

−1(0.9128) ≈ −1(0.9131) = 1.36

b. Định lý. Cho X là biến ngẫu nhiên có luật phân phối chuẩn N(μ,2) thì: EX = μ ; VX = σ2

ModX = μ ; MedX = μ

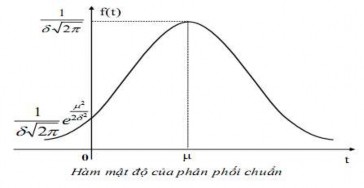
Hình 2.4: Hàm mật độ của phân phối chuẩn

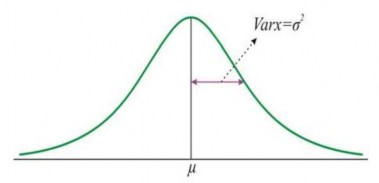
Hình 2.5: Độ lệch tiêu chuẩn

c. Mệnh đề. Cho X là biến ngẫu nhiên có luật phân phối chuẩn N(μ,2). Với α > 0, ta có xác suất:

Chứng minh:

P(|X − μ| < α) = 2.(α/) − 1

Ta có: P(|X − μ | < α) = P(−α/ < (X − μ)/ < α/)

= (α/) − (−α/) = 2.(α/) − 1

Ví dụ 2.25. Người ta tiện một loại chi tiết có độ dài μ. Biết độ dài X của chi tiết tuân theo luật phân phối N(μ, ) với  = 0.2cm.

a) Hãy tính xác suất để độ dài chi tiết không lệch quá μ dung sai là 0.3cm.

b) Muốn đảm bảo tỉ lệ phế phẩm không quá 5% thì phải chọn dung sai α bằng bao nhiêu ?

Giải

a) Xác suất cần tính là:

P(|X − μ | < 0,3) = 2.(0,3/0,2) – 1 = 2.(1,5) – 1

= 2 . 0,9332 = 0.8664

Như vậy tỉ lệ phế phẩm là 1 – 0,8664 = 13%.

b) Dung sai α phải thoả mãn:

P(|X − μ | < α) ≥ 0.95

 2.(α/0,2) - 1 ≥ 0,95

(α/0,2) ≥ 0.975

 α ≥ 0,2 . −1(0,975)

Tra bảng ta có −1(0,975) = 1,96. Vậy α ≥ 0,2 . 1,96  α ≥ 0,392

Qui tắc 3: Trong công thức

P(|X − μ | < α) = 2.(α/) − 1 nếu chọn α = 3 thì ta có

P(|X − μ | < 3) = 2.(3) - 1 = 2.0,9987 – 1 = 0,9973

Xác suất này rất gần 1 nên có thể coi sự kiện |X − μ | < 3. là hầu như chắc

chắn.

Vậy ta có qui tắc 3: “Nếu X có phân phối chuẩn N(a,) thì hầu như chắc chắn

X lấy trị số trong khoảng (μ − 3, μ + 3)

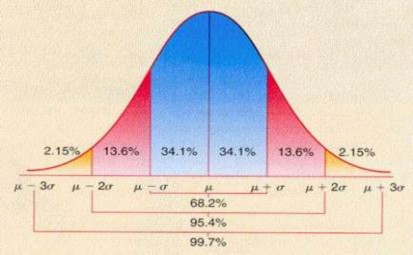
Hình 2.6: Quy tắc 3

Ví dụ 2.26. Trọng lượng của một loại sản phẩm do một nhà máy sản xuất là đại lượng ngẫu nhiên có phân phối chuẩn với kì vọng là 250 gam và phương sai là 25. Sản phẩm được gọi là loại một nếu trọng lượng từ 245 gam đến 260 gam. Tìm tỉ lệ sản phẩm loại một của nhà máy đó.

Giải

Gọi X là trọng lượng của loại sản phẩm đó.

 X  N (250, 25).

Ta cần tìm P(245  X  260).

Theo bài ra, ta có: a = 245, b = 260 ,  = 250,  = 25 = 5. Do đó

P (245  X  260) =

b a  = Φ(2) – Φ(-1)





mà Φ(-1) = 1 - Φ(1)

 P (245  X  260) = Φ(2) + Φ(1) -1

Tra bảng hàm số Laplace, ta được  (1) = 0,8413,  (2) = 0,8772. Vậy, tỉ lệ sản phẩm loại một của nhà máy là

P (245  X  260) = 0,7185.

Ví dụ 2.27. Sản phẩm của một nhà máy được đóng thành từng hộp, mỗi hộp 10 sản phẩm. Gọi X là số sản phẩm loại một có trong hộp. Cho biết X có phân phối xác suất như sau:

7	8	9	10
P	0,2	0,3	0,3	0,2