Các Đặc Trưng Số Của Biến Ngẫu Nhiên

1

a

b

1/b-a

a b

hàm phân phối F(x) hàm mật độ f(x)

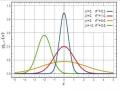
Hình 2.2: Đồ thị hàm phân phối xác suất và hàm mật độ xác suất

Biến ngẫu nhiên X ở trên gọi là tuân theo luật phân phối đều trên [a, b], ký hiệu X ~ U([a,b]).

Ví dụ 2.9. Biến ngẫu nhiên X có hàm mật độ

k.cos x khi

f (x) 

 x 

2 2



a) Tìm k

b) Tìm hàm phân phối F(x).

0 khi x 



 2

c) Tính xác suất P(0 < X < π/4).

Giải:

a) Tìm k.



2

k.cos tdt  1



2

k.2 = 1 k = 1/2

b) Tìm hàm phân phối F(x). Với x[−π/2, π/2] ta có:

x 1 1

F (x) 



2

.cos tdt  (sin x  1) 2 2

Suy ra: hàm phân phối xác suất là:

0





, x 

2

1

2

F (x)  (sin x  1)





1



c) Tính xác suất P(0 < X < π/4).

,

2

,

2

x 

2

x

P(0 < X < π/4) = F(π/4) − F(0) = 1 1 1 1

1

2

2 2

2

2

2.3. Các đặc trưng số của biến ngẫu nhiên

2.3.1. Kỳ vọng

Định nghĩa: Kỳ vọng của biến ngẫu nhiên X, ký hiệu là EX và được xác định như sau:

- Nếu X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất là:

xi

x1	x2	. . .	xi	. . .	xk
pi	p1	p2	. . .	pi	. . .	pk

Có thể bạn quan tâm!

• Lý thuyết xác suất và thống kê toán - 3
• Các Biến Cố A Và A  B Là Xung Khắc.
• Các Phân Phối Xác Suất Của Biến Ngẫu Nhiên
• Lý thuyết xác suất và thống kê toán - 7
• Lý thuyết xác suất và thống kê toán - 8
• Lý thuyết xác suất và thống kê toán - 9

Xem toàn bộ 168 trang tài liệu này.

thì E(X) =

k

xi pi

i1

- Nếu X là biến ngẫu nhiên liên tục có hàm mật độ f(x)



thì EX = x f(x)dx



Tính chất:

(1) E(C) = C (C là hằng số)

(2) E(CX) = C.EX

(3) E(X + Y) = EX + EY

(4) Nếu X và Y là 2 biến ngẫu nhiên độc lập thì E(X.Y) = EX . EY

k

(5) Nếu X là biến ngẫu nhiên rời rạc thì Y = g(X) cũng là biến ngẫu nhiên

rời rạc có kỳ vọng: EY =

g(xi) pi i1

(6) Nếu X là biến ngẫu nhiên liên tục có hàm mật độ f(x) thì Y = g(X) cũng



Ý nghĩa:

là biến ngẫu nhiên liên tục có kỳ vọng: EY =

g(x)f(x)dx



Kỳ vọng của biến ngẫu nhiên là giá trị trung bình mà biến ngẫu nhiên đó nhận, nó phản ánh giá trị trung tâm của phân phối xác suất của biến ngẫu nhiên.

Ví dụ 2.10. Gieo một đồng xu 2 lần. Gọi X = “số lần xuất hiện mặt sấp” . Ta có bảng phân phối xác suất của X là:

xi

0	1	2
pi	1/4	1/2	1/4

EX  0. 1 1. 1  2. 1  1

4 2 4

Ví dụ 2.11. Cho X là biến ngẫu nhiên có hàm mật độ

ìïï

í

f (x)= ïï

3x2

nếu 0 £

x £ 1

Tính EX?

ïï 0 nếu x Ï

îï

[0;1]

Giải

 1 3

EX x f xdx x.3x2dx 

2.3.2. Phương sai

 0 4

Định nghĩa: Phương sai của biến ngẫu nhiên X, ký hiệu là VX và được xác định như sau:

VX = E[(X – EX)2] (2.1)

Ta dễ dàng chứng minh được:

VX = E(X2) – (EX)2 (2.2)

trong đó:



n

i

- Nếu X là biến ngẫu nhiên rời rạc thì E(X2) = x2p

i

i1



- Nếu X là biến ngẫu nhiên liên tục thì E(X2) = x2 f(x)dx



Thật vậy: VX = E[(X – EX)2] = E[(X2 – 2(EX).X + (EX)2]

= E(X2) – 2E[(EX).X] + E[(EX)2]

= EX2 – 2EX.EX + (EX)2

= E(X2) – (EX)2

Tính chất:

Ý nghĩa:

(1) V(C) = 0 , C là hằng số

(2) V(CX) = C2 VX

(3) Nếu X, Y độc lập thì V(X + Y) = VX + VY

Ta thấy (X – EX) là độ lệch khỏi giá trị trung bình EX, nên VX = E[(X – EX)2] là trung bình bình phương độ lệch. Do đó, phương sai của biến ngẫu nhiên là một số không âm dùng để đo mức độ phân tán (mức độ tản mát) của các giá trị của biến ngẫu nhiên X xung quanh tâm EX của nó. VX nhỏ thì mức độ phân tán nhỏ, độ tập trung lớn. VX càng lớn thì độ phân tán càng cao. Trong sản suất kinh doanh, nó đặc trưng cho sự rủi do hay thất bại, sự không ổn định.

Chú ý:

(i) Trong thực hành tính toán phương sai VX, ta nên sử dụng công thức (2.2) để tính.

(ii) Vì đơn vị đo của phương sai bằng bình phương đơn vị đo của đại lượng ngẫu nhiên. Khi cần đánh giá mức độ phân tán các giá trị của đại lượng ngẫu nhiên theo đơn vị của nó, người ta dùng một đặc trưng mới có cùng đơn vị tính với nó – đó là độ lệch tiêu chuẩn.

Căn bậc hai của VX được gọi là độ lệch chuẩn của biến ngẫu nhiên X và được ký hiệu là (X):

(X) = VX

Ví dụ 2.12. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất như sau

X

0	1	2	3	4
P	0,1	0,2	0,3	0,25	0,15

Hãy tính kì vọng, phương sai, độ lệch của X.

Giải:

Kì vọng của X là

E(X) = 0.0,1 + 1.0,2 + 2.0,3 + 3.0,25 + 4.0,15 = 2,15.

Để tính phương sai, ta có hai cách sau.

Cách 1: (Áp dụng công thức (2.1))

V(X) = (0 – 2,15)2.0,1 + (1 – 2,15)2.0,2 + (2 – 21,5)2.0,3 +

(3 – 2,15)2.0,25 + (4 – 2,15)2.0,15 = 1,4275.

Cách 2: (Áp dụng công thức (2.2))

E(X2) = 02.0,1 + 12.0,2 + 22.0,3 + 32.0,25 + 42.0,15 = 6,05 ; V(X) = E(X2) – E2(X) = 6,05 – 2,152 = 1,4275.

Độ lệch chuẩn của X là

(X) = 1,19478.

Ví dụ 2.13. Một xạ thủ có 5 viên đạn, anh ta bắn từng viên một, nếu có 2 viên liên tiếp trúng đích thì dừng bắn. Biết xác suất bắn trúng của mỗi viên là như nhau và bằng 0,9. Gọi X là số viên đạn còn lại.

a) Lập bảng phân phối xác suất của X

b) Tính EX, VX Giải

X = “Số viên đạn còn lại”

a) Bảng phân phối xác xuất của X là:

X

0	1	2	3
P(X)	0.1009	0,0081	0,081	0,81

b) EX  2, 6001; EX2  7, 6221;VX  0,8616 .

Ví dụ 2.14. Cho đại lượng ngẫu nhiên X có hàm mật độ xác suất

,



1 nếu x  (- a , a )

f(x) = 



a2 x2 ,

0

nếu x (- a , a )

Tìm kì vọng, phương sai, độ lệch của X.

Giải:

Kì vọng của X là

a

a2 x2

a xdx 

1 a xdx

aπ a x

a

E(X) = xf (x)dx xodx 

2 2 xodx π 0



Phương sai của X là

a

(vì hàm số lấy tích phân là hàm lẻ)



V(X) = (x 0)2



a

π a2 x2

f (x)dx 

a

x2dx

2 a x2dx

a2 x2

π 

= =

0

Đổi biến số x = asint, ta có



2 2 2 2 a 2 2 a2

= π0

a sin tdt =

0

(1  cos 2t)dt .

2

Độ lệch của X là

a 2

2

 (X) =

Ví dụ 2.15. Cho ĐLNN X có hàm mật độ

ï

ïì a x nếu 0 £

ï

x < 1

f (x)=ïíï

î

ïïï

a) Tìm hằng số a

2 x nếu 1 x  2

0 nếu trái lại

(a là tham số)

Giải

b) Tính



EX ,VX

1 2

a) 



b)

p(x)dx  1 a x dx 2xdx  1

0 1

a  1

EX  1;

EX 2 7 ;VX 1

6 6

2.3.3. Mode

Mode của biến ngẫu nhiên X, ký hiệu ModX, là giá trị tại đó biến X có xác suất lớn nhất (trường hợp rời rạc ) hoặc có mật độ xác suất lớn nhất (trường hợp liên tục).

Như vậy, biến ngẫu nhiên X có thể có nhiều ModX.

Ví dụ 2.16. Cho biến ngẫu nhiên X có bảng phân phối xác suất là:

1	2	3
p(x)	0,6	0,24	0,16

x

Suy ra: ModX = 1

2.3.4. Median (Trung vị)

Trung vị của biến ngẫu nhiên X, ký hiệu MedX, là giá trị m sao cho:

P(X < m) = P( X  m) = 0,5

Trung vị thực chất là giá trị của biến ngẫu nhiên X chia phân phối thành 2 phần có xác suất bằng nhau. Trong nhiều trường hợp ứng dụng, trung vị là đặc trưng vị trí rất tốt, nhiều khi tốt hơn cả kỳ vọng, nhất là khi trong số liệu có những sai sót thái quá.

Nếu X là biến ngẫu nhiên liên tục thì m là trung vị khi

m

f(x)dx  0.5 hay F(m) = 0.5.



Còn nếu X là biến ngẫu nhiên rời rạc thì giá trị trung vị chỉ được xác định một cách tương đối, bởi vì nhiều khi không tồn tại giá trị m để F(m) bằng đúng 0,5. Vì vậy, thông thường người ta xác định giá trung vị của biến ngẫu nhiên rời rạc X là giá trị xi nếu thỏa mãn điều kiện:

F(xi)  0,5 < F(xi+1)

Ví dụ 2.17. Cho X là biến ngẫu nhiên có hàm mật độ là:

ìïï

ïï

f (x)= ï

0 nếu

x3

x < 0

ï

ïí x 4

ï

nếu 0 x  2

Tìm Median của X ? Giải

ïïî

0 nếu

x > 2

Međian cần tìm từ điều kiện

P X m1 .

2

Ta có

m



P X mx 

x3 m2

4 dx 2

m4

4  8

16

Suy ra

0 

m m  1 4 2

2 4

m  8m  8  0 m 

4  8

4  8

2 16 2

. Trong 4 nghiệm này ta

phải chọn sao cho

m 0; 2do đó m 

. Vậy

MedX .

2.4. Các phân phối xác suất thường dùng

2.4.1. Phân phối nhị thức

a. Bài toán

Xét một dãy n phép thử độc lập giống nhau, trong mỗi phép thử chỉ có 2 kết cục

hoặc xảy ra A hoặc không xảy ra A, và P(A) = p , P( A ) = 1 - p = q không phụ thuộc vào số thứ tự của mỗi phép thử.

n

Xác suất để trong dãy n phép thử độc lập nói trên, sự kiện A xuất hiện đúng k lần, ký hiệu Pk và được xác định bởi công thức:

Pk =

C k pk q nk

(2.3)

Công thức (2.3) được gọi là công thức Becnulli

Gọi X là “Số lần xuất hiện biến cố A trong n phép thử độc lập” nói trên. Ta thấy X là biến ngẫu nhiên rời rạc với miền giá trị là: 0,1, 2,..., n

n

Theo công thức Bernoulli: P X k= Pk = C k pk q nk

(2.4)

b. Định nghĩa

Biến ngẫu nhiên rời rạc X được gọi là có phân phối nhị thức với tham số n, p và ký hiệu là X ~ B(n , p) (trong đó n N và 0 p 1) nếu X nhận một trong các giá trị có thể có X = {0 , 1 , 2 , . . . , n} với xác suất tương ứng được tính bằng công thức (2.4).

Ví dụ 2.18. Xác suất thành công của một thí nghiệm là 40%. Một nhóm gồm 9 sinh viên tiến hành thí nghiệm đó một cách độc lập. Tính xác suất để:

a) Có đúng 6 thí nghiệm thành công,

b) Có ít nhất 1 thí nghiệm thành công,

c) Có ít nhất 8 thí nghiệm thành công.

Giải

Gọi X = “số thí nghiệm thành công“

X có phân phối nhị thức với tham số n = 9, p = 0.4

9

a) P X 6C6 0, 46.0, 64  0, 04459

9

b) P X 1 1P X 0 1C0 0, 400, 69  0,9899

9 9

c) P X 8P X 8P X 9C80, 480, 61 C9 0, 490, 60  0, 0038

c. Định lý. Nếu X ~ B(n , p) thì

(1) EX = np

(2) VX = npq

(3) modX = [(n + 1)p] ([a] chỉ phần nguyên của a)

Ví dụ 2.19. Một xạ thủ bắn 40 viên đạn. Biết xác suất bắn trúng mục tiêu của mỗi viên đạn đều là 0,7. Tính kì vọng, phương sai, độ lệch của số viên đạn trúng mục tiêu.

Giải:

Ta có X  B (40 ; 0,7), tức là X có phân phối nhị thức với n = 40, p = 0,7. Do đó E (X) = np = 40 . 0,7 = 28

V(X) = np (1-p) = 40 . 0,7 . 0,3 = 8,4

 (X) = 2,898.

Ví dụ 2.20. Tỉ lệ cử tri ủng hộ ứng cử viên A trong một cuộc bầu cử tổng thống là 60%. Người ta hỏi ý kiến 20 cử tri được chọn một cách ngẫu nhiên. Gọi X là số người bỏ phiếu cho ông A trong 20 người đó.

a) Tìm giá trị trung bình, độ lệch chuẩn của X và mod của X,

b) Tìm P X  1.

Giải:

Dễ thấy X có phân phối nhị thức với tham số n =20; p =0,6; q = 0,4

20 20

Suy ra: EX = np = 12; VX = npq = 4,8; σX ≈ 2,19; modX = [12,6] = 12 P{X ≤ 1} = Co (0,6)o(0,4)20 + C1 (0,6)(0,4)19  3.408.107

2.4.2. Phân phối Poisson

a. Định nghĩa

Biến ngẫu nhiên rời rạc X có phân phối Poisson vói tham số , ký hiệu X ~ P(), nếu X nhận một trong các giá trị có thể có X = 0 , 1 , 2 , . . . với các xác suất tương ứng được tính bằng công thức:

P{X = k} =

k

e

k!

Chú ý: mối quan hệ giữa phân phối nhị thức và phân phối Poisson

Cho X  B (n, p). Nếu p khá bé và n khá lớn có thể xem X  P (np). Khi đó

P(X = k) =

Ck pk

1 p

n

nk

enp (np)k



k! .

Ví dụ 2.21. Một gara cho thuê ô tô thấy rằng số người đến thuê ô tô vào ngày thứ 7 là một ĐLNN X có phân phối Poát xông với tham số  = 2. Giả sử ga ra có 4 chiếc ô tô. Hãy tìm xác suất để:

a) Không phải tất cả 4 chiếc đều được thuê,

b) Tất cả 4 ô tô đều được thuê,

c) Gara không đáp ứng được yêu cầu.

Giải:

d) Gara cần có ít nhất bao nhiêu ô tô để xác suất không đáp ứng được nhu cầu thuê xe bé hơn 2%.

a) P{Không phải tất cả 4 chiếc đều được thêu} = P{X ≤ 3} = 0,857

b) P{Tất cả 4 ô tô đều được thuê} = P{X  4} = 1 – P{X ≤ 3}

= 1 – 0,857 = 0,143

c) P{Gara không đáp ứng được yêu cầu} = P{X > 4}

= 1 – P{X ≤ 4} = 1 – 0,947 = 0,053