Lý thuyết xác suất và thống kê toán - 8

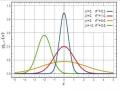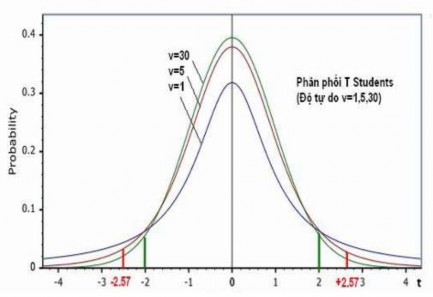
Hình 2.7: Phân phối Student

Chú ý:



n

X

2

i

i1

n

Nếu X, X1, X2, ... Xn độc lập cùng phân phối N(0, 1) thì: X

có phân phối

Student với bậc tự do n.

2.4.6. Phân phối Fisher – Sendecor

a. Bài toán

Trong các phân tích dữ liệu, đặc biệt trong kinh tế lượng ta thường gặp những

thông báo, tính toán dạng

F (n1, n2). Vậy F ký hiệu cho biến ngẫu nhiên nào?

1 1 2 2

Cho Z : c 2 (n ); Z : c 2 (n ). Xét biến ngẫu nhiên F =

Z1 / n1 Z2 / n2

Đây là biến ngẫu nhiên liên tục xác định trên (- ¥

;+ ¥

). Phân phối của F

gọi là phân phối Fisher – Snedecor với

n1, n2

bậc tự do. Ký hiệu là

F (n1, n2 )

b. Định nghĩa: Phân phối Fisher – Snedecor với

n1, n2

bậc tự do là phân phối của biến

ngẫu nhiên liên tục

F (n1, n2) trên (- ¥

;+ ¥

) với hàm mật độ

ï

ïì0

ï

ï n1 + n2

ï

với

x £ 0

f (x)= íïï C.

x 2

n1+ n2

với

x > 0

2

ïï (n + n x)

trong đó

îï 2 1

æn + n ö n1n2

Gçç 1 2 ÷n1 2 n2 2

C = çè

2

æçn1ö÷

÷ø.

æçn2ö÷

Gç ÷Gç ÷

è 2 ø è 2 ø

c. Định lý. Nếu F là biến ngẫu nhiên có phân phối Fisher – Snedecor với do thì :

n1, n2

bậc tự

(1) E(F )=

n1

n2 - 2

2 1 2

(2) V (F )=

2n2 (n + n2 + 2)

n (n - 2)2 (n - 4)

1 2 2

HƯỚNG DẪN TỰ HỌC CHƯƠNG 2

Trong khi giải các bài toán của chương 2, sinh viên cần nắm được các khái niệm, tính chất và ý nghĩa thực tiễn của các khái niệm.

1. Để nắm được khái niệm biến ngẫu nhiên, cần trả lời được các câu hỏi sau: Thế nào là biến ngẫu nhiên?

Sự khác biệt giữa biến ngẫu nhiên và biến chắc chắn?

2. Biến ngẫu nhiên được phân thành 2 loại chính là: biến ngẫu nhiên rời rạc và biến ngẫu nhiên liên tục.

a) Để mô tả biến ngẫu nhiên rời rạc, ta dùng khái niệm bảng phân phối xác suất, đó là bảng với hai thông tin: các giá trị mà biến ngẫu nhiên nhận và xác suất của biến ngẫu nhiên tương ứng với các giá trị đó.

x

x1	x2	. . .	xi	. . .	xn
p(x)	p1	p2	. . .	pi	. . .	pn

Có thể bạn quan tâm!

• Các Phân Phối Xác Suất Của Biến Ngẫu Nhiên
• Các Đặc Trưng Số Của Biến Ngẫu Nhiên
• Lý thuyết xác suất và thống kê toán - 7
• Lý thuyết xác suất và thống kê toán - 9
• Lý thuyết xác suất và thống kê toán - 10
• Các Tính Chất Của Ước Lượng Điểm

Xem toàn bộ 168 trang tài liệu này.

Trong đó:

n

pi P X xi ; pi  1.

i1

Như vậy, bài toán đầu tiên gặp trong chương này là: Lập bảng phân phối xác suất của biến ngẫu nhiên rời rạc. Để lập được bảng phân phối xác suất cần:

- Chỉ ra được các giá trị mà biến ngẫu nhiên nhận

- Tính được xác suất tương ứng với các giá trị đó.

b) Để mô tả biến ngẫu nhiên liên tục, ta dùng khái niệm hàm mật độ. Hàm

gọi là hàm mật độ của biến ngẫu nhiên X nếu nó thỏa mãn 2 điều kiện sau:

p xđược

i) p x 0, x  ¡



ii) 



p xdx  1

Câu hỏi đặt ra đó là: Tại sao không dùng được bảng phân phối xác suất để mô tả biến ngẫu nhiên liên tục?

Bài toán đặt ra là:

- Cho hàm

p x, xác định điều kiện để

p x

là hàm mật độ của biến ngẫu

nhiên X trên một miền nào đó.

- Cho

p x

là hàm mật độ của biến ngẫu nhiên X,

p x

phụ thuộc tham số k

nào đó, xác định k ?

3. Hàm phân phối xác suất

Hàm phân phối xác suất của biến ngẫu nhiên X, ký hiệu F(x), là xác suất để

biến ngẫu nhiên X nhận giá trị nhỏ hơn x, với x là một số thực bất kỳ.

F(x) = P(X < x)

Như vậy, cho giá trị thực x , giá trị của hàm F tại x là xác suất để biến ngẫu nhiên X nhận giá trị bên trái điểm x .

Miền xác định của hàm F là x  ¡

Miền giá trị của F là : 0;1

Tính chất: F(x) là hàm không giảm, tức là nếu x1 < x2 thì F(x1) ≤ F(x2)

Khái niệm hàm phân phối xác suất được dùng cho cả 2 biến ngẫu nhiên rời rạc và liên tục với công thức xác định là:

- Nếu X là đại lượng ngẫu nhiên rời rạc có bảng phân phối xác suất:

X

x1	x2 …	xn
P	p1	p2 …	pn

Với x1 < x2 < … < xn, thì hàm phân phối xác suất của X là

0



p1

,neáu

,neáu

x  x1 x  x  x2

F(x) =

pi =

........................... .............

...............

xi x

p  p  ....  p ,neuá x

 x  x

1 2 n 1

 1

,neáu

n 1 n

x  xn

- Nếu X là biến ngẫu nhiên liên tục có hàm mật độ

p xthì:

Chú ý:

F 'xp x

x

F x



p t dt

4. Các đặc trưng số của biến ngẫu nhiên

- Kỳ vọng của biến ngẫu nhiên chính là giá trị trung bình mà biến ngẫu nhiên nhận, nó được dùng hàng ngày trong mọi lĩnh vực của khoa học và đời sống, chẳng hạn như năng suất lúa trung bình, nhiệt độ trung bình, mức tiêu thụ điện năng trung bình,…

- Một đặc trưng khác của biến ngẫu nhiên là phương sai VX hay bình phương

độ lệch 2 . Phương sai càng nhỏ thì các giá trị của biến ngẫu nhiên càng tập trung

VX

xung quanh giá trị trung bình của nó, còn nếu phương sai càng lớn thì các giá trị của

biến ngẫu nhiên càng phân tán. Thay cho việc dùng 2 , ta dùng độ lệch chuẩn.

được gọi là

- Ngoài ra, ta còn dùng các đặc trưng như ModX, MedX của biến ngẫu nhiên X.

- Các đặc trưng của biến ngẫu nhiên được xác định thông qua tính tổng của các

số hạng nào đó (đối với biến ngẫu nhiên rời rạc) hoặc tính tích phân (đối với biến ngẫu nhiên liên tục) vì vậy để học tốt phần này, sinh viên cần ôn tập tính tích phân xác định.

5. Các phân phối xác suất thường dùng

- Phân phối nhị thức: thường gặp trong dãy thử Bernoulli. Trong các bài toán phân phối nhị thức thông thường đòi hỏi ta phải nhận được dãy thử

Bernoulli.

- Phân phối Poisson: thường gặp trong các bài toán đếm sự xuất hiện của một biến cố nào đó.

- Phân phối chuẩn: thường gặp trong các bài toán sai số khi đo đạc các đại lượng trong vật lý, thiên văn,… Trong thực tế, nhiều biến ngẫu nhiên tuân theo quy luật chuẩn chẳng hạn như: trọng lượng, chiều cao, năng suất, mức lãi hay mức tiêu thụ một mặt hàng nào đó,…

- Với mỗi phân phối xác suất, ta khảo sát bảng phân bố xác suất hoặc hàm mật độ của nó, các tính chất và các đặc trưng của nó. Để tìm hiểu sâu hơn các phân phối xác suất thường dùng, sinh viên có thể đọc thêm trong các tài liệu tham khảo [1],[3],[5].

CÂU HỎI ÔN TẬP CHƯƠNG 2

2.1. Biến ngẫu nhiên luôn nhận giá trị dương.

a) Đúng b) Sai

2.2. Biến ngẫu nhiên rời rạc chỉ nhận một số hữu hạn giá trị

a) Đúng b) Sai

2.3. Kỳ vọng của biến ngẫu nhiên rời rạc là giá trị nó lấy thường xuyên nhất.

a) Đúng b) Sai

2.4. Kỳ vọng của tổng hai biến ngẫu nhiên luôn bằng tổng kỳ vọng của hai biến ngẫu nhiên đó.

a) Đúng b) Sai

2.5. Hai biến ngẫu nhiên có cùng kỳ vọng sẽ có cùng phương sai.

a) Đúng b) Sai

2.6. Biến ngẫu nhiên tồn tại phương sai thì cũng tồn tại kỳ vọng và ngược lại.

a) Đúng b) Sai

2.7. Hàm mật độ

p xcủa biến ngẫu nhiên liên tục luôn dương.

a) Đúng b) Sai

2.8. Tổng của hai biến ngẫu nhiên có phân phối nhị thức là biến ngẫu nhiên có phân phối nhị thức.

a) Đúng b) Sai

2.9. Biến ngẫu nhiên có phân phối Poisson là biến ngẫu nhiên rời rạc.

a) Đúng b) Sai

2.10. Nếu X có phân phối chuẩn

N ;2 

thìX 



có phân phối chuẩn tắc.

a) Đúng b) Sai

BÀI TẬP CHƯƠNG 2

2.1. Cho đại lượng ngẫu nhiên X có bảng phân phối xác suất sau đây :

X

0	1	2	3	4	5	6	7
P	0	a	2a	2a	3a	a2	2a2	7a2 + a

a) Tính a,

b) Tính P(X  5), P(X < 3).

2.2. Trong một hộp có 10 sản phẩm, trong đó có 4 phế phẩm. Lấy ngẫu nhiên lần lượt ra 4 sản phẩm. Gọi X là số sản phẩm tốt lấy ra.

a) Hãy lập bảng phân phối xác suất ,

b) Tính EX, VX?

2.3. Một hộp có 5 viên bi: 3 trắng, 2 đỏ. Lấy ngẫu nhiên ra 2 viên bi. Gọi X là số bi đỏ được lấy ra.

a) Lập bảng phân phối xác suất của X,

b) Tìm hàm phân phối

c) Tính EX, VX.

F x,

2.4. Một xạ thủ có 5 viên đạn, anh ta bắn từng viên với xác suất bắn trúng của

các viên là 0,9. Anh ta bắn theo nguyên tắc nếu có 2 viên liên tiếp bắn trúng bia thì dừng lại, gọi X là số viên đạn còn lại.

a) Lập bảng phân phối xác suất của X,

b) Tìm hàm phân phối

c) Tính EX, VX.

F x,

2.5. Cho ĐLNN liên tục X có hàm mật độ:

ï

ïì k x21

ï

nếu

x Î [2;3]

ï

f (x)= ïí

ï

ï î

0 nếu

x Ï [2;3]

a) Tìm hằng số k,

b) Tính EX , VX.

2.6. Cho ĐLNN X có hàm mật độ:

ìïï

í

f (x)=ïï

kx2x 22

nếu

x Î [0; 2]

ï

ïï 0 nếu

îï

x Ï [0; 2]

a) Xác định hằng số k,

b) Tìm hàm phân phối

F x.

2.7. Tuổi thọ của một loại côn trùng nào đó là một ĐLNN X ( tính bằng tháng) với hàm mật độ:

kx 2 (4  x) f (x) 

0

khi khi

x [0,4]

x [0,4]

a) Xác định k ,

b) Tính EX , VX,

c) Tìm xác suất để côn trùng chết trước 1 tháng tuổi.

2.8. Cho ĐLNN X có hàm mật độ:

ï

ïì ax nếu 0 £

ï

x < 1

f (x)= ïí

a 3 x

nếu 1£

x < 3

ï

ï

ï îï 0 nếu trái lại

a) Xác định hằng số a,

b) Tìm kỳ vọng và phương sai của X.

2.9. Cho ĐLNN X có hàm mật độ:

ï

ïì a x  2

ï

nếu - 2 £

x < 0

f (x)= ïí

a 1x2 

nếu 0 £

x < 1

ï

ï

ï îï 0 nếu trái lại

a) Tìm hằng số k,

b) Tìm hàm phân phối F(x),

c) Tìm kỳ vọng, phương sai .

2.10. Cho ĐLNN X có hàm mật độ:

ï

ïì ax nếu 0 £

ï

x < 1

f (x)= ïí

2 x

nếu 1£

x < 2

ï

ïï 0 nếu trái lại

îï

a) Tìm hằng số a,

b) Tìm kỳ vọng, phương sai .

2.11. Cho ĐLNN X có hàm mật độ