1. Hoạt Động Tự Học Của Học Sinh Trước Khi Đến Lớp

Phụ lục 7

PHIẾU KHẢO SÁT Ý KIẾN HIỆU QUẢ CỦA VIỆC SỬ DỤNG ĐTDĐ HỖ TRỢ HỌC SINH TỰ HỌC MÔN TOÁN

Phụ lục 8

GIÁO ÁN THỰC NGHIỆM SƯ PHẠM

Bài 1: Tính đơn điệu của hàm số (tiết 1)

I. Mục tiêu bài học:

Kiến thức: Hiểu định nghĩa đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái niệm này với đạo hàm. Nắm được qui tắc xét tính đơn điệu của hàm số. Tư duy các vấn đề toán học một cách lôgic và hệ thống.

Kĩ năng: Biết vận dụng qui tắc xét tính đơn điệu của một hàm số và dấu đạo hàm của nó.

Thái độ: Có động cơ và tích cực tham gia các HĐ tự học; Rèn luyện tính cẩn thận, chính xác.

II. Chuẩn bị trước giờ lên lớp

Giáo viên: Giáo án. Hình vẽ minh hoạ.

Học sinh: SGK, SBT và hoàn thành nhiệm vụ tự học được giao.

III. Hoạt động dạy học

III.1. Hoạt động tự học của học sinh trước khi đến lớp

Nhiệm vụ 1. Truy cập trang web mlearningvn.com đọc lại và làm các ví dụ của các phần kiến thức sau: Định nghĩa hàm số nghịch biến, hàm số đồng biến; Các quy tắc tính đạo hàm; Cách xét dấu của các hàm số.

Nhiệm vụ 2; Giả sử hàm số y = f(x) xác định trên K. Hãy thực hiện việc ghép đôi và phát biểu khái niệm hàm số đồng biến, hàm số nghịch biến.

1) y = f(x) đồng biến trên K

2) y = f(x) nghịch biến trên K

a).x1, x2 K: x1 < x2 f(x1) > f(x2)

b).x1, x2 K: x1 < x2 f(x1) < f(x2)

Có thể bạn quan tâm!

Xem toàn bộ 221 trang tài liệu này.

Kết quả: (1) ↔ (b); (2) ↔ (a).

Nhiệm vụ 3: Hãy chỉ ra các điều kiện tương đương

1)f (x1) f (x2 ) 0 , x1,x2K (x1 x2)

x1 x2

2).f (x1) f (x2 ) 0 , x1,x2K (x1 x2)

x1 x2

a).x1, x2 K: x1 < x2 f(x1) < f(x2) b).x1, x2 K: x1 < x2 f(x1) > f(x2)

Kết quả: (1) ↔(a) và (2) ↔(b).

III.2. Các hoạt động trong giờ lên lớp

1x2

Hoạt động 1: Tính đạo hàm, lập bảng xét dấu các đạo hàm đó (10’). GV phân chia lớp thành 4 nhóm với các nhiệm vụ cụ thể sau:

1 x2

0 1

f’(x)

0 -

Nhóm 1:

f (x) 

trên đoạn [0; 1]

ĐS:

f '(x) x

Nhóm 2:

f (x) x 4 trên TXĐ

ĐS f '(x) 

x2  4

-

-2

2 +

f’(x)

0 +



Nhóm 3: f xx 1

2x 1

trên TXĐ

ĐS:

f 'x 1

2x 12

-1 +

f(x)

+ 0 +

GV chốt lại đáp án cho các nhóm.

HS có thể sử dụng ĐTDĐ tại lớp để tra cứu bảng liệt kê công thức tính đạo hàm của một số hàm số và cách lập bảng xét dấu hàm số trên mlearningvn.com.

Hoạt động 2: Tìm hiểu mối liên hệ giữa tính đơn điệu của hàm số và dấu của đạo hàm (5’)

GV nêu vấn đề: Kết quả hoạt động nhóm cho ta thấy 3 trường hợp: Đạo hàm của hàm số không đổi dấu trên miền xác định (nhóm 1); đổi dấu (nhóm 2) trên miền

xác định và không đổi dấu trên miền xác định trừ một vài điểm (nhóm 3). Hãy nghiên cứu, đưa ra dự đoán về mối liên hệ giữa dấu của đạo hàm bậc nhất với tính đơn điệu của hàm số. GV chính xác hóa ý kiến HS và đưa ra định lý:

Định lí: Cho hàm số y = f(x) có đạo hàm trên khoảng I. Nếu f '(x) > 0, x I thì y = f(x) đồng biến trên I.

Nếu f '(x) < 0, x I thì y = f(x) nghịch biến trên I. Nếu f (x) = 0, x I thì f(x) không đổi trên K.

Chú ý: Nếu f liên tục trên [a; b] và có đạo hàm f’(x) > 0 trên (a; b) thì hàm số f đồng biến trên [a; b].

Hoạt động 4: Áp dụng xét tính đơn điệu của hàm số (5’)

GV yêu cầu các nhóm dựa vào bảng xét dấu của nhóm mình và định lý vừa học chỉ ra các khoảng đồng biến nghịch biến của hàm số. Kết quả:

Nhóm 1: Hàm số nghịch biến trên đoạn [0; 1]

Nhóm 2: Hàm số đồng biến trên mỗi khoảng (-; -2) và (2; +), nghich biến trên mỗi khoảng (-2; 0) và (0; 2)

Nhóm 3: Hàm số đã cho đồng biến trên mỗi nửa khoảng (-;

Hoạt động 5: Bài tập tại lớp (15’)

1 1

) và (

2 2

; +)

5.1. GV yêu cầu HS đưa ra các bước để xét tính đơn điệu của hàm số, sau đó chính xác hóa:

- Bước 1: Tính đạo hàm bậc nhất;

- Bước 2: Tìm x0 thuộc TXĐ làm cho y’ = 0 hoặc y’ không xác định.

- Bước 3: Lập bảng biến thiên

5.2. Giải bài tập:

Bài tập 1: Tìm khoảng đơn điệu của hàm số: y 

x x  3,x  0;

Lời giải: y ' 3 x x 1; y’ = 0  x = 1; y’ không xác định khi x = 0

Bảng biến thiên

0 1 +

y’

- 0 +

0 +

-2

Kết luận: Hàm số nghịch biến trên (0; 1) và đồng biến trên khoảng (1; +)

Bài tập 2: Tìm các giá trị của tham số a để hàm số biến trên R.

Lời giải:

Ta có f’(x) = x2 + 2ax + 4, ’ = a2 – 4.

f (x) 1 x3  ax2  4x  3 đồng

- Nếu a2 – 4 < 0 hay -2 <a < 2 thì f’(x) > 0 xR Hàm số đồng biến trên R.

- Nếu a = 2 thì f’(x) = (x+ 2)2 > 0 với mọi x ≠ -2. Hàm số đồng biến trên R. Tương tự nếu a = -2 thì hàm số đồng biến trên R.

- Nếu a < -2 hoặc a >2 thì f’(x) = 0 có 2 nghiệm phân biệt x1 và x2. Giả sử x1 < x2. Khi đó hàm số nghịch biến trên khoảng (x1; x2). Các giá trị này của a không thỏa mãn điều kiện đòi hỏi.

Kết luận: Hàm số đồng biến trên R  -2  a  2

GV yêu cầu HS đưa ra nhận xét trong trường hợp f có đạo hàm trên K. Nếu f’(x)  0 xK (hoặc f’(x)  0 xK) và f’(x) = 0 chỉ tại một số hữu hạn điểm của K, sau đó GV chính xác hóa, phát biểu định lý.

Định lý: Giả sử hàm số f có đạo hàm trên K. Nếu f’(x)  0 xK (hoặc f’(x) 0

xK) và f’(x) = 0 chỉ tại một số hữu hạn điểm của K thì hàm số f đồng biến (hoặc nghich biến) trên K

Hoạt động 6: Củng cố, giao nhiệm vụ về nhà (4’)

- Truy cập hệ thống mlearningvn.com và hoàn thành các câu hỏi trắc nghiệm, giải các bài tập được gợi ý

Nhận xét: Việc sử dụng một số ứng dụng của ĐTDĐ hỗ trợ HS tự học toán không chỉ diễn ra trước và sau giờ giảng mà tại một số thời điểm GV có thể cho phép HS sử dụng chức năng sổ tay toán học trên ĐTDĐ cũng như sử dụng các chức năng tính toán được cài đặt trên ĐTDĐ.

I. MỤC TIÊU:

Kiến thức:

Phụ lục 9

GIÁO ÁN THỰC NGHIỆM SƯ PHẠM Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG

- Nắm được vectơ pháp tuyến, cặp vectơ chỉ phương của mặt phẳng.

- Nắm được sự xác định mặt phẳng. Phương trình tổng quát của mặt phẳng.

- Điều kiện để hai mặt phẳng song song, vuông góc.

Kĩ năng:

- Biết cách lập phương trình tổng quát của mặt phẳng khi biết một điểm và vectơ pháp tuyến.

- Xác định được hai mặt phẳng song song, vuông góc.

- Tính được khoảng cách từ một điểm đến mặt phẳng.

Thái độ:

- Liên hệ được với nhiều vấn đề trong thực tế với bài học.

- Phát huy tính độc lập, sáng tạo trong học tập.

II. CHUẨN BỊ:

Giáo viên: Giáo án. Hình vẽ minh hoạ.

Học sinh: SGK, SBT và thực hoàn thành nhiệm vụ tự học được giao.

III. Hoạt động dạy học

III.1. Hoạt động tự học của học sinh trước khi đến lớp

Nhiệm vụ 1. Truy cập trang web mlearningvn.com đọc lại và làm các ví dụ của các phần kiến thức sau: khái niệm, các tính chất và ứng dụng của tích có hướng của 2 véc tơ;

Nhiệm vụ 2. Truy cập trang web mlearningvn.com tự đọc và làm các ví dụ của các phần kiến thức sau: phương trình mặt phẳng và các trường hợp riêng;

Nhiệm vụ 3: Tìm VTPT tương ứng của các mặt phẳng sau và ghép với kết quả:

(1) Qua A(2; –1; 3), B(4; 0; 1), C(–10; 5; 3).

(2) Qua A(2; 0; 0), B(0; 2; 0), C(0; 0; 2).

(3) Mặt phẳng (Oxy).

(4) Mặt phẳng (Oyz).

(a) n 1;1;1

(b) n 0;0;1

(d) n 1;0;0

Kết quả: (1) ↔ (c); (2) ↔ (a); (3) ↔ (b); (4) ↔ (d)

Nhiệm vụ 4: Xác định một VTPT của các mặt phẳng: a) 4x  2y  6z  7  0

b) 2x  3y  5  0

Đáp số: a) n  (4;2;6) b) n  (2;3;0)

III.2. Các hoạt động trong giờ lên lớp

Hoạt động 1: Tìm hiểu phương trình tổng quát của mặt phẳng

Bài toán 1: Trong không gian Oxyz, cho mp (P) đi qua

M0 (x0 ; y0 ; z0 )

và nhận

n  ( A; B;C) làm VTPT. Điều kiện cần và đủ để M(x; y; z)  (P) là:

M0M n

A(x x0 ) B(y y0 ) C(z z0 )  0 (?1) Nêu điều kiện để M  (P)? M  (P) 

Bài toán 2: Trong KG Oxyz, tập hợp các điểm M(x; y; z) thoả PT: Ax By Cz D  0 (A, B, C không đồng thời bằng 0) là một mặt phẳng nhận vectơ n  ( A; B;C) làm VTPT.

(?2). Chỉ ra một VTPT của (P)?

n  ( A; B;C)

Định nghĩa: Phương trình

Ax By Cz D  0, trong đó

A2 B2 C2  0,

được gọi là phương trình tổng quát của mặt phẳng.

Nhận xét:

a) (P): Ax By Cz D  0 (P) có 1 VTPT là n  ( A; B;C) .

b) PT của (P) qua M0 (x0 ; y0 ; z0 ) và có VTPT n  ( A; B;C) là:

A(x x0 ) B(y y0 ) C(z z0 )  0

Hoạt động 2: Tìm hiểu các trường hợp riêng của phương trình tổng quát của mặt phẳng

(?1). Khi (P) đi qua O, tìm D? D = 0

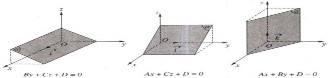
(?2) Phát biểu nhận xét khi một trong các hệ số A, B, C bằng 0?

Hệ số của biến nào bằng 0 thì (P) song song hoặc chứa trục ứng với biến đó.

(?3) Tìm giao điểm của (P) với các trục toạ độ?

(P) cắt các trục Ox, Oy, Oz lần lượt tại A(a; 0; 0), B(0; b; 0), C(0; 0; c).

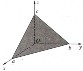
2. Các trường hợp riêng

a) D = 0 (P) đi qua O.

(P) Ox

(P) (Oxy)



b) A = 0 (P)

c) A = B = 0 



(P)  (Oxy)

Nhận xét: Nếu các hệ số A, B, C, D đều khác 0 thì có thể đưa phương trình của (P)

về dạng:

x y z  1

a b c

(2)

(2) được gọi là phương trình của mặt phẳng theo đoạn chắn.

Hoạt động 3: Áp dụng phương trình mặt phẳng VD1: Lập phương trình của mặt phẳng đi qua các điểm: a) A(1; 1; 1), B(4; 3; 2), C(5; 2; 1)

b) A(1; 0; 0), B(0; 2; 0), C(0; 0; 3)

(?) Xác định một VTPT của mặt phẳng? a) n AB, AC (1;4;5)

 (P): x  4 y  5z  2  0