9. Dùng giải thuật Midpoint viết hàm sinh đường tròn có toạ độ tâm (xc, yc) và bán kính r.
10. Áp dụng các giải thuật DDA, Bresenham, Midpoint tính các điểm được vẽ trên các đoạn thẳng giới hạn bởi các cặp điểm sau:
a. A(9, 22), B(19, 28)
b. C(10,10), D(15, 21)
c. E(9, 19), F(1, 29)
11. Tính các điểm được vẽ trên các đường tròn sau:
a. Đường tròn có phương trình (x – 2)2 + (y-7)2 = 121 theo thuật toán Midpoint
b. Đường tròn có bán kính bằng 13 và tâm tại điểm (1, -5) theo thuật toán Bresenham
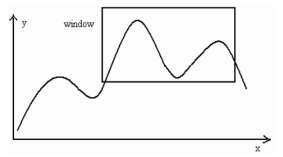
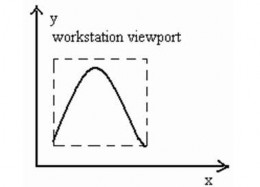
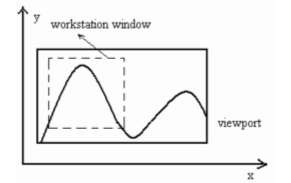
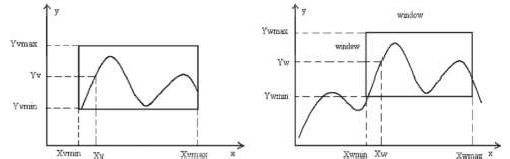
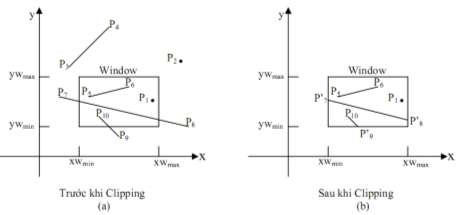
12. Cài đặt thủ tục vẽ đoạn thẳng theo thuật toán Bresenham và MidPoint cho các trường hợp hệ số góc m>1, m<-1, -1 13. Viết thủ tục LineTo(x,y:Integer); để vẽ đoạn thẳng từ vị trí hiện thời đến điểm có tọa độ (x,y). 14. Viết thủ tục LineRel(dx,dy:Integer); để vẽ đoạn thẳng từ vị trí hiện thời đến điểm mới cách điểm hiện thời một khoảng theo trục x là dx và theo trục y là dy. 15. Cài đặt thủ tục vẽ đường tròn theo thuật toán MidPoint. 16. Viết thủ tục Arc(x0,y0,g1,g2:Integer; R:Word); để vẽ cung tròn có tâm (x0,y0) bán kính R với góc bắt đầu là g1 và góc kết thúc là g2. 17. Viết thủ tục Sector(x0,y0,g1,g2:Integer; Rx,Ry:Word); để vẽ cung Ellipse có tâm (x0,y0) bán kính theo trục X là Rx, bán kính theo trục Y là Ry với góc bắt đầu là g1 và góc kết thúc là g2. 18. Viết thủ tục DrawPoly(P:Array; n:Byte; xc,yc,R:Word); để vẽ một đa giác đều có n đỉnh lưu trong mảng P nội tiếp trong đường tròn tâm (xc,yc) bán kính R. 19. Viết thủ tục Circle3P(A,B,C:ToaDo2D); để vẽ đường tròn đi qua 3 điểm A,B,C. 20. Viết thủ tục Arc3P(A,B,C:ToaDo2D); để vẽ cung tròn đi qua 3 điểm A,B,C. 21. Vẽ đồ thị các hàm số sau: y = ax2 + bx + c, y = ax3 + bx2 + cx + d, y = ax4 + bx3 + cx2 + dx + e y = ax b , y = cx d ax 2 bx c . dx e 22. Vẽ các đường cong sau: 2 y2 = 2pxx a 2 + y 2 = 1 b 2 x - y 2 2 a 2 b 2 = 1 Hướng dẫn giải bài tập 1. a. Stt 1 2 3 4 5 6 7 8 9 x 10 11 12 13 14 15 16 17 18 y 20 21 22 23 24 24 25 26 27 Có thể bạn quan tâm! Xem toàn bộ 240 trang tài liệu này. b. Stt 1 2 3 4 5 6 7 8 9 x 16 17 18 19 20 21 22 23 24 y 19 20 21 21 22 23 24 24 25 P 4 0 -4 8 4 0 -4 8 4 c. Stt 1 2 3 4 5 6 7 8 9 x 15 16 17 18 19 20 21 22 23 y 17 18 18 19 19 20 21 21 22 P 2 -4 6 0 10 4 -2 8 2 2. a. Stt 1 2 3 4 5 6 7 8 9 x 6 7 8 9 10 11 12 13 14 y 14 14 14 14 13 13 12 11 11 P -10 -7 -2 5 -6 5 0 -1 16 b. Stt 1 2 3 4 5 6 7 8 9 x 5 6 7 8 9 10 11 12 13 y 15 15 15 15 14 14 13 12 11 P -17 -11 -1 13 -5 17 11 13 23 3. - Giải thuật DDA sinh đường thẳng với hệ số góc m > 1, Dx >0. void ddaline (int x1,int y1,int x2,int y2,int c) { int x=x1; float y=y1; float k=(float)(x2-x1)/(y2-y1); putpixel(x,round(y),c); for(int i=y1;i<=y2;i++) { y++; x=x+k; putpixel(round(x),y, c); } } - Áp dụng giải thuật, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(15, 27), B(22, 35). Stt 1 2 3 4 5 6 7 8 9 x 15 16 17 18 18 19 20 21 22 y 27 28 29 30 31 32 33 34 35 4. - Giải thuật DDA sinh đường thẳng với hệ số góc m > 1, Dx >0. void Mid_line(int x1, int y1, int x2, int y2, int c) { int x, y, dx, dy,d; y = y1; dx = x2 - x1; dy = y2 - y1; d= 2dx - dy; for (y=y1; y<=y2; y++) { putpixel(x, y, c); if (d < 0) d = d + 2dx; else { x ++; d = d + 2dx - 2dy; } } } - Áp dụng giải thuật, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(12, 19); B(18, 27). Stt 1 2 3 4 5 6 7 8 9 x 12 13 14 14 15 16 17 17 18 y 19 20 21 22 23 24 25 26 27 P 4 0 -4 8 4 0 -4 8 4 5. Giải thuật Bresenham sinh đường thẳng với hệ số góc m > 1, Dx >0. void Bre_line(int x1, int y1, int x2, int y2, int c) {int x, y, dx, dy,p,const1,const2; y = y1; dx = x2 - x1; dy = y2 - y1; p = 2*dx - dy; const1 = 2*dx; const2 = 2*(dx-dy); for (y=y1; y<=y2; y++) { putpixel(x, y, c); if (p < 0) p += const1; // p=p + 2dx else { p +=const2; //p=p+2dx-2dy x++; } } } - Áp dụng giải thuật, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(12, 19); B(18, 27). Stt 1 2 3 4 5 6 7 8 9 x 20 21 21 22 23 23 24 24 25 y 22 23 24 25 26 27 28 29 30 P 2 -4 6 0 -6 4 -2 8 2 Chương 3 CÁC GIẢI THUẬT ĐỒ HOẠ CƠ SỞ 3.1. Hệ toạ độ và mô hình chuyển đổi 3.1.1. Các hệ thống tọa độ trong đồ họa 1) Hệ toạ độ thực (WCS – World Coordinate System) Hệ toạ độ của đối tượng được các chương trình ứng dụng sử dụng để mô tả toạ độ các đối tượng trong thế giới thực. Đơn vị trong hệ thống toạ độ phụ thuộc vào không gian và kích thước của đối tượng được mô tả: mm, m, km… Hình 3.1 Hệ toạ độ thực 2) Hệ toạ độ thiết bị (DCS – Device Coordinate System) Là hệ thống toạ độ của thiết bị nơi hiển thị hình ảnh và không gian của đối tượng mà ứng dụng mô tả. Không gian của hệ thống của toạ độ này chính là kích thước của thiết bị hiển thị được sử dụng. Ví dụ: màn hình VGA 640x480, SVGA 600x800… Hình 3.2 DCS – Device Coordinate System 3) Hệ toạ độ thiết bị chuẩn (NDCS – Normalized Device Coordinate System) Chuyển đổi đối tượng từ không gian thực vào toạ độ thiết bị hiển thị. Phần mềm đồ hoạ được viết sẽ thực hiện sự chuyển đổi mà chưa thể xác định rò kích thước của thiết bị cũng như độ phân giải. Ta có công cụ độc lập với thiết bị nhằm mô tả vùng hiển thị ra hệ toạ độ thiết bị chuẩn hoá. Coi NDCS như hệ toạ độ thiết bị có kích thước màn hình hiển thị là một hình vuông có cạnh là một đơn vị (1x1). Hình 3.3 NDCS – Normalized Device Coordinate System - Qui trình để chuyển đổi các đối tượng trong WCS sang NDCS được gọi là phép ánh xạ cửa sổ sang cổng xem hay phép biến đổi chuẩn hoá (Window to Viewport mapping or Normalization Transformation) - Qui trình có thể áp các toạ độ thiết bị hiển thị chuẩn hoá sang các thiết bị rời rạc được gọi là phép biến đổi trạm làm việc (Workstation Transformation) 3.1.2. Phép chuyển đổi - Một cửa sổ (window) được chỉ định bởi bốn toạ độ thực (WCS): Xwmin, Xwmax, Ywmin, Ywmax - Một cổng xem (viewport) được mô tả bởi bốn toạ độ thiết bị chuẩn hoá (NDCS): Xvmin, Xvmax, Yvmin, Yvmax a) b) Hình 3.4 a)Đối tượng cổng xem; b)Đối tượng trong cửa sổ Mục đích của phép ánh xạ này là chuyển đổi các toạ độ thực (Xw,Yw) của một điểm tuỳ ý sang thiết bị chuẩn hoá tương ứng (Xv,Yv). Để giữ lại khoảng cách của điểm trong cổng xem bằng với khoảng cách của điểm trong cửa sổ, với yêu cầu: 𝑥𝑣 − 𝑥𝑣𝑚𝑖𝑛 𝑥𝑣𝑚𝑎𝑥 − 𝑥𝑣𝑚𝑖𝑛 𝑦𝑣 − 𝑦𝑣𝑚𝑖𝑛 𝑦𝑣𝑚𝑎𝑥 − 𝑦𝑣𝑚𝑖𝑛 𝑥𝑤 − 𝑥𝑤𝑚𝑖𝑛 = 𝑥𝑤𝑚𝑎𝑥 − 𝑥𝑤𝑚𝑖𝑛 𝑦𝑤 − 𝑦𝑤𝑚𝑖𝑛 = 𝑦𝑤𝑚𝑎𝑥 − 𝑦𝑤𝑚𝑖𝑛 𝑥𝑣 = 𝑥𝑣𝑚𝑖𝑛 + (𝑥𝑤 − 𝑥𝑤𝑚𝑖𝑛 )𝑠𝑥 𝑦𝑣 = 𝑦𝑣𝑚𝑖𝑛 + (𝑦𝑤 − 𝑦𝑤𝑚𝑖𝑛 )𝑠𝑦 𝑥𝑣𝑚𝑎𝑥 − 𝑥𝑣𝑚𝑖𝑛 𝑥 𝑠𝑥 = 𝑤𝑚𝑎𝑥 − 𝑥𝑤𝑚𝑖𝑛 𝑦𝑣𝑚𝑎𝑥 − 𝑦𝑣𝑚𝑖𝑛 𝑦 𝑠𝑦 = 𝑤𝑚𝑎𝑥 − 𝑦𝑤𝑚𝑖𝑛 3.2. Các giải thuật xén tỉa 3.2.1. Khái niệm Xén tỉa là tiến trình xác định các điểm của một đối tượng nằm trong hay ngoài cửa sổ hiển thị. Nằm trong được hiển thị, nằm ngoài loại bỏ. Việc loại từng điểm ảnh của đối tượng thường chậm nhất là khi đối tượng mà phần lớn nằm ngoài cửa sổ hiển thị. 3.2.2. Các giải thuật xén tỉa đoạn thẳng 1) Bài toán: Cho cửa sổ với các đường biên có tọa độ góc dưới trái và góc trên phải lần lượt là (xwmin, ywmin), (xwmax, ywmax) và đoạn thẳng cho bởi 2 điểm P1(x1, y1), P2(x2, y2). Hãy xác định phần hiển thị của đoạn thẳng trong cửa sổ trên. 2) Ý tưởng: Hình 3.5. Điểm và đoạn thẳng bị cắt khỏi cửa sổ Việc cắt các điểm khỏi cửa sổ được hiểu đơn giản là chúng ta kiểm tra các giá trị tọa độ để xác định xem chúng có nằm bên trong biên không. Một điểm ở vị trí (x,y) được giữ lại để chuyển đổi sang vùng quan sát nếu nó thỏa các bất phương trình sau: xwmin ≤ x ≤ xwmax, ywmin ≤ y ≤ ywmax Nếu điểm nào không thỏa một trong bốn bất phương trình trên, nó bị cắt bỏ. Trong hình 3.5, điểm P1 được giữ lại, trong khi điểm P2 bị cắt bỏ. Hình 3.5 minh họa các quan hệ có thể có giữa các vị trí đoạn thẳng với biên cửa sổ. Chúng ta kiểm tra một đoạn thẳng xem có bị cắt hay không bằng việc xác định xem hai điểm đầu mút đoạn thẳng là nằm trong hay nằm ngoài cửa sổ. Một đoạn thẳng với cả hai đầu nằm trong cửa sổ thì được giữ lại hết, như đoạn từ P5 đến P6. Một đoạn với một đầu nằm ngoài (P9) và một đầu nằm trong (P10) sẽ bị cắt bớt tại giao điểm với biên cửa sổ (P‘9). Các đoạn thẳng có cả hai đầu đều nằm ngoài cửa sổ, có thể rơi vào hai trường hợp: toàn bộ đoạn thẳng đều nằm ngoài hoặc đoạn thẳng cắt hai cạnh cửa sổ. Đoạn từ P3 đến P4 bị cắt bỏ hoàn toàn. Nhưng đoạn từ P7 đến P8 sẽ được giữ lại phần từ P‘7 đến P‘8. Thuật toán clipping đường (line-clipping) xác định xem đoạn nào toàn bộ nằm trong, đoạn nào bị cắt bỏ hoàn toàn hay bị cắt một phần. Đối với các đoạn bị cắt bỏ một phần, các giao điểm với biên cửa sổ phải được tính. Vì một hình ảnh có thể chứa hàng ngàn đoạn thẳng, việc xử lý clipping nên được thực hiện sao cho có hiệu quả nhất. Trước khi đi tính các giao điểm, một thuật toán nên xác định rò tất cả các đoạn thẳng được giữ lại hoàn toàn hoặc bị cắt bỏ hoàn toàn. Với những đoạn được xem xét là bị cắt bỏ, việc xác định các giao điểm cho phần được giữ lại nên được thực hiện với sự tính toán ít nhất. 3) Giải thuật Cohen Sutherland Outcode Một tiếp cận để cắt các đoạn là dựa trên cơ chế đánh mã được phát triển bởi Cohen và Sutherland. Mọi điểm ở hai đầu mút đoạn thẳng trong hình ảnh sẽ được gán một mã nhị phân 4 bit, được gọi là mã vùng (region code) như ở hình 3.6, giúp nhận ra vùng tọa độ của một điểm. Các vùng này được xây dựng dựa trên sự xem xét với biên cửa sổ. Mỗi vị trí bit trong mã vùng được dùng để chỉ ra một trong bốn vị trí tọa độ tương ứng của điểm so với cửa sổ: bên trái (left), phải (right), trên đỉnh (top), dưới đáy (bottom). Việc đánh số theo vị trí bit trong mã vùng từ 1 đến 4 cho từ phải sang trái, các vùng tọa độ có thể liên quan với vị trí bit như sau:
Các Vị Trí Đối Xứng Trên Đường Tròn (C) Tương Ứng Với (X,y)
Mô Tả Giải Thuật Sinh Đường Ellipse
Đồ họa máy tính - 8
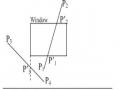Các Mã Vùng Nhị Phân Cho Các Điểm Đầu Mút Đoạn Thẳng Được Dùng Để Định Nghĩa Các Vùng Tọa Độ Liên Hệ Với Một Cửa Sổ.
Các Trường Hợp Xén Tỉa Một Cạnh Của Cửa Sổ Với Biên Cửa Sổ
Đồ họa máy tính - 12
