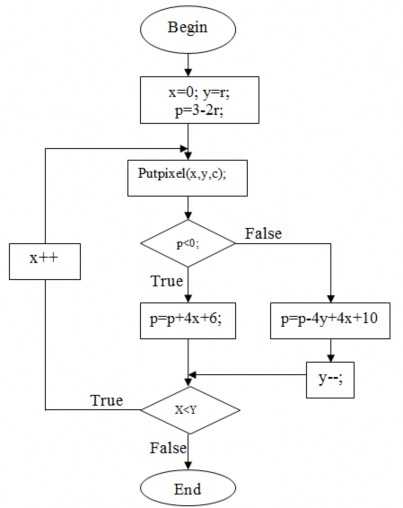
procedure Circle(r, color: integer)
begin
var: x, y, p
x :=0, y :=r;
p :=3 - 2*r; while (x<=y) do
begin
put8pixel(x, y, color);
if (p<0)then p:=p + 4*x + 6 else
begin
p:=p + 4*(x-y) + 10; y:=y-1;
end; x:=x+1;
end;
end;
Bước | xi | yi | p |
0 | 0 | 15 | -27 |
1 | 1 | 15 | -21 |
2 | 2 | 15 | -11 |
3 | 3 | 15 | 3 |
4 | 4 | 14 | -35 |
5 | 5 | 14 | -13 |
6 | 6 | 14 | 13 |
7 | 7 | 13 | -9 |
8 | 8 | 13 | 25 |
9 | 9 | 12 | 15 |
10 | 10 | 11 | 13 |
Có thể bạn quan tâm!
-
 Ảnh Cánh Tay Robot Được Cấu Tạotừ Các Đối Tượng Đồ Họa Cơ Sở
Ảnh Cánh Tay Robot Được Cấu Tạotừ Các Đối Tượng Đồ Họa Cơ Sở -
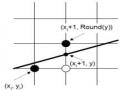
 Các Điểm X I 1 , Y I 1 Chọn Ở Bước (I+1) Cho Trường Hợp Đoạn Thẳng Có Hệ Số Góc 0
Các Điểm X I 1 , Y I 1 Chọn Ở Bước (I+1) Cho Trường Hợp Đoạn Thẳng Có Hệ Số Góc 0 -
 Các Vị Trí Đối Xứng Trên Đường Tròn (C) Tương Ứng Với (X,y)
Các Vị Trí Đối Xứng Trên Đường Tròn (C) Tương Ứng Với (X,y) -
 Đồ họa máy tính - 8
Đồ họa máy tính - 8 -
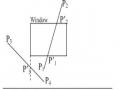
 A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ
A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ -
 Các Mã Vùng Nhị Phân Cho Các Điểm Đầu Mút Đoạn Thẳng Được Dùng Để Định Nghĩa Các Vùng Tọa Độ Liên Hệ Với Một Cửa Sổ.
Các Mã Vùng Nhị Phân Cho Các Điểm Đầu Mút Đoạn Thẳng Được Dùng Để Định Nghĩa Các Vùng Tọa Độ Liên Hệ Với Một Cửa Sổ.
Xem toàn bộ 240 trang tài liệu này.
Ví dụ 2.4. Tính các điểm được vẽ trên đường tròn có bán kính bằng 15 Ta có: x = 0, y = 15, p = 3 - 2R = -27
2.5. Giải thuật sinh Elippse
2.5.1. Giải thuật Midpoint
Tương tự thuật toán vẽ đường tròn, sử dụng thuật toán Midpoint để vẽ, chỉ cần vẽ 1/4 Ellipse, sau đó lấy đối xứng qua các trục tọa độ sẽ vẽ được toàn bộ Ellipse. Sự khác biệt so với thuật toán vẽ đường tròn là ta phải vẽ 2 phần (chia cung từ (0,b) đến (a,0) tại Q, có độ dốc -1) (Hình 2.16)
Trên phần 1: x thay đổi thì y thay đổi theo Trên phần 2: y thay đổi thì x thay đổi theo
Q,
độ
Hình 2.16Mô tả giải thuật sinh đường Ellipse
Xét Ellipse có tâm O, các bán kính là a và b, phương trình là:
x2 y2
+ Xét trên phần 1:
a2 + b2 =1
Bắt đầu từ điểm (0, b), giả sử bước thứ i điểm (xi,yi) đã vẽ, bước thứ i + 1 ta chọn điểm A(xi+1, yi) hoặc điểm B(xi+1,yi-1).
Ta có:
pi = f(xi+1,yi-1/2) = b2 (xi+1)2 + a2(yi-1/2)2 -a2b2
pi+1 = f(xi+1+1,yi+1-1/2) = b2(xi+1+1)2 + a2(yi+1-1/2)2 -a2b2
pi+1 - pi = b2((xi+1+1)2 - (xi+1)2 )+ a2((yi+1-1/2)2 - (yi-1/2)2) ( do xi+1 = xi+1) pi+1 = pi + b2(2xi+ 3) + a2((yi+1-1/2)2 - (yi-1/2)2 )
- Nếu pi< 0 chọn A với xi+1 = xi+1 và yi+1 = yi do đó: pi+1 = pi + b2(2xi +3)
- Nếu pi ≥ 0 chọn B với xi+1 = xi+1 và yi+1=yi -1 do đó: pi+1 = pi + b2(2xi +3) + a2((yi-1 -1/2)2 - (yi-1/2)2 )
= pi + b2(2xi +3) + a2(-3yi +9/4 +yi -1/4)
= pi + b2(2xi +3) + a2(-2yi +2)
Hay pi+1 = pi + b2(2xi +3) + a2(-2yi +2)
- Tính p1 tại (0,b)
p1 = f(x1+1, y1-1/2) = b2 + a2(b-1/2)2 -a2b2 p1 = b2 - a2b +a2/4
+ Xét trên phần 2:
Ta lấy tọa độ của điểm vẽ sau cùng trong phần 1 của đường cong để tính giá trị ban đầu cho phần 2.
Giả sử điểm (xk,yk) vừa chuyển quét cuối cùng của phần 1 nhập vào bước j cho phần 2 (xj,yj). Điểm vẽ kế tiếp có thể là: C(xj,yj-1) hoặc D(xj+1, yj-1)
Ta có:
qj = f(xj+1/2,yj-1) = b2(xj+1/2)2 + a2(yj-1)2 -a2b2
qj+1 = f(xj+1+1/2,yj+1-1) = b2(xj+1+1/2)2 + a2(yj+1-1)2 -a2b2
qj+1 - qj = b2((xj+1+1/2)2 - (xj+1/2)2 )+ a2((yj+1-1)2 - (yj-1)2 ) (do yi+1 = yi - 1) qj+1 = qj + b2((xj+1+1/2)2 - (xj+1/2)2 )+ a2(3 – 2yi)
- Nếu qj< 0 chọn D với yj+1=yj-1 và xj+1=xj +1 qj+1 = qj + b2((xj+3/2)2 - (xj+1/2)2 ) +a2 (-2yj +3) qj+1 = qj + b2(3xj +9/4- xj -1/4) +a2 (-2yj +3) Hay qj+1 = qj + b2(2xj +2) +a2 (-2yj +3)
- Nếu qj ≥ 0 chọn C với yj+1=yj -1 và xj+1= xj Hay qj+1 = qj + a2(3 - 2yj )
- Tính q1:
q1 = f(xk+1/2,yk -1) = b2(xk+1/2)2 + a2(yk-1)2 -a2b2
Thủ tục sinh Ellipse:
procedure Ellipse(xc, yc, a, b, color: integer) begin
var x, y, fx, fy, a2, b2, p: integer; x := 0; y := b;
a2 := a * a; b2 := b * b; fx := 0;
fy := 2 * a2 * y; plot(xc, yc, x,y, color);
p := ROUND(b2-(a2*b)+(0.25*a));
while (fx < fy) do begin
x:= x +1;
fx := 2*b2;
if (p<0) then p := p +b2*(2*x +3) else begin
y := y -1;
p := p + b2*(2*x +3) + a2*(-2*y +2);
a2*b2);
fy := fy - 2*a2; end;
plot(xc, yc, x, y, color); end;
p := ROUND(b2*(x+0.5)*(x+0.5) + a2*(y-1)*(y-1) -
{b2(x+1/2)2+a2(y-1)2 - a2b2}
while (y>0) do begin
y := y -1;
fy :=fy - 2*a2;
if (p>=0) then p := p + a2*(3 - 2*y)
else
end; end;
begin
x := x +1;
fx := fx + 2*b2;
p := b2*(2*x+2) + a2*(-2*y +3); end;
plot(xc, yc, x, y, color);
2.5.2. Giải thuật Bresenham
Giả sử điểm (xi,yi) đã được vẽ. Điểm tiếp theo cần chọn sẽ là (xi+1,yi) hoặc (xi+1,yi-1)
Thay (xi
Đặt:
+1) vào phương trình Elippse ta được: y2 = - b
2
a 2
.(xi
+1)2 + b2
2
d = yi2 - y2 = y 2 + b .(x
+1)2 -b2
1 i a 2i
2
d = y2 - (y -1)2 = - b .(x +1)2 + b2 - (y
-1)2
2
2 i a 2 i i
p = d
- d = 2.[
b .(x
+1)2 - b2] + 2.(y 2 + y ) -1
i 1 2
p = 2[
a 2
2
b .(x
i
+1)2 - b2] + 2.(y
i i
2 + y ) -1
i+1
a 2 i+1
i+1
i+1
Suy ra:
2
p - p = 2 b
[(x +1)2 - (x
+1)2] + 2.( y 2 - y 2 + y
- y ) (**)
2
i+1 i
*Nhận xét:
i+1 i
a
i+1 i
i+1 i
pi< 0: Chọn yi+1 = yi
(**) pi+1
= pi
+ 2. b
2
a 2
.(2x + 3)
pi 0: Chọn yi+1 = yi -1
(**) pi+1
= pi
+ 2. b
2
a 2
.(2x + 3) - 4yi
Với điểm đầu tiên (0,b), ta có:
p1
= 2 b
2
a 2
- 2b + 1
Từ đó, ta có thủ tục vẽ Ellipse như sau:
Procedure Ellipse(xc,yc,a,b:Integer;Color:Byte); Var p,a2,b2:real;
x,y:integer;
(*-------------------*)
Procedure VeDiem; Begin
PutPixel(xc+x,yc+y,Color); PutPixel(xc-x,yc+y,Color); PutPixel(xc-x,yc-y,Color); PutPixel(xc+x,yc-y,Color);
End;
(*-------------------*)
Begin
a2:=a*a; b2:=b*b;
{Nhanh 1} x:=0; y:=b;
p:=2*b2/a2 - 2*b + 1; While (b2/a2)*(x/y)<1 do
Begin
VeDiem;
If p<0 then p:=p + 2*(b2/a2)*(2*x+3) else Begin
p:=p - 4*y + 2*(b2/a2)*(2*x+3); y:=y-1;
End;
x:=x+1;
End;
{Nhanh 2} y:=0; x:=a;
p:=2*(a2/b2) - 2*a + 1; While (a2/b2)*(y/x)<=1 do
Begin
VeDiem;
If p<0 then p:=p + 2*(a2/b2)*(2*y+3) else Begin
p:=p - 4*x + 2*(a2/b2)*(2*y+3); x:=x-1;
End; y:=y+1;
End;
End;
2.6. Giải thuật sinh đa giác
Việc biểu diễn đa giác thông qua:
- Tập các đoạn thẳng
- Tập các điểm thuộc đa giác Các loại đa giác:
Hình 2.17 Các loại đa giác
Đa giác lồi: Là đa giác có đường thẳng nối bất kỳ 2 điểm bên trong nào của đa giác đều nằm trọn trong đa giác.
Đa giác không lồi là đa giác lòm.
Các đường thẳng bao đa giác - cạnh của đa giác. Các điểm giao của cạnh - đỉnh của đa giác. Thông tin cần thiết để xác định đa giác:
- Số cạnh
- Tọa độ các đỉnh của đa giác Giải thuật sinh đa giác:
procedure Polygon (arrayx, arrayy,n) begin
//n là số đỉnh của đa giác
//arrayx là mảng hoành độ các đỉnh của đa giác
//arrayy là mảng tung độ các đỉnh của đa giác if (n<3) then exit;
for i: = 1 to n – 1 do
line(arrayx[i],arrayy[i], arrayx[i+1], arrayy[i+1]); line(arrayx[i+1],arrayy[i+1], arrayx[1], arrayy[1]);
end;
2.7. Giải thuật sinh ký tự
Trong màn hình text, truy xuất các ký tự trên màn hình được hỗ trợ bởi phần cứng. Các ký tự được lưu trữ trong bộ nhớ ROM, dưới dạng bitmap hay các ma trận ảnh. Phần cứng sẽ đưa ký tự lên màn hình tại ví trí xác định, tính toán cuốn trang và xuống dòng.
Trong đồ hoạ:
+ Vector: Định nghĩa các ký tự theo những đường cong mềm bao ngoài của chúng, tốn kém về mặt tính toán. Biểu diễn ký tự vector có một số đặc điểm sau:
Phức tạp (tính toán phương trình) Lưu trữ gọn nhẹ
Các phép biến đổi dựa vào các công thức biến đổi
Kích thước phụ thuộc vào môi trường ( không có kích thước cố định)

Hình 2.18 Ký tự vector