Ta có dạng tổng quát của phương trình đường thẳng:
Ax By C 0
với Đặt
A y2 y1 , B x 2 x1 , C x 2 y1 x1 y2
Fx, y Ax By C , ta có nhận xét :
<0 Nếu (x, y) nằm phía trên đường thẳng
Fx,y=0 Nếu x, y thuộc đường thẳng
>0 Nếu x, y nằm phía dưới đường thẳng
Lúc này việc chọn các điểm S, P ở trên được đưa về việc xét dấu của
i
p 2FMidPoint
2 x
Fi
1, yi
1 .
2
Nếu pi 0 , điểm MidPoint nằm phía trên đoạn thẳng. Lúc này điểm thực Q
nằm dưới điểm MidPoint nên ta chọn S, tức là
yi1 yi .
Ngược lại, nếu pi 0 , điểm MidPoint nằm phía dưới đoạn thẳng. Lúc này điểm
thực Q nằm trên điểm MidPoint nên ta chọn P, tức là Mặt khác:
yi1 yi 1.
p p
2F x
1, y
1 2F x 1, y 1
i1 i
i1
i1 i i
2
2
p p
1
1
1
1
i1
i 2A x i1
Byi1
2
C
2A x i
B yi
2
C
pi1
pi
2A 2By
i1
yi
2Dy 2Dxy
i1
yi
Vậy:
pi1 pi 2Dy , nếu
pi 0 do ta chọn yi1 yi .
pi1 pi 2Dy 2Dx , nếu
pi 0
do ta chọn yi1 yi 1.
Ta tính giá trị
p0 ứng với điểm ban đầu x 0 , y0 : vì x 0 , y0 là điểm thuộc đoạn
thẳng nên Ax0 By 0 C 0
p
1, y
1
1
1
0 2F x 0
0 2A x 0
2
B y0
2
C
p0 2Ax0 By0 C 2A B 2A B 2Dy Dx
Nhận xét: Thuật toán MidPoint cho kết quả tương tự như thuật toán Bresenham.
2.4. Giải thuật sinh đường tròn
2.4.1 Nguyên lý chung
Phương trình đường tròn có tâm là gốc tọa độ, bán kính R là:
x2 y2 R2 . Từ
R 2 x2
phương trình này ta có thể đưa về dạng y
. Để vẽ các đường tròn có tâm
xC, yCbất kì, đơn giản chỉ cần tịnh tiến các điểm sau khi vẽ xong đường tròn có tâm là gốc tọa độ theo vector tịnh tiến xC, yC.
Do tính đối xứng nên để vẽ toàn bộ đường tròn, ta chỉ cần vẽ cung ¼ đường tròn sau đó lấy đối xứng để xác định các điểm còn lại.
Một trong những cách đơn giản nhất là cho x chạy từ 0 đến R, sau đó tính y từ công thức trên (chỉ lấy giá trị dương) rồi làm tròn để xác định giá trị nguyên tương ứng. Cách làm này không hiệu quả do gặp phải các phép toán nhân và lấy căn làm hạn
chế tốc độ, ngoài ra đường tròn vẽ ra theo cách này có thể không liền nét (trừ trường hợp R lớn) khi x gần R (do chỉ có một giá trị y duy nhất cho một giá trị x). Chúng ta có thể khắc phục điều này bằng cách điều chỉnh đối tượng thay đổi là x (rồi tính y theo x) hay y (rồi tính x theo y) tùy vào giá trị tuyệt đối của hệ số góc đường tròn là lớn hơn hay nhỏ hơn 1, nhưng cách làm này đòi hỏi thêm các phép tính toán và kiểm tra nên làm cho thuật toán phức tạp thêm (hình 2.12)
Một cách tiếp cận khác là vẽ các điểm
Rcosθ, Rsinθ,
với θ chạy từ 00 đến
900. Cách này sẽ khắc phục hạn chế đường không liền nét của thuật toán trên, tuy nhiên điểm hạn chế chính của thuật toán này đó là chọn bước nhảy cho θ như thế nào cho phù hợp khi bán kính thay đổi.
(0,17)
(17,0)
Hình 2.13Đường tròn vẽ ra không liền nét
2.4.2 Thuật toán MidPoint
(-x,y)
(x,y)
(-y,x)
(y,x)
(-y,-x)
R
2 (y,-x)
(-x,-y)
(x,-y)
Do tính đối xứng của đường tròn (C) nên ta chỉ cần vẽ cung (C1/8) là cung 1/8 đường tròn, sau đó lấy đối xứng. Cung (C1/8) được mô tả như sau (cung của phần tô xám trong hình vẽ):
2
0 x R
2
2
R y R
2
Hình 2.14 Các vị trí đối xứng trên đường tròn (C) tương ứng với (x,y)
Như vậy nếu có (x, y) (C1/8) thì các điểm (y, x), (y,-x), (x,-y), (-x,-y), (-y,-x), (-y,x), (-x,y) sẽ thuộc (C).
i
i
Chọn điểm bắt đầu để vẽ là điểm (0, R). Dựa vào hình vẽ, nếu x , y là điểm
nguyên đã tìm được ở bước thứ i, thì điểm xi1, yi1 ở bước thứ (i+1) là sự lựa chọn giữa S và P.
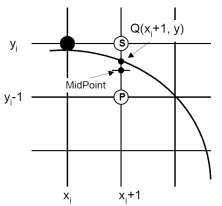
Hình 2.15 Thuật toán MidPoint vẽ đường tròn
xi1 xi 1
Như vậy: y
yi
y
1
i1
i
Tương tự như thuật toán MidPoint vẽ đoạn thẳng, việc quyết định chọn một trong hai điểm S và P sẽ được thực hiện thông qua việc xét dấu của một hàm nào đó tại điểm MidPoint là điểm nằm giữa chúng.
Đặt
Fx, y x 2 y2 R 2 , ta có :
<0 Nếu (x, y) nằm trong đường tròn Fx,y=0 Nếu x, y nằm trên đường tròn
>0 Nếu x, y nằm ngoài đường tròn
Xét pi
FMidPoint F x
i
1, yi
1 . Ta có:
2
Nếu
pi 0 , điểm MidPoint nằm trong đường tròn. Lúc này điểm thực Q gần S
hơn nên ta chọn S, tức là yi1 yi .
Ngược lại, nếu pi 0 , điểm MidPoint nằm ngoài đường tròn. Lúc này điểm thực Q gần P hơn nên ta chọn P, tức là yi1 yi 1.
Mặt khác:
p p
F x
1, y
1 F x 1, y 1
i1 i
i1
i1 i i
2
2
2 1
2
22 1
2
2
pi1 pi
x i1 1 yi 1 2
R x i 1 yi 2 R
2 1
2
22 1
2
2
pi 1 pi
x i 2 yi1 2 R x i 1 yi 2 R
pi1 pi
2x i 3 y y y
2 2
i1
i
i1
yi
Vậy:
pi1 pi 2xi 3, nếu
pi 0 do ta chọn yi1 yi .
pi1 pi 2xi 2yi 5, nếu
pi 0
do ta chọn yi1 yi 1.
Ta tính giá trị p0ứng với điểm ban đầu x0,y0
được suy ra là (1, R – 1/2). Theo công thức:
là (0, R) và trung điểm tiếp theo
p F x
0 0
1, y0
1
2
F1, R 1
2
= 1 + (R2 – R + 1/4) –R2
= 5 R 4
Lưu đồ thuật toán và chương trình cài đặt thuật toán MidPoint vẽ đường tròn
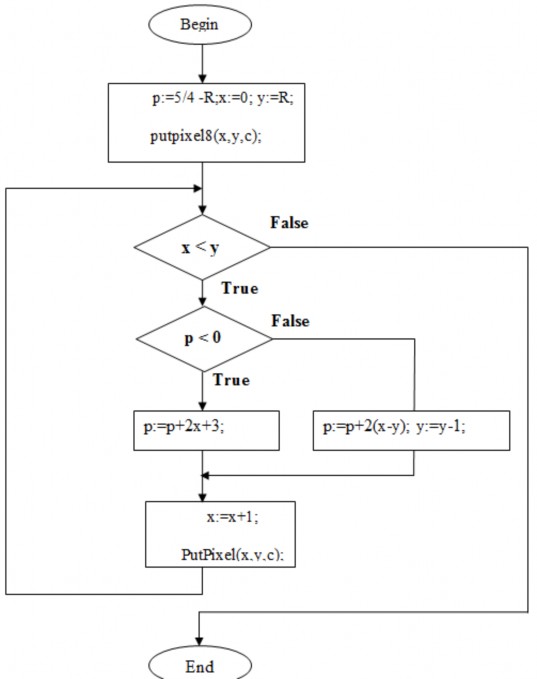
// Giải thuật vẽ 8 điểm đối xứng
procedureput8Pixel(x, y, Color: integer)
{
putpixel(x, y, Color);putpixel(y, x, Color); putpixel(y,-x, Color);putpixel(x,-y, Color); putpixel(-x,-y, Color);putpixel(-y,-x, Color); putpixel(-y, x, Color); putpixel(-x, y, Color);
}
//Giải thuật Midpoint
procedure CircleMidPoint (R, color: integer)
begin
var x, y, p:integer; x := 0;
y := R;
put8Pixel(x, y, color); p:= 1 - R; // 5/4-R
while (x < y) do begin
if (p < 0) then p := 2*x + 3 else
begin
p :=p+ 2*(x -y) + 5; y := y -1;
end; x++;
put8Pixel(x, y, color); end;
end;
Ví dụ 2.3. Tính các điểm được vẽ trên đường tròn có bán kính bằng 15 và tâm tại gốc tọa độ.
Ta có: x = 0, y = 15, p = 1- R = -14
xi | yi | p | |
0 | 0 | 15 | -14 |
1 | 1 | 15 | -11 |
2 | 2 | 15 | -6 |
3 | 3 | 15 | 1 |
4 | 4 | 14 | -18 |
5 | 5 | 14 | -7 |
6 | 6 | 14 | 6 |
7 | 7 | 13 | -5 |
8 | 8 | 13 | 12 |
9 | 9 | 12 | 7 |
10 | 10 | 11 | 6 |
Có thể bạn quan tâm!
-
 Các Thành Phần Phần Cứng Của Hệ Tọa Độ Tương Tác
Các Thành Phần Phần Cứng Của Hệ Tọa Độ Tương Tác -
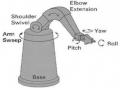
 Ảnh Cánh Tay Robot Được Cấu Tạotừ Các Đối Tượng Đồ Họa Cơ Sở
Ảnh Cánh Tay Robot Được Cấu Tạotừ Các Đối Tượng Đồ Họa Cơ Sở -
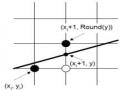
 Các Điểm X I 1 , Y I 1 Chọn Ở Bước (I+1) Cho Trường Hợp Đoạn Thẳng Có Hệ Số Góc 0
Các Điểm X I 1 , Y I 1 Chọn Ở Bước (I+1) Cho Trường Hợp Đoạn Thẳng Có Hệ Số Góc 0 -
 Mô Tả Giải Thuật Sinh Đường Ellipse
Mô Tả Giải Thuật Sinh Đường Ellipse -
 Đồ họa máy tính - 8
Đồ họa máy tính - 8 -
 A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ
A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ
Xem toàn bộ 240 trang tài liệu này.
11 | 10 | 9 |
2.4.3 Giải thuật Bresenham
Giả sử (xi,yi) đã vẽ được. Cần chọn điểm kế tiếp là (xi +1,yi) hoặc (xi +1,yi -1) Từ phương trình: x2 + y2 = R2 ta tính được giá trị y thực ứng với xi +1 là:
y2 = R2 - (xi +1)2 (3.1)
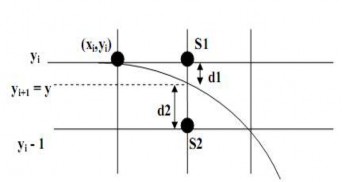
Hình 2.14 Thuật toán Bresenham sinh đường tròn
Đặt: d1 = yi2 - y2 = yi2 - R2 + (xi + 1)2
d2 = y2 - (yi - 1)2 = R2 - (xi + 1)2 - (yi - 1)2
Suy ra:
pi = d1 - d2 = 2.(xi + 1)2 + yi2 + (yi - 1)2 - 2R2 (3.2)
pi+1 = 2.(xi+1 + 1)2 + y2i+1 + (yi+1 - 1)2 - 2R2 (3.3)
Từ (3.2) và (3.3) ta có:
pi+1 - pi = 4xi + 6 + 2.(y2i+1 - yi2) - 2.(yi+1 - yi)
pi+1 = pi + 4xi + 6 + 2.(y2i+1 - yi2) - 2.(yi+1 - yi) (3.4)
tròn
* Nhận xét:
Nếu pi< 0: ta chọn yi+1 = yi thay vào (3.4) pi+1 = pi + 4xi + 6
Nếu pi 0: chọn yi+1 = yi– 1 thay vào (3.4) pi+1 = pi + 4.(xi - yi) + 10 Ta chọn điểm đầu tiên cần vẽ (0, R), theo (3.2) ta có: p1 = 3 - 2R
Lưu đồ thuật toán và chương trình cài đặt thuật toán Bresenham vẽ đường