Đồ họa máy tính - 12

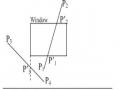
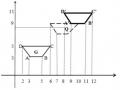
9. Giả sử cạnh AB là một cạnh của cửa sổ xén tỉa, P0 P1..... PN-1 là danh sách các đỉnh của đa giác cần xén tỉa (đa giác lồi hướng dương). Theo giải thuật Hogman thì Pi-1 và Pi đều nằm bên phải của cạnh AB thì đỉnh được đưa vào danh sách của đa giác sau khi xén tỉa(VertexOutput) là:

[a]--Pi-1

[b]--Pi

[c]--Cả Pi-1 và Pi

[d]--Không có đỉnh nào

10. Giả sử cạnh AB là một cạnh của cửa sổ xén tỉa, P0 P1..... PN-1 là danh sách các đỉnh của đa giác cần xén tỉa (đa giác lồi hướng dương). Theo giải thuật Hogman thì Pi-1 nằm bên phải và Pi nằm bên trái của cạnh AB thì đỉnh được đưa vào danh sách của đa giác sau khi xén tỉa (VertexOutput) là:

[a]--Giao điểm I của Pi-1 Pi với cạnh AB và Pi [b]--Giao điểm I và Pi-1

[c]--Chỉ có giao điểm I [d]--Cả Pi-1 và Pi

11. Giả sử cạnh AB là một cạnh của cửa sổ xén tỉa, P0 P1..... PN-1 là danh sách các đỉnh

của đa giác cần xén tỉa (đa giác lồi hướng dương). Theo giải thuật Hogman thì Pi-1 nằm bên trái và Pi nằm bên phải của cạnh AB thì đỉnh được đưa vào danh sách của đa giác sau khi xén tỉa (VertexOutput) là:

Có thể bạn quan tâm!

• A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ
• Các Mã Vùng Nhị Phân Cho Các Điểm Đầu Mút Đoạn Thẳng Được Dùng Để Định Nghĩa Các Vùng Tọa Độ Liên Hệ Với Một Cửa Sổ.
• Các Trường Hợp Xén Tỉa Một Cạnh Của Cửa Sổ Với Biên Cửa Sổ
• Phương Pháp Biểu Diễn Đối Tượng Trong Không Gian Hai Chiều
• Phép Quay Quanh Tâm Là Điểm Bất Kì. (A) Đối Tượng Trước Khi Biến Đổi,(B) Sau Khi Tịnh Tiến Về Gốc Tọa Độ, (C) Sau Khi Quay Góc Α, (D) Sau Khi Tịnh
• Xây Dựng Công Thức Biến Đổi Đối Tượng Khi Thực Hiện Các Phép Biến Đổi:

Xem toàn bộ 240 trang tài liệu này.

[a]--Cả Pi-1 và Pi

[b]--Giao điểm I của Pi-1 Pi với cạnh AB và Pi [c]--Giao điểm I của Pi-1 Pi với cạnh AB

[d]--Không có đỉnh nào

12. Cho cửa sổ cắt tỉa hình chữ nhật có góc trái dưới L(3,1), góc phải trên R(7,4). Cho đoạn IJ có toạ độ là I(8,2) và J(8,3), dùng giải thuật Lyangbarsky tính các giá trị P1 ,

P2 , P3 và P4

[a]--P1 =0, P2 =0, P3 = -1 và P4 =1

[b]--P1 = -1, P2 = 1, P3 = 0 và P4 = 0 [c]--P1 = 1, P2 = - 1, P3 = 0 và P4 = 0 [d]--P1 = 1, P2 = - 1, P3 = 1 và P4 = -1

13. Trong các câu nói sau câu nào sai ? (theo giải thuật Cohen Sutherland)

[a]--Đoạn thẳng nằm hoàn toàn ngoài khi nó phạm bất kỳ một trong bốn bất đẳng thức sau: X1.X2 > Xmax; X1.X2 ‹ Xmin; Y1.Y2 > Ymax; Y1.Y2 ‹ Ymin;

[b]--Đoạn thẳng nằm hoàn toàn ngoài khi nó phạm bất kỳ một trong bốn bất đẳng thức sau: X1.X2 ≥ Xmax; X1.X2 ≤ Xmin; Y1.Y2 ≥ Ymax; Y1.Y2 ≤ Ymin;

[c]--Đoạn thẳng được hiển thị khi cả hai đầu cuối đều trong cửa sổ hiển thị

[d]--Đoạn thẳng được hiển thị khi: P1 mã or P2 mã =0000

14. Giải thuật LyangBarsky dựa vào phương trình đường thẳng: [a]--Không tường minh f(x,y) = 0

[b]--Do ông đưa ra

[c]--Tường minh y=f(x)

[d]--Tham số x = x(t), y = y(t) có t Є [0,1]

15. Cho cửa sổ cắt tỉa hình chữ nhật có góc trái dưới L(-2,-2), góc phải trên R(9,4). Cho đoạn CD có toạ độ là C(1,-3) và D(6,5), dùng giải thuật Lyangbarsky tính các giá trị P1 , P2 , P3và P4

[a]--P1 = -1, P2 = 1, P3 = 7 và P4 = -7

[b]--P1 = -6, P2 = 6, P3 = 8 và P4 = -8

[c]--P1 = -2, P2 = 2, P3 = 5 và P4 = -5 [d]--P1 = -5, P2 = - 5, P3 = 8 và P4 = -8

16. Dựa vào giải thuật LyangBarsky thì muốn tính giá trị mới u0 và u1 như sau : [a]--

[b]--

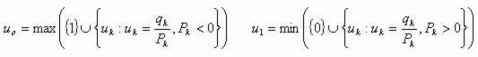
[c]--

[d]--

17. Trong giải thuật LyangBarsky thì để tính các giá trị trung gian q1 , q2 , q3 và q4 như sau:

[a]--q1=xmin - x1, q2=x1-xmax , q3=ymin - y1, q4=y1-ymax. [b]--q1=xmin - x1, q2=xmax-x1 , q3=ymin - y1, q4=ymax-y1.

[c]--q1=xmin - x1, q2=xmax-x1 , q3=y1 - ymin, q4=y1-ymax. [d]--Tất cả đều sai

18. Cho cửa sổ cắt tỉa hình chữ nhật có góc trái dưới L(-3,1), góc phải trên R(2,6). Dùng giải thuật Cohen Sutherland tìm hạng mục cắt tỉa của MN có M(-4,2) và N(-1,3).

[a]--(-4,2) và (-1,2)

[b]--(2, 3) và (-1,3)

[c]--(-3, 7/3) và (-1,3)

[d]--(-3,5) và (-1,3)

19. Cho cửa sổ cắt tỉa hình chữ nhật có góc trái dưới L(1,1), góc phải trên R(6,5). Dùng giải thuật Cohen Sutherland tìm hạng mục cắt tỉa của EF có E(2,2) và F(7,4).

[a]--(1,2) và (7,4)

[b]--(2, 2) và (6, 18/5)

[c]--(2, 3) và (-1,3)

[d]--(2, 2 ) và (1,18/5)

20. Hệ tọa độ thiết bị chuẩn (Normalized Devices coordinates) :

[a]--Một hình ảnh hiển thị được trên thiết bị này là chính xác thì chưa chắc hiển thị chính xác trên thiết bị khác

[b]--Một hình ảnh hiển thị được trên thiết bị này là chính xác thì chắc chắn sẽ hiển thị chính xác trên thiết bị khác

[c]--Một hình ảnh hiển thị được trên thiết bị này sẽ tạo ra hình ảnh tương tự trên thiết bị khác

[d]--Tất cả đều sai

Bài tập

1. Cho cửa sổ với các đường biên: xmin = 10, ymin = 47, xmax = 76, ymax = 165 và các đoạn thẳng:

+ Đoạn thẳng AB với điểm A(33, 210); điểm B(121, 187)

+ Đoạn thẳng CD với điểm C(-56, 173); điểm D(142, 2)

+ Đoạn thẳng EF với điểm E(76, 68); điểm F(19, 156)

Áp dụng giải thuật Liang-Barsky xác định chính xác phần nào trong các đoạn thẳng trên được hiển thị.

2. Cho cửa sổ với các đường biên: xmin = 10, ymin = 47, xmax = 76, ymax = 165 và tứ giác ABCD với điểm A(-33, 141); B(53, 145); C(45, 76); D(-25, 82). Áp dụng giải thuật Hodgman xác định chính xác phần nào của tứ giác ABCD được hiển thị.

3. Tìm ảnh của tam giác ABC với các toạ độ A(20,60), B(10,5), C(60,5) trong phép ánh xạ từ cửa sổ có các đường biên xwmin=ywmin= 20, xwmax=80, yvmax=60 vào khung nhìn có các đường biên xvmin = yvmin = 0, xvmax=yvmax =120

4. Cho cửa sổ với các đường biên: xmin = 40, ymin = 40, xmax = 180, ymax = 100 và các điểm A(93, 147); điểm B(121, 187); điểm C(77, 82); điểm D(136, 60); điểm E(93, - 20); điểm F(168, 160)

a. Áp dụng giải thuật Liang-Barsky xác định chính xác phần nào trong các đoạn thẳng AB, CD, EF được hiển thị.

b. Tìm ảnh của tam giác AEF trong phép ánh xạ từ cửa sổ vào khung nhìn với các đường biên xvmin = 10, yvmin = 20, xvmax= 290, yvmax =200.

5. Cho cửa sổ với các đường biên: xmin = 10, ymin = 20, xmax = 50, ymax = 80 và các điểm A(-30, 116); điểm B(90, 8); điểm C(0, 0); điểm D(5, 75); điểm E(50, 40); điểm F(82, 64)

a. Áp dụng giải thuật Cohen- Sutherland xác định chính xác phần nào trong các đoạn thẳng AB, CD, EF được hiển thị.

b. Tìm ảnh của tam giác ABC trong phép ánh xạ từ cửa sổ vào khung nhìn với các đường biên xvmin = 20, yvmin = 10, xvmax= 140, yvmax =130.

6. Cho cửa sổ với các đường biên: xmin = 20, ymin = 20, xmax = 80, ymax = 50 và các điểm A(-28, 92); điểm B(36, 92); điểm C(35, 16); điểm D(155, 4); điểm E(36, 36); điểm F(66, 41).

a. Áp dụng giải thuật Chia trung điểm xác định chính xác phần nào trong các đoạn thẳng AB, CD, EF được hiển thị.

b. Tìm ảnh của tam giác ABE trong phép ánh xạ từ cửa sổ vào khung nhìn với các đường biên xvmin = 20, yvmin = 10, xvmax= 140, yvmax =130.

7. Cho cửa sổ với các đường biên xmin= 55, xmax= 105, ymin = 35, ymax =85, và tam giác ABC với điểm A(27, 31); B(111, 112); C(200, 0).

a. Áp dụng giải thuật Hodgman xác định chính xác phần hiển thị của tam giác

ABC?

b. Tìm ảnh của tam giác ABC trong phép ánh xạ từ cửa sổ vào khung nhìn với

các đường biên xvmin = 0, yvmin = 10, xvmax= 100, yvmax = 110.

8. Cho cửa sổ với các đường biên xmin= 30, xmax=90, ymin = 70, ymax =130, và tứ giác ABCD với điểm A(30, 194); B(130, 34); C(90, 70); D(0, 0).

a. Áp dụng giải thuật Hodgman xác định chính xác phần hiển thị của tam giác ABCD?

b. Tìm ảnh của tứ giác ABCD trong phép ánh xạ từ cửa sổ vào khung nhìn với các đường biên xvmin = 30, yvmin = 70, xvmax= 90, yvmax = 130.

9. Cho cửa sổ với các đường biên xmin= 18, xmax=81, ymin = 115, ymax =147 và các đoạn thẳng:

+ Đoạn thẳng AB với điểm A(112, 190); điểm B(42, 39)

+ Đoạn thẳng CD với điểm C(48, 123); điểm D(169, 117)

+ Đoạn thẳng EF với điểm E(87, 67); điểm F(198, 48)

Áp dụng giải thuật Liang-Barsky xác định chính xác phần nào trong các đoạn thẳng trên được hiển thị.

10. Cho cửa sổ với các đường biên xmin= 18, xmax=100, ymin = 81, ymax =120 và các đoạn thẳng:

+ Đoạn thẳng AB với điểm A(6, 86); điểm B(72, 146)

+ Đoạn thẳng CD với điểm C(86, 101); điểm D(181, 107)

+ Đoạn thẳng EF với điểm E(35, 101); điểm F(72, 108)

Áp dụng giải thuật Cohen - Sutherland xác định chính xác phần nào trong các đoạn thẳng trên được hiển thị.

11. Cho cửa sổ với các đường biên xmin= 48, xmax=133, ymin = 64, ymax =149, và tứ giác ABCD với điểm A(15, 107); B(103, 125); C(170, 82); D(0, 0).

a. Áp dụng giải thuật Hodgman xác định chính xác phần hiển thị của tam giác ABCD?

b. Tìm ảnh của tứ giác ABCD trong phép ánh xạ từ cửa sổ vào khung nhìn với các đường biên xvmin = 30, yvmin = 70, xvmax= 90, yvmax = 130.

Hướng dẫn giải bài tập

1.

+ Xén tỉa đoạn thẳng AB: ta có:

p1 = -88, q1 = 23, p2 = 88, q2 = 43,p3 = 23, q3 = 163, p4 = -23, q4 = -45

u1 = 1.956522, u2 = 0.4886364

u1>u2 do đó kết luận đoạn thẳng AB nằm ngoài cửa sổ

+ Xén tỉa đoạn thẳng CD: ta có

p1 = -198, q1 = -66, p2 = 198, q2 = 132, p3 = 171, q3 = 126, p4 = -171,

q4 = -8

u1 = -66/-198, u2 = 132/198

Đoạn thẳng sau CD xén tỉa thành C‘D‘ với C‘(10, 116); D‘(76, 59)

+ Xén tỉa đoạn thẳng EF: ta có

p1 = 57, q1 = 66, p2 = -57, q2 = 0, p3 = -88, q3 = 21, p4 = 88, q4 = 97

u1 = 0, u2 = 1

Đoạn thẳng nằm trong cửa sổ

2. Xén tỉa đoạn thẳng AB với biến trái cửa sổ có giao điểm A‘(10, 143), điểm A nằm ngoài, B nằm trong lưu lại điểm A‘ và B. Xén tỉa đoạn thẳng BC có hai điểm B, C đều nằm trong cửa sổ lưu lại điểm C. Xén tỉa đoạn thẳng CD với biên trái có giao điểm D‘ (10, 79) có điểm C ở trong, điểm D ở ngoài, lưu điểm D. Xén tỉa đoạn thẳng DA với hai điểm A, D đều nằm ngoài do đó không lưu giữ điểm nào.Tứ giác ABCD được xén tỉa thành A‘BCD‘.

3. Xén tỉa đoạn thẳng AB với biên trái cửa sổ có giao điểm(20, 60) trùng điểm A với điểm A nằm trong cửa sổ, điểm B nằm ngoài, giữ lại điểm A. Xén tỉa đoạn thẳng BC với biên trái có giao điểm B‘(20, 50) với điểm B nằm ngoài, C nằm trong giữ lại điểm B‘ và C. Xén tỉa CD với cửa sổ có A, C đều nằm trong nên giữ lại điểm C, tam giác ABC được xén tỉa thành AB‘C.

Tính sx = 2 Tính sy = 3

Ánh xạ cửa sổ vào khung nhìn, áp dụng công thức ta có A(20, 6) trở thành A‘(0, 120). B‘(20, 50) trở thành B‘‘(0, 90). C(60, 50) trở thành C‘(89, 90).

4.

a.

+ Xén tỉa đoạn thẳng AB:

p1 = -28, q1 = 53, p2 = 28, q2 = 87, p3 = -40, q3 = 107, p4 = 40, q4 = -47 u1 = 0= 0/0, u2 = -1.175= -47/40

Do u1> u2 đoạn thẳng nằm ngoài cửa sổ

+ Xén tỉa đoạn thẳng CD

p1 = -59, q1 = 37, p2 = 59, q2 = 103, p3 = 22, q3 = 42, p4 = -22, q4 = 18 u1 = 0= 0/0

u2 = 1= 1/1

Đoạn thẳng nằm trong cửa sổ

+ Xén tỉa đoạn thẳng EF

p1 = -75, q1 = 53, p2 = 75, q2 = 87, p3 = -180, q3 = -60, p4 = 180, q4 = 120 u1 = -60/-180, u2 = 120/180

Đoạn thẳng sau khi xén tỉa: E‘ (118, 40)

F‘ (143, 100)

b.

Xén tỉa đoạn thẳng AE với cửa sổ, AE trở thành A‘(93, 100) E‘(93, 40)

Xén tỉa đoạn thẳng AF với cửa sổ ta có AF nằm ngoài cửa sổ. Tam giác AEF trở thành A‘HE‘F‘

Ánh xạ điểm A‘; H sang khung nhìn thành A‘‘(116, 200) H‘(116, 20) Ánh xạ điểm E‘; F‘ sang khung nhìn thành E‘‘(166, 20) F‘‘(216, 200)

5.

a. Đoạn thẳng AB với điểm A có mã 1001 điểm B có mã 0110, thực hiện xén tỉa AB với biên trái đoạn thẳng AB thành đoạn thẳng A‘B với A‘(10, 80) có mã 0000. Tiếp tục xén tỉa đoạn thẳng A‘B với biên phải ta được giao điểm B‘(50, 44) có mã 0000, kết thúc xén tỉa đoạn thẳng AB thành đoạn thẳng A‘B‘. Xén tỉa đoạn thẳng CD với điểm C có mã 0101 điểm D có mã 0001, hai điểm này có mã thứ nhất đều bằng 1 do đó đều nằm về phía trái của cửa số, kết thúc xén tỉa. Xén tỉa đoạn thẳng EF với điểm E có mã 0000, điểm F có mã 0010, thực hiện xén tỉa với biên phỉa ta được điểm F‘ (50, 40) có mã 0000 trùng điểm E, kết thúc

b. Xén tỉa tam giác ABC với biên trái ta được đa giác A‘BC‘ với điểm A‘(10, 80), điểm C nằm phía dưới cửa sổ. Xén tỉa A‘BC‘ với biên trên đa giác được giữ nguyên. Xén tỉa đa giác A‘BC‘ với biên phải ta được đa giác A‘B‘ D‘C‘ với điểm B‘(50, 44), D‘ nằm dưới cửa sổ. Xén tỉa A‘B‘D‘C‘ với biên dưới được đa giác A‘B‘D‘‘C‖, với D‘‘(50, 20) C‘‘(10, 20). Ánh xạ điểm A‘ qua khung nhìn thành A‘‘(20, 130).Ánh xạ điểm B‘ qua khung nhìn thành B‘‘(140, 58). Ánh xạ điểm D‘‘ qua khung nhìn thành D‘‘‘(140, 10).Ánh xạ điểm B‘ qua khung nhìn thành B‘‘(20, 10)

6.

a. Đoạn thẳng AE có điểm A với mã 1001, điểm E có mã 0000, gọi A1 trung điểm đoạn thẳng AE với A1(4, 64) có mã 1001, đoạn thẳng AE được rút ngắn thành A1E. Gọi A2 là trung điểm A1E với A2(4, 50) có mã 0000 đoạn thẳng A1E được xén tỉa thành A2E. Kết thúc. Đoạn thẳng CD có điểm C với mã 0100, điểm D với mã 0110, mã(C) and mã(D) ≠ 0000 nên đoạn thẳng CD nằm ngoài cửa sổ. Đoạn thẳng EF với điểm E có mã 0000, điểm F có mã 0000, do đó đoạn thẳng EF nằm hoàn toàn trong cửa sổ

b. Xén tỉa tam giác ABE với biên trái ta được tứ giác A‘B‘BE với điểm A‘(20,

50) B‘(20, 92). Xén tỉa ABE với biên bên trên ta được tam giác A‘CE với C(36, 50). Ánh xạ điểm A‘ qua khung nhìn thành A‘‘(20, 130). Ánh xạ điểm C qua khung nhìn thành C‘(53, 130). Ánh xạ điểm E qua khung nhìn thành E‘(52, 74)

7.

a. Xén tỉa tam giác ABC với biên trái, tam giác trở thành tứ giác A‘BCD với A(55, 58) D là điểm nằm dưới cửa sổ. Xén tỉa tứ giác A‘BCD với biên trên, đa giác A‘B‘ECD với điểm B‘(83, 85) điểm E nằm phía bên phải cửa sổ. Xén tỉa đa giác A‘B‘ECD với biên phải, đa giác A‘B‘ECD thành đa giác A‘B‘E‘C‘D với E‘(105, 85) C‘ nằm dưới cửa sổ. Xén tỉa đa giác A‘B‘E‘C‘D với biên dưới, đa giác trở thành A‘B‘E‘C‘D‘với điểm D‘(55, 35), C‘‘(105, 35). Kết thúc

b. Ánh xạ điểm A‘ qua khung nhìn thành A‘‘(0, 56), Ánh xạ điểm B‘ qua khung nhìn thành B‘‘(56, 110), Ánh xạ điểm E‘ qua khung nhìn thành E‘‘(100, 110), Ánh xạ điểm D‘ qua khung nhìn thành D‘‘(0, 10), Ánh xạ điểm C‘‘ qua khung nhìn thành C‘‘‘(100, 10)

8.

a. Xén tỉa tứ giác ABCD với biên trái thành tứ giác ABCD‘; với điểm D‘ nằm dưới cửa sổ. Xén tỉa đa giác với biên trên đa giác trở thành ngũ giác A‘BCD‘E với điểm A‘(70, 130), E (30, 130). Xén tỉa đa giác với biên bên phải đa giác trở thành A‘B‘CD‘E với B‘(90, 98). Xén tỉa đa giác với biên bên dưới đa giác trở thành A‘B‘CD‘‘E với D‘‘(30, 70)

b. Ánh xạ điểm A‘ thành A‘‘(0, 56), Ánh xạ điểm B‘ thành B‘‘(56, 110), Ánh xạ điểm C thành C‘(100, 110), Ánh xạ điểm D‘ thành D‘‘(100, 10), Ánh xạ điểm E thành E‘(0, 10)