Xây dựng theo phương pháp định nghĩa các ký tự bởi đường cong mềm bao ngoài của chúng dễ dàng thay đổi kích thước của ký tự cũng như nội suy ra các dạng của ký tự. Hoàn toàn độc lập với thiết bị.
+ Bitmap: Định nghĩa mỗi ký tự với 1 font chữ cho trước là 1 ảnh bitmap hình chữ nhật nhỏ. Biểu diễn ký tự bitmap có một số đặc điểm sau:
Đơn giản trong việc sinh ký tự ( copypixel) Lưu trữ lớn
Các phép biến đổi (I,B, scale) đòi hỏi lưu trữ thêm kích thước không đổi

Hình 2.19 Ký tự bitmap
Bitmap: Sử dụng hàm copypixel (copy điểm ảnh) được lưu trữ trong bộ nhớ cố định - Fontcache, đưa vào bộ nhớ đệm hiển thị. Mỗi 1 ký tự như 1 ma trận 2 chiều của các điểm ảnh - mặt nạ.
procedure Hàm_sinh_ki_tu (mask)
{
Có thể bạn quan tâm!
-
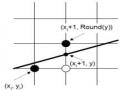
 Các Điểm X I 1 , Y I 1 Chọn Ở Bước (I+1) Cho Trường Hợp Đoạn Thẳng Có Hệ Số Góc 0
Các Điểm X I 1 , Y I 1 Chọn Ở Bước (I+1) Cho Trường Hợp Đoạn Thẳng Có Hệ Số Góc 0 -
 Các Vị Trí Đối Xứng Trên Đường Tròn (C) Tương Ứng Với (X,y)
Các Vị Trí Đối Xứng Trên Đường Tròn (C) Tương Ứng Với (X,y) -
 Mô Tả Giải Thuật Sinh Đường Ellipse
Mô Tả Giải Thuật Sinh Đường Ellipse -
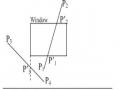
 A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ
A)Đối Tượng Cổng Xem; B)Đối Tượng Trong Cửa Sổ -
 Các Mã Vùng Nhị Phân Cho Các Điểm Đầu Mút Đoạn Thẳng Được Dùng Để Định Nghĩa Các Vùng Tọa Độ Liên Hệ Với Một Cửa Sổ.
Các Mã Vùng Nhị Phân Cho Các Điểm Đầu Mút Đoạn Thẳng Được Dùng Để Định Nghĩa Các Vùng Tọa Độ Liên Hệ Với Một Cửa Sổ. -
 Các Trường Hợp Xén Tỉa Một Cạnh Của Cửa Sổ Với Biên Cửa Sổ
Các Trường Hợp Xén Tỉa Một Cạnh Của Cửa Sổ Với Biên Cửa Sổ
Xem toàn bộ 240 trang tài liệu này.
xmax, ymax, xmin, ymin //các giới hạn của mặt nạ xo, yo//điểm gốc trên bộ đệm hiển thị
for i:= y min to ymax – 1 do for j:= xmin to xmax -1 do

if (mask(i,j) <> 0) then copypixel ((mask(i,j), pixel(xo+j, yo+i));
}
Ký tự fontcache bitmap đơn giản của SRG lưu trữ các ký tự theo chuỗi liên tiếp nhau trong bộ nhớ. Nhưng độ rộng các ký tự khác nhau, truy nhập các fontcache thông qua bản ghi về cấu trúc cho từng kí tự.
Cấu trúc font chữ
Charlocation =record leftx: integer;
width: integer;;
end;
fontcache =record CacheId: integer;
Height: integer; // Độ rộng chữ
CharSpace: integer; // Khoảng cách giữa các ký tự Table: array [0..127] of Charlocation;
end;
Bài tập áp dụng:
Bài toán: Vẽ đồ thị của hàm số y = f(x) trên đoạn [Min,Max].
Ý tưởng: Cho x chạy từ đầu đến cuối để lấy các tọa độ (x,f(x)) sau đó làm tròn thành số nguyên rồi nối các điểm đó lại với nhau.
Giải thuật:
Bước 1: Xác định đoạn cần vẽ [Min,Max].
Bước 2: - Đặt gốc tọa độ lên màn hình (x0,y0).
- Chia tỷ lệ vẽ trên màn hình theo hệ số k.
- Chọn bước tăng dx của mỗi điểm trên đoạn cần vẽ.
Bước 3: Chọn điểm đầu cần vẽ: x = Min, tính f(x) Đổi qua tọa độ màn hình và làm tròn:
x1:=x0 + Round(x.k); y1:=y0 - Round(y.k);
Di chuyển đến (x1,y1): MOVETO(x1,y1);
Bước 4:
Tăng x lên với số gia dx: x:=x + dx; Đổi qua tọa độ màn hình và làm tròn:
x2:=x0 + Round(x.k); y2:=y0 - Round(y.k);
Vẽ đến (x2,y2): LINETO(x2,y2);
Bước 5: Lặp lại bước 4 cho đến khi x > Max thì dừng. Ví dụ: Vẽ đồ thị hàm số f(x) = Sin(x)
Uses crt,Graph;
Var dau,cuoi:real;
Gd,Gm:Integer; Function F(x:real):real;
Begin
F:=Sin(x); End;
Procedure VeHinhSin(ChukyDau,ChuKyCuoi:real); var x1,y1,x2,y2:integer;
a,x,k:real; x0,y0:word;
Begin
x0:=GetMaxX div 2; y0:=GetMaxY div 2; K:=GetMaxX/30;
a:=Pi/180; x:=ChuKyDau;
x1:=x0 + Round(x*k); y1:=y0 - Round(F(x)*k); Moveto(x1,y1);
While x x:=x+a; x2:=x0 + Round(x*k); y2:=y0 - Round(F(x)*k); LineTo(x2,y2); End; End; BEGIN Gd:=0; InitGraph(Gd,Gm,’C:BPBGI’); Dau:=-4*Pi; cuoi:=4*Pi; VeHinhSin(Dau,cuoi); repeat until KeyPressed; CloseGraph; END. CÂU HỎI VÀ BÀI TẬP CHƯƠNG 2 Chọn một phương án đúng cho mỗi câu hỏi sau: 1. Xây dựng giải thuật tổng quát để vẽ đoạn thẳng ta có xét hệ số k (hệ số góc của đoạn thẳng) có tất cả các trường hợp của k: [a]--2 [b]--4 [c]--6 [d]--8 2. Để biểu diễn đoạn thẳng thông qua phương trình tham số như sau: [a]--f(x,y)=0 hay ax + by +c =0 [b]--x(v)=x1 +v(x2 -x1 ) và y(v) = y1 +v(y2 -y1 ) có v Є [0,1] [c]--P(u) = P1 + u(P2 -P1 ) có u Є [0,1] [d]--y=f(x) hay y=kx+b 3. Trong giải thuật Bresenham (vẽ đoạn thẳng) dùng biểu diễn đoạn thẳng là: [a]--Phương trình không tường minh [b]--Phương trình tường minh [c]--Phương trình các điểm gần với đoạn thẳng [d]--Phương trình tham số 4. Trong giải thuật Midpoint (vẽ đoạn thẳng) dùng biểu diễn đoạn thẳng là: [a]--Phương trình không tường minh [b]--Phương trình tường minh [c]--Phương trình điểm giữa [d]--Phương trình tham số 5. Giải thuật sau là giải thuật nào đã học? procedure Function(xt,yt,r,c:integer){ var x, y, d:integer; x := 0; y := r; d := 3 - 2 * r; while (x <= y) do begin putpixel(xt + x, yt + y, c); putpixel(xt - x, yt + y, c); putpixel(xt + x, yt - y, c); putpixel(xt - x, yt - y, c); putpixel(xt + y, yt + x, c); putpixel(xt - y, yt + x, c); putpixel(xt + y, yt - x, c); putpixel(xt - y, yt - x, c); if (d < 0) then d := d+ 4 * x + 6; else begin d := d+4 * (x-y) + 10; y := y -1; end; x:= x +1; end; end; [a]--Giải thuật Bresenham xây dựng đường tròn [b]--Giải thuật Midpoint xây dựng đường tròn [c]--Giải thuật Bresenham xây dựng đường Ellipse [d]--Giải thuật Midpoint xây dựng đường Ellipse 6. Giải thuật sau là giải thuật nào đã học? procedure Function(xt, yt, r, c:integer){ var x, y, d:integer; x := 0; y := r; d := 1 - r; while (x <= y) do begin putpixel(xt + x, yt + y, c); putpixel(xt - x, yt + y, c); putpixel(xt + x, yt - y, c); putpixel(xt - x, yt - y, c); putpixel(xt + y, yt + x, c); putpixel(xt - y, yt + x, c); putpixel(xt + y, yt - x, c); putpixel(xt - y, yt - x, c); if (d < 0) then d :=d+ 2 * x + 3; else begin d :=d+ 2* (x-y) + 5; y:=y-1; end; x:=x+1; end; end; [a]--Giải thuật Bresenham xây dựng đường tròn [b]--Giải thuật Midpoint xây dựng đường Ellipse [c]--Giải thuật Midpoint xây dựng đường tròn [d]--Giải thuật Bresenham xây dựng đường Ellipse 7. Điểm đầu nút của đoạn thẳng (-2,6) và (6,18), tính giá trị của k: [a]--k= 3 [b]--k= -6 [c]--k= 1.5 [d]--k= -3 8. Đoạn mã sau là thuộc giải thuật Bresenham vẽ đoạn thẳng: dx:=x2-x1; dy:=y2-y1; for x:=x1 to x2 do begin putpixel(x,y,c); if(p<0) then p :=p+ 2*dy; else begin p :=p+ 2*dy - 2*dx; y:=y+1; end; end; [a]--Đúng [b]—Sai 9. Điểm đầu nút của đoạn thẳng (-2,-6) và (3,-2), tính giá trị của k : [a]--k= -0.8 [b]--k= 3 [c]--k= 0.8 [d]--k= 1.5 10. Giải thuật sau là giải thuật nào? procedure ThuTuc(X[],Y[]) begin for i:=0 to 6 do line(X[i],Y[i],X[i+1],Y[i+1]); line(X[i+1],Y[i+1],X[0],Y[0]); end; [a]--Giải thuật vẽ đường bao đa giác với số đỉnh là 8 [b]--Giải thuật tô đa giác với số đỉnh là 7 [c]--Giải thuật vẽ đường bao đa giác với số đỉnh là 7 [d]--Giải thuật vẽ đường bao đa giác với số đỉnh là 6 11. Giải thuật sau là giải thuật nào? procedure ThuTuc( X[], Y[]) begin for i:=0 to 5 do line(X[i],Y[i],X[i+1],Y[i+1]); line(X[i+1],Y[i+1],X[0], Y[0]); end; [a]--Giải thuật vẽ đường bao đa giác với số đỉnh là 7 [b]--Giải thuật vẽ đường bao đa giác với số đỉnh là 5 [c]--Giải thuật tô đa giác với số đỉnh là 6 [d]--Giải thuật vẽ đường bao đa giác với số đỉnh là 6 12. Phương trình không tường minh cho đường tròn là: (r là bán kính của đường tròn) [a]--f(x,y)=x2 +y2 -r2 =0 [b]--f(x +1,y -1/2)=0 [c]--(x-1)2 + (y-1)2 = (r-1)2 [d]--f(x,y)=b2x2 + a2y2 - a2b2 =0 13. Phương trình không tường minh cho đường Ellipse là: (ra là bán kính theo trục ox, rb là bán kính theo trục oy và (xc,yc) là tọa độ tâm): [a]--f(x,y) = rb2(xc+x)2 + ra2(yc+y)2 - ra2rb2 = 0 [b]--f(x,y)=(xc+x)2/ra2 + (yc+y)2/rb2 - ra2rb2 =0 [c]--f(x i +1,y i -1/2) = 0 [d]--ra2(xc+x)2 + rb2(yc+y)2 - ra2rb22=0 14. Theo giải thuật Midpoint vẽ đoạn thẳng thì d i = f(x i +1,y i +1/2) - trung điểm, với giá trị nào của d để trung điểm nằm dưới đoạn thẳng: [a]--di = 0 [b]--di = di+1 [c]--di > 0 [d]--di < 0 15. Đoạn thẳng có 2 điểm cuối là (1,1) và (8,5). Dùng thuật toán Bresenham vẽ đoạn thẳng tính các giá trị tại x=3. [a]--p=5 và y=3 [b]--p=2 và y=4 [c]--p=-3 và y= 2 [d]--p=-3 và y= 3 16. Đoạn thẳng có 2 điểm cuối là (1,1) và (8,5). Dùng thuật toán Midpoint vẽ đoạn thẳng tính các giá trị tại x=3. [a]--d=4 và y=3 [b]--d=-3 va y=3 [c]--d=-2 và y=2 [d]--d=2 và y=2 Bài tập 1. Tính các điểm được vẽ trên các đoạn thẳng giới hạn bởi các cặp điểm sau: a. A(10, 20), B(18, 27) theo thuật toán DDA b. C(16,19), D(24, 25) theo thuật toán Bresenham C. E(15, 17), F(23, 22) theo thuật toán Midpoint 2. Tính các điểm được vẽ trên các đường tròn sau: a. Đường tròn có phương trình (x – 6)2 + (y-3)2 = 121 theo thuật toán Midpoint b. Đường tròn có bán kính bằng 10 và tâm tại điểm (5, 5) theo thuật toán Bresenham 3. Trình bày giải thuật DDA sinh đường thẳng với hệ số góc m > 1, Dx >0. Áp dụng giải thuật, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm với các tọa độ A(15, 27), B(22, 35). 4. Trình bày giải thuật Midpoint sinh đường thẳng với hệ số góc m > 1, Dx >0. Áp dụng giải thuật, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(12, 19); B(18, 27). 5. Trình bày giải thuật Bresenham sinh đường thẳng với hệ số góc m > 1, Dx >0. Áp dụng giải thuật, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(20, 22); B(25, 30). 6. Áp dụng giải thuật Bresenham viết hàm sinh đoạn thẳng (xét tất cả các trường hợp của hệ số góc). 7. Áp dụng giải thuật Midpoint viết hàm sinh đoạn thẳng (xét tất cả các trường hợp của hệ số góc). 8. Áp dụng giải thuật DDA viết hàm sinh đoạn thẳng (xét tất cả các trường hợp của hệ số góc).