Để đơn giản hóa quá trình xây dựng giải thuật, ta xét các đường thẳng có hệ số góc dương và nhỏ hơn 1 để đảm bảo bộ biến thiên theo trục x lớn hơn độ biến thiên theo trục y. Khi đó cho x biến thiên mỗi lần một pixel và độ biến thiên của y được tính theo x.
Giả sử xi, yi
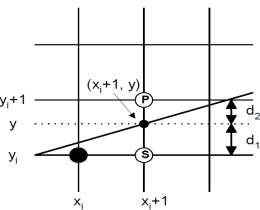
là điểm đã xác định được ở bước thứ i (điểm màu đen) thì điểm
cần chọn xi1, yi1 ở bước thứ (i+1) sẽ là một trong hai trường hợp (điểm màu trắng) như hình vẽ sau:
2
yi1
(xi+1, yi+1) (xi+1, yi)
xi
Hình 2.9 Các điểm xi1 , yi1 chọn ở bước (i+1) cho trường hợp đoạn thẳng có hệ số góc 0
xi1 xi 1
Như vậy :
y
yi
y
i1
i1
Vấn đề còn lại là cách chọn một trong hai điểm trên như thế nào để có thể tối ưu về mặt tốc độ.
2.3.2 Thuật toán DDA (Digital Differential Analyzer)
Với thuật toán DDA, việc quyết định chọn
yi1 là
yi hay yi 1, dựa vào
phương trình của đoạn thẳng y = mx +b. Nghĩa là, ta sẽ tính tọa độ của điểm xi1, y
thuộc về đoạn thẳng thực. Tiếp đó, yi+1sẽ là giá trị sau khi làm tròn giá trị tung độ y.
Như vậy: ymxi1b
y
i1
Round y
Nếu tính trực tiếp giá trị thực y ở mỗi bước từ phương trìnhy = mx + b thì phải cần một phép toán nhân và một phép toán cộng số thực. Để cải thiện tốc độ, người ta tính giá trị thực của y ở mỗi bước theo cách sau để khử phép tính nhân trên số thực:
Nhận xét yi1 mxi1 b mxi1 b = mxi+ b + m mà yi= mxi+ b
Do đó: yi+1 = yi + m
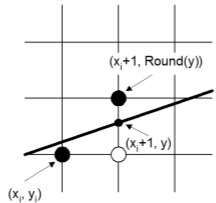
Hình 2.10 Minh họa thuật toán DDA
Thuật toán này do cách làm tròn tọa độ thực ở những bước tính toán cuối cùng nên độ chính xác của giải thuật cao, đường thẳng vẽ được thể hiện gần với đường thẳng thực tế. Tuy nhiên cũng vì vậy mà tốc độ tính toán chậm do phải làm việc thường xuyên trên số thực và các phép toán phức tạp nên thuật toán ít được sử dụng.
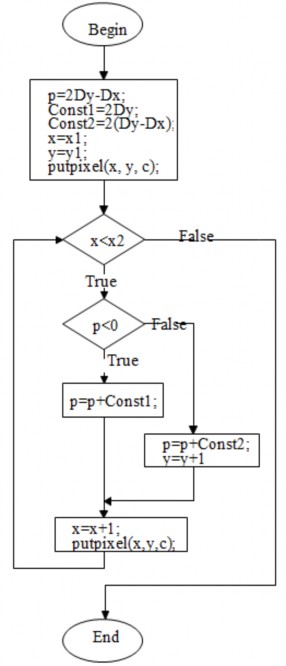
Lưu đồ thuật toán và chương trình cài đặt thuật toán DDA vẽ đường thẳng
procedure LineDDA (x1, y1, x2, y2, color :integer) begin
var x,i:integer; y, m: real;
x := x1;
y := y1;
m := (y2-y1)/(x2-x1); putpixel(x, Round(y), Color); for i:=x1 to x2 -1 do
begin
end; end;
x := x +1;
y :=y + m;
putpixel(x, Round(y), Color);
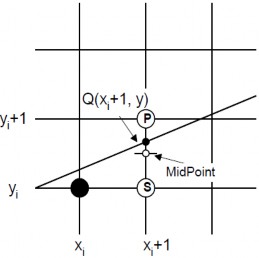
x No Yes End x=x+1; y=y+m; putpixel(x, Round(y),c); Begin m=Dy/Dx; x=x1; y=y1; putpixel(x, Round(y), c); Ví dụ 2.1. Áp dụng giải thuật DDA, tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(12, 20) và B(22, 27) Ta có Dx = 22-12=10; Dy = 27-20=7; m = 0.7 Bước xi yi y 0 12 20 20 1 13 21 20.7 2 14 21 21.4 3 15 22 22.1 4 16 23 22.8 5 17 24 23.5 Có thể bạn quan tâm! Xem toàn bộ 240 trang tài liệu này. 6 18 24 24.2 7 19 25 24.9 8 20 26 25.6 9 21 26 26.3 10 22 27 27 Nhận xét Việc sử dụng công thức yi+1 = yi + m để tính giá trị y tại mỗi bước đã giúp cho thuật toán DDA nhanh hơn hẳn so với cách tính y từ phương trình y= mx +b do khử được phép nhân trên số thực. Tuy nhiên, việc cộng dồn giá trị thực m vào y có thể sẽ tích lũy sai số làm cho hàm làm tròn có kết quả sai dẫn tới việc xác định vị trí của điểm vẽ ra bị chệch hướng so với đường thẳng thực. Điều này chỉ xảy ra khi vẽ đoạn thẳng khá dài. Tuy đã khử được phép nhân số thực nhưng thuật toán DDA vẫn còn bị hạn chế về mặt tốc độ do vẫn còn phép toán cộng số thực và làm tròn. Có thể khắc phục thao tác cộng số thực m và làm tròn trong thuật toán bằng cách nhận xét là các số nguyên. 2.3.3 Giảithuật Bresenham m Dy với Dy, Dx Dx Thuật toán Bresenham đưa ra cách chọn yi+1 là yi hay yi +1theo một hướng khác sao cho có thể tối ưu hóa về mặt tốc độ so với thuật toán DDA. Vấn đề mấu chốt ở đây là làm thế nào để hạn chế tối đa các phép toán trên số thực trong thuật toán. Ý tưởng của thuật toán Bresenham được trình bày như sau : Hình 2.11 Minh họa thuật toán Bresenham i Gọi x 1, ylà điểm thuộc đoạn thẳng. Ta có: y mx 1 b . i d1 y yi Đặt d2 yi 1 y Xét tất cả các vị trí tương đối của y so với yi và yi 1, việc chọn điểm i1 i1 1 2 x , y là S hay P phụ thuộc vào việc so sánh d1 và d2 hay dấu của d d Nếu d1 d2 0 , chọn điểm S, tức là yi1 yi . Ngược lại, nếu d1 d2 0 , chọn điểm P, tức là yi 1 yi 1. Xét pi Dxd1 d2 Dx2y 2yi1 pi Dx2mxi1 b 2yi1 Thay m Dy Dx vào phương trình trên ta được: pi 2Dyxi 2Dxy i c , với c 2Dy 2b 1Dx . Nhận xét: do Dx 0 nên dấu của biểu thức d1 d2 cũng chính là dấu của pi. Hay nói một cách khác, nếu tại bước thứ i đã xác định được dấu của xác định được điểm cần chọn ở bước (i+1). pi thì xem như Tính được pi tại mỗi bước: Ta có: pi1 pi2Dyxi1 2Dxy i1 c2Dyxi 2Dxy i c pi1 pi 2Dyxi1 xi 2Dxyi1 yi pi1 pi 2Dy 2Dxyi1 yi, do xi1 xi 1 Từ đây có thể suy ra cách tính pi1 từ pi như sau: - Nếu pi 0 thì pi1 pi 2Dy do chọn yi 1 yi . - Ngược lại, nếu pi 0 , thì pi1 pi 2Dy 2Dx , do chọn yi1 yi 1. Giá trị p0 được tính từ điểm vẽ đầu tiên x0, y0theo công thức: p0 2Dyx0 2Dxy 0 c 2Dyx0 2Dxy 0 2Dy 2b 1Dx 0 0 Do x , y là điểm nguyên thuộc về đoạn thẳng nên ta có: y0 mx 0 b Dy x Dx 0 b . thẳng Thế vào phương trình trên ta tính được: p0 2Dy Dx . Lưu đồ thuật toán và chương trình cài đặt thuật toán Bresenham vẽ đường procedure LineBres (x1, y1, x2, y2, color:integer) begin var Dx, Dy, p, Const1, Const2, i : integer; x, y:integer; Dx := x2 - x1; Dy := y2 - y1; p := 2*Dy - Dx; Const1 := 2*Dy; Const2 := 2*(Dy-Dx); x := x1; y := y1; putpixel(x, y, Color); for i:=x1 to x2 do begin if (p<0) then p := p + Const1 else begin p := p + Const2; y := y + 1; end; end; end; x:= x +1; putpixel(x, y, Color); Ví dụ 2.2.Tính các điểm được vẽ trên đoạn thẳng giới hạn bởi 2 điểm A(12, 20), B(22, 27). Ta có: Dx = 22 -12 =10, Dy = 27 – 20 = 7 Const1 = 2Dy = 14, Const2 = 2(Dy - Dx) = -6 P0 = 2Dy – Dx = 14 – 10 = 4 Ta có bảng xác định các điểm vẽ nguyên của đoạn thẳng AB như sau: Bước xi yi p 0 12 20 4 1 13 21 -2 2 14 21 12 3 15 22 6 4 16 23 0 5 17 24 -6 6 18 24 8 7 19 25 2 8 20 26 -4 9 21 26 10 10 22 27 4 Nhận xét Thuật toán Bresenham chỉ làm việc trên số nguyên và các thao tác trên số nguyên chỉ là phép cộng và phép dịch bit (phép nhân 2) điều này là một cải tiến làm tăng tốc độ đáng kể so với thuật toán DDA. Ý tưởng chính của thuật toán nằm ở chỗ xét dấu pi để quyết định điểm kế tiếp, và sử dụng công thức truy hồi pi+1 - pi để tính pi bằng các phép toán đơn giản trên số nguyên. Thuật toán này cho kết quả tương tự như thuật toán DDA. 2.3.4 Thuật toán MidPoint Thuật toán MidPoint đưa ra cách chọn yi+1 là yi hay yi +1 bằng cách so sánh điểm thực Q(xi + 1, y) với điểm MidPoint là trung điểm của S và P (hình 2.11). Ta có: Nếu điểm Q nằm dưới điểm MidPoint, ta chọn S. Ngược lại nếu điểm Q nằm trên điểm MidPoint ta chọn P. Hình 2.12 Minh họa thuật toán MidPoint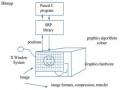
Đồ họa máy tính - 2
Các Thành Phần Phần Cứng Của Hệ Tọa Độ Tương Tác
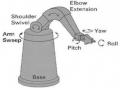Ảnh Cánh Tay Robot Được Cấu Tạotừ Các Đối Tượng Đồ Họa Cơ Sở
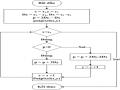Các Vị Trí Đối Xứng Trên Đường Tròn (C) Tương Ứng Với (X,y)
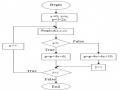Mô Tả Giải Thuật Sinh Đường Ellipse
Đồ họa máy tính - 8
