Dao động kỹ thuật - 22

Nếu dầm đặt trên nền đàn hồi tuyến tính với hệ số cứng k và chịu tác dụng của lực dọc trục thì phương trình dao động uốn của dầm có dạng

2w

2 

2w

w

(x) t2

x2EI (x) x2x N (x, t) x kw  0

(3.104)



b. Dao động uốn tương đối của dầm gắn trên đĩa quay

Bây giờ ta chuyển sang xét bài toán dao động uốn tương đối của dầm quay đều. Đây là lớp bài toán hay gặp trong thực tế. Dao động uốn của cánh tua bin, dao động uốn của các cánh rôto của máy bay trực thăng. Ký hiệu chiều dài dầm là l, độ cứng chống uốn EI = const, khối lượng đơn vị dài của dầm  = A = const. Xét dao động uốn tương đối trong mặt phẳng vuông góc với trục quay. Trục rôto quay đều với vận tốc góc . Giả thiết biến dạng góc nhỏ w’(x,t) << 1. Do đó có thể bỏ qua ảnh hưởng của lực quán tính Coriolis, chỉ quan tâm đến ảnh hưởng của lực quán tính theo (lực ly tâm). Xét mô hình dao động như hình 4.25.

Áp dụng nguyên lý d’Alembert, từ điều kiện cân bằng các lực theo trục z ta có:

2w

Q 

dx t2

Fz Q cos (Q x dx) cos(x dx)

N sin  (N N dx) sin(dx)  0

(3.105)

x x

Lực quán tính ly tâm của phần tử dầm dx là F(x) = dxr(x)2. Từ đó suy ra (hình 4.25a)

Fz(x) = F(x)sin = 2wdx (3.106)

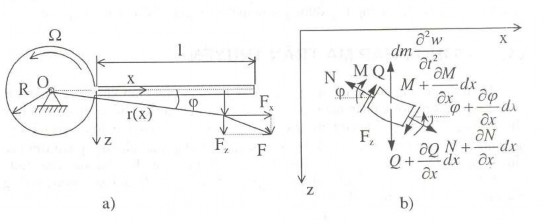
Hình 4.25 Dầm gắn trên đĩa quay

Thế biểu thức (3.106) vào (3.105) và thay thế cos 1,

cos(dx)  1,

x

sin, sin(dx) dx

x x

ta được

2w 

4w 

w2 

(3.107)

t2

EI x4

x N (x, t) x w 0

Lực pháp tuyến N(x,t) có thể tính theo đoạn dầm từ mặt cắt x đến mặt cắt l.

1

N (x, t) (R x)2dx 

0

1 2 (1x)(2R 1x)

2

(3.108)

Thế (3.108) vào (3.107) ta nhận được phương trình vi phân dao động uốn tương đối của dầm quay đều.

2w 

4w 2 1 

w

t2

EI x4

2 x (1

x)(2R 1

x) x 

w 0

(3.109)



Việc giải các phương trình vi phân dao động uốn của dầm chịu tác dụng của lực dọc trục và phương trình vi phân dao động uốn tương đối của dầm gắn trên đĩa quay đều được xét một cách chi tiết trong cuốn Bài tập dao động kỹ thuật [12]. Trong đó ta thấy các tần số riêng của dầm quay đều lớn hơn so với tần số riêng của dầm không quay. Hiệu ứng này được gọi là hiệu ứng gia cố độ cứng động lực.

CÂU HỎI ÔN TẬP

1. Thiết lập phương trình tần số của thanh đồng chất có tiết diện không đổi có đầu trái ngàm, đầu phải chịu liên kết với lò xo cos độ cứng c0 như hình 4.26. Xác định hai tần số riêng đầu tiên nếu c0 = EA / l.

Có thể bạn quan tâm!

• Dao Động Uốn Tự Do Của Dầm Euler- Bernoulli Đồng Chất Tiết Diện Không Đổi
• Các Phương Trình Đặc Trưng Và Các Trị Riêng Của Một Số Dầm
• Dao động kỹ thuật - 21

Xem toàn bộ 182 trang tài liệu này.

x

c0

Hình 4.26 Hình bài tập 1

2. Đầu trái của thanh đồng chất có tiết diện không đổi gắn với một lò xo có độ cứng k, đầu kia tự do (Hình 4.27).

a. Viết phương trình xác định tần số dao động

x

b. Xác định hai tần số đầu của thanh biết k = EA /l. k u

Hình 4.27 Hình bài tập 2

3. Cả 2 đầu thanh đều gắn lò xo như hình 4.28. Lập phương trình xác định tần số dao động của thanh. Tính hai tần số riêng đầu tiên khi k1 = 2k2 = EA/l.

k1

E, A, l

k2

x

Hình 4.28 Hình bài tập 3

4. Một thanh đồng chất chuyển động dọc theo trục x với vận tộc v không đổi (hình 4.29). Thanh bị va chạm vào một vật chắn, rắn tuyệt đối sao cho từ đó trửo đi mút trái của thanh luôn luôn gắn cứng vào vật rắn. Tính giá trị dịch chuyển cực đại ở đầu phải của thanh và giá trị ứng lực dọc cực đại ở đầu trái của thanh.

v

E, A, l

x

Hình 4.29 Hình bài tập 4

5. Cho biết thanh bị kéo bởi một lực P không đổi và ở một thời điểm nhất định, lực được bỏ đi đột ngột (hình 4.30). Tìm quy luật dịch chuyển của đầu mút phải của thanh.

E, A, l

P

u0

Hình 4.30 Hình bài tập 5

x

6. Hãy xác định hàm riêng của dao động dọc của thanh đồng chất có chiêu dài l mang khối lượng m ở một đầu còn đầu kia tự do.

E, A, l m

x

Hình 4.31 Hình bài tập 6

7. Tính các tần số riêng và hàm riêng của dao động xoắn của trục được cho trên hình a, b, c. Trục có tiết diện tròn, mật độ  và môđun cắt vật liệu G.

l

a)

l/2

b)

c)

Hình 4.32 Hình bài tập 7

	l

8. Xác định tần số dao động riêng của trục có tiết diện ngang tròn mang 2 đĩa ở đầu (hình 4.33). Cho biết mômen quán tính của đĩa bằng J1, J2 trục có mật độ khối  và mômen quán tính cực của tiết diện Ip.

J1 J2

Hình 4.33 Hình bài tập 8

9. Xác định dao động dọc cưỡng bức của thanh một đầu ngàm chặt, ở đầu kia chịu tác dụng của lực F(t) = F0sin(t) (hình 4.34).

10. Một thanh có một đầu tự do, một đầu chịu kích động động học theo luật u=u0sin(t) như hình 4.35. Xác định dao động dọc bình ổn của thanh.

11. Một thanh có đầu dưới mang khối lượng m, đầu trên dịch chuyển theo phương

thẳng đứng với luật u0 = Usint. Hãy tìm dao động dọc bình ổn của thanh và biên độ dao động dọc của khối lượng m (hình 4.36).

u0(t)

A,E

l

m

u0sint

x

x

F0sint Hình 4.34

Hình 4.35

Hình 4.36

12. Thiết lập phương trình vi phân uốn tự do của dầm và xác định các tần số riêng đối với các mô hình trên hình 4.37. Cho biết dầm đồng chất có tiết diện không đổi, độ cứng chống uốn EI, khối lượng đơn vị dài là μ .

a c

b d

Hình 4.37 Hình bài tập 12

13. Thiết lập phương trình dao động tự do của dầm đàn hồi năm trên nền đàn hồi (hình 4.38). Biết rằng phản lực của nền tác dụng lên mỗi đơn vị chiều dài của dầm tỷ lệ bậc nhất với độ vòng của dầm là kw (k là hệ số độ cứng của nền). Hãy tìm tần số riêng cho hai trường hợp sau:

x

x

w

a) b)

Hình 4.38 Hình bài tập 13

TÀI LIỆU THAM KHẢO

[1] Nguyễn Văn Khang, Dao động kỹ thuật, NXB Khoa học và Kỹ thuật, Hà Nội 2009

[2] Trần Doãn Tiến. Cơ sở dao động trong kỹ thuật, NXB Đại học và THCN, Hà Nội 1981.

[3]Phan Nguyên Di, Nguyễn Văn Khang, Tính toán dao động máy, NXB Khoa học và Kỹ thuật, Hà Nội 1991.

[4] Nguyễn Xuân Hùng, Tính toán chính xác kết cấu trên máy tính, NXB Khoa học và Kỹ thuật, Hà Nội 2002.

[5] Nguyễn Văn Khang, Cơ sở Cơ học kỹ thuật, Tập I và tập II, NXB Đại học quốc gia, Hà Nội 2003

[6] Lê Quang Minh, Nguyễn Văn Vượng, Sức bền vật liệu, NXB Giáo dục, Hà Nội 2004.

[7] Lê Ngọc Hồng, Sức bền vật liệu, NXB Khoa học kỹ thuật 2002.

[8] Bùi Trọng Lựu, Sức bền vật liệu tập 1, NXB Đại học và Trung học chuyên nghiệp, 2004.

[9] Bùi Trọng Lựu, Sức bền vật liệu tập 2, NXB Đại học và Trung học chuyên nghiệp, 2004.

[10] Bùi Trọng Lựu, Nguyễn Văn Vượng, Bài tập Sức bền vật liệu, NXB Giáo dục 2004.

[11] Đỗ Sanh, Nguyễn Văn Khang. Cơ học tập 2. NXB Giáo dục 2004.

[12] Nguyễn Văn Khang, Thái Mạnh Cầu, Vũ Văn Khiêm, Nguyễn Nhật Lệ, Bài tập dao động kỹ thuật, NXB Khoa học và Kỹ thuật, Hà Nội 2009.