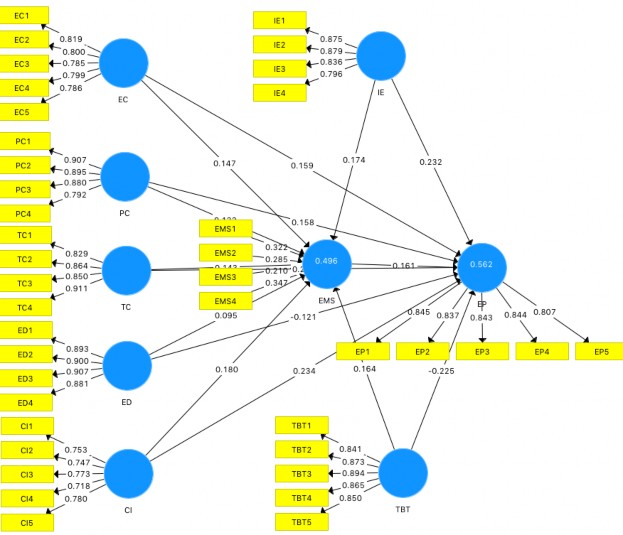
Hình 4.2: Mô hình đo lường chính thức
(Nguồn: Kết quả xử lý dữ liệu của tác giả) Kết quả bảng 4.3 cho thấy các thang đo có giá trị độ tin cậy tổng hợp (CR) >
0,7 (Giá trị CR thấp nhất là 0,868 và giá trị CR cao nhất là 0,942), chứng tỏ cả 8 đều có độ tin cậy nhất quán nội tại cao. Thêm nữa, hệ số Cronbach’s Alpha > 0,7 cho tất cả các biến. Chỉ số Cronbach’s Alpha thấp nhất là 0,811 và chỉ số Cronbach’s Alpha cao nhất là 0,918 cho thấy các thang đo có độ tin cậy tổng hợp cao.
Để đánh giá giá trị hội tụ sẽ dựa trên giá trị AVE, AVE của thang đo PC là 0,756; TBT là 0,748; TC là 0,746; IE là 0,718; kết quả xuất khẩu là 0,698; ED là 0,801; EC là 0,637; CI là 0,569 (Bảng 4.3) tất cả đều lớn hơn mức tối thiểu là 0,5. Vì vậy, cả 8 biến nghiên cứu này đều có độ hội tụ cao.
Bảng 4.3: Kết quả đánh giá độ tin cậy và giá trị hội tụ
(AVE) | ||||||
PC | PC1 | 0,892 | 0,898 | 0,925 | 0,907 | 0,756 |
PC2 | 0,895 | |||||
PC3 | 0,880 | |||||
PC4 | 0,792 | |||||
TBT | TBT1 | 0,916 | 0,923 | 0,937 | 0,841 | 0,748 |
TBT2 | 0,873 | |||||
TBT3 | 0,894 | |||||
TBT4 | 0,865 | |||||
TBT5 | 0,850 | |||||
TC | TC1 | 0,886 | 0,889 | 0,922 | 0,829 | 0,746 |
TC2 | 0,864 | |||||
TC3 | 0,850 | |||||
TC4 | 0,911 | |||||
IE | IE1 | 0,869 | 0,870 | 0,911 | 0,875 | 0,718 |
IE2 | 0,879 | |||||
IE3 | 0,836 | |||||
IE4 | 0,796 | |||||
EP | EP1 | 0,892 | 0,894 | 0,920 | 0,845 | 0,698 |
EP2 | 0,837 | |||||
EP3 | 0,843 | |||||
EP4 | 0,844 | |||||
EP5 | 0,807 | |||||
ED | ED1 | 0,918 | 0,924 | 0,942 | 0,893 | 0,801 |
ED2 | 0,900 | |||||
Có thể bạn quan tâm!
-
Kết Quả Hiệu Chỉnh Thang Đo Nghiên Cứu Định Tính Giai Đoạn 2 -
Kết Quả Phân Tích Độ Tin Cậy Của Các Thang Đo Sơ Bộ -
Kết Quả Phân Tích Phần Dư Của Thang Đo Nguyên Nhân -
Ước Lượng Hệ Số Đường Dẫn Và Khoảng Tin Cậy -
Kết Quả Đa Nhóm Kiểm Định Hoán Vị Số Năm Kinh Nghiệm Xuất Khẩu -
Vai Trò Trung Gian Của Chiến Lược Marketing Xuất Khẩu Thích Nghi
Xem toàn bộ 260 trang tài liệu này.
Thang đo
Biến quan sát
Cronbach's Alpha
rho_A
Độ tin cậy tổng hợp (CR)
Hệ số tải
Phương sai trích
trung bình
ED3 | 0,907 | |||||
ED4 | 0,881 | |||||
EC | EC1 | 0,858 | 0,860 | 0,898 | 0,819 | 0,637 |
EC2 | 0,800 | |||||
EC3 | 0,785 | |||||
EC4 | 0,799 | |||||
EC5 | 0,786 | |||||
CI | CI1 | 0,811 | 0,814 | 0,868 | 0,753 | 0,569 |
CI2 | 0,747 | |||||
CI3 | 0,773 | |||||
CI4 | 0,718 | |||||
CI5 | 0,780 |
(Nguồn: Kết quả xử lý dữ liệu của tác giả)
Sau đây, mô hình đo lường sẽ kiểm tra giá trị phân biệt của các biến nghiên cứu. Theo tiêu chí Fornell – Larcker, căn bậc hai của AVE cho từng biến nghiên cứu nên lớn hơn giá trị tương quan cao nhất của biến nghiên cứu này với biến nghiên cứu khác trong mô hình (so sánh AVE với bình phương tương quan giữa các biến nghiên cứu). Bảng 4.4 minh họa hệ số ma trận Fornell – Larcker cho thấy các hệ số trên cùng (in đậm) đều lớn hơn các hệ số trong cùng 1 cột. Tóm lại, các thang đo đều đạt giá trị phân biệt vì các chỉ số tính toán căn bậc hai của AVE đều cao hơn tương quan của các biến nghiên cứu với các biến tiềm ẩn của mô hình.
Một tiêu chí khác được dùng để kiểm tra giá trị phân biệt là thông qua hệ số tải chéo (Cross loadings). Giá trị phân biệt được tạo ra khi hệ số tải của biến quan sát lên biến nghiên cứu cao hơn tất cả hệ số tải chéo của nó lên các biến nghiên cứu khác. Ví dụ, biến CI1 có hệ số tải lớn nhất (0,753) khi đo lường biến CI (Bảng 4, Phụ lục 3), trong khi đó, tất cả các hệ số tải chéo với các biến khác thì tương đối thấp, tương tự cho các biến còn lại. Tóm lại, đánh giá theo tiêu chí hệ số tải chéo cung cấp bằng chứng về giá trị phân biệt của tất cả các biến nghiên cứu trong mô hình.
Bảng 4.4: Kiểm định giá trị phân biệt (Fornell – Larcker)
CI | EC | ED | EMS | EP | IE | PC | TBT | TC | |
CI | 0,754 | ||||||||
EC | 0,414 | 0,798 | |||||||
ED | 0,172 | 0,131 | 0,895 | ||||||
EMS | 0,517 | 0,501 | 0,267 | ||||||
EP | 0,543 | 0,480 | -0,005 | 0,520 | 0,835 | ||||
IE | 0,469 | 0,419 | 0,122 | 0,524 | 0,557 | 0,847 | |||
PC | 0,374 | 0,470 | 0,151 | 0,453 | 0,470 | 0,419 | 0,870 | ||
TBT | 0,400 | 0,458 | 0,348 | 0,511 | 0,224 | 0,429 | 0,324 | 0,865 | |
TC | 0,443 | 0,393 | 0,163 | 0,483 | 0,524 | 0,469 | 0,304 | 0,398 | 0,864 |
(Nguồn: Kết quả xử lý dữ liệu của tác giả)
Cuối cùng, phương pháp HTMT được nhận xét là lựa chọn tin cậy hơn để đánh giá giá trị phân biệt so với tiêu chí Fornell – Larcker và hệ số tải chéo. Bảng 4.5 chỉ ra giá trị HTMT cho tất cả các cặp biến trong một ma trận, cho thấy tất cả HTMT đều nhỏ hơn nhiều so với ngưỡng quy định là 0,85.
Bảng 4.5: Giá trị HTMT
CI | EC | ED | EP | IE | PC | TBT | TC | |
CI | ||||||||
EC | 0,495 | |||||||
ED | 0,197 | 0,148 | ||||||
EP | 0,628 | 0,546 | 0,066 | |||||
IE | 0,558 | 0,486 | 0,136 | 0,631 | ||||
PC | 0,436 | 0,538 | 0,164 | 0,526 | 0,478 | |||
TBT | 0,463 | 0,519 | 0,375 | 0,246 | 0,478 | 0,357 | ||
TC | 0,517 | 0,447 | 0,177 | 0,586 | 0,533 | 0,341 | 0,438 |
(Nguồn: Kết quả xử lý dữ liệu của tác giả)
Ngoài ra, khi sử dụng chỉ tiêu HTMT, nên kiểm định xem các giá trị HTMT có khác 1 có ý nghĩa thống kê hay không. Do đó, đánh giá khoảng tin cậy bằng phương pháp complete boostrapping được thực hiện. Kết quả Bảng 7 (Phụ lục 3) trình bày cột 2,5% và 97,5% chỉ ra ngưỡng giới hạn thấp và cao của 95% khoảng tin cậy. Có thể thấy, khoảng tin cậy không bao gồm số 1. Như kỳ vọng, ngưỡng giới hạn thấp và cao của HTMT cho mối quan hệ giữa các cặp thang đo chứng minh giá trị phân biệt của tất cả các biến nghiên cứu. Tóm lại, Bảng 8 (Phụ lục 3) tổng kết các kết quả của mô hình đo lường, khẳng định rằng tất cả các tiêu chí đánh giá mô hình đều đạt, minh chứng cho độ tin cậy và giá trị.
4.3 Đánh giá mô hình cấu trúc PLS-SEM
Các tiêu chí được xem xét đánh giá mô hình cấu trúc tham chiếu theo nghiên cứu của Hair và cộng sự (2018). Luận án kiểm định với cỡ mẫu Bootstrapping N = 5000 (Henseler và cộng sự, 2015). Giá trị p-value < 1%, 5%, và 10%, các giả thuyết đề xuất được xem là có ý nghĩa thống kê ở độ tin cậy 99%, 95% và 90%. Từ kết quả ước lượng, luận án đưa ra các đánh giá như sau:
4.3.1 Đánh giá các vấn đề về cộng tuyến của mô hình cấu trúc
Theo quy trình, trước hết nghiên cứu cần kiểm tra mô hình cấu trúc về vấn đề cộng tuyến thông qua chỉ số VIF. Bảng 4.6 cho thấy tất cả giá trị VIF của các biến dự báo dưới ngưỡng 5. Vì vậy, cộng tuyến giữa các biến dự báo không phải là một vấn đề trong mô hình cấu trúc và có thể được tiếp tục kiểm tra báo cáo kết quả.
Bảng 4.6: Kết quả chỉ số VIF các biến dự báo của mô hình
Biến quan
sát | sát | sát | |||
CI1 | 1,545 | EMS1 | 1,916 | TC1 | 1,931 |
CI2 | 1,635 | EMS2 | 2,489 | TC2 | 2,400 |
CI3 | 1,602 | EMS3 | 2,391 | TC3 | 2,451 |
CI4 | 1,438 | EMS4 | 2,325 | TC4 | 3,286 |
CI5 | 1,640 | EP1 | 2,564 | TBT1 | 2,532 |
EC1 | 2,001 | EP2 | 2,708 | TBT2 | 2,837 |
Hệ số VIF
Biến quan
Hệ số VIF
Biến quan
Hệ số VIF
sát | sát | sát | |||
EC2 | 1,961 | EP3 | 2,332 | TBT3 | 3,280 |
EC3 | 1,780 | EP4 | 2,465 | TBT4 | 2,463 |
EC4 | 1,795 | EP5 | 2,412 | TBT5 | 2,444 |
EC5 | 1,832 | IE1 | 2,465 | PC1 | 3,067 |
ED1 | 3,220 | IE2 | 2,579 | PC2 | 2,980 |
ED2 | 3,014 | IE3 | 2,036 | PC3 | 2,696 |
ED3 | 3,143 | IE4 | 1,715 | PC4 | 1,754 |
ED4 | 2,947 |
Biến quan
Hệ số VIF
Biến quan
Hệ số VIF
Biến quan
Hệ số VIF
(Nguồn: Kết quả xử lý dữ liệu của tác giả)
Để đo lường sự phù hợp của mô hình, chỉ số SRMR và RMS theta được xem xét. Kết quả Bảng 4.7 cho thấy hệ số SRMR của mô hình tới hạn và mô hình ước lượng đều < 0,08. Chỉ số RMS theta < 0,12. Vì thế, mô hình ước lượng đạt yêu cầu về độ tương thích dữ liệu khảo sát so với dữ liệu thị trường.
Bảng 4.7: Đánh giá mức độ phù hợp mô hình
Mô hình tới hạn | Mô hình ước lượng | ||
SRMR | 0,044 | 0,044 | |
d_ULS | 1,617 | 1,617 | |
d_G | 0,678 | 0,678 | |
Chi-Square | 1331,990 | 1070,751 | |
NFI | 0,855 | 0,855 | |
RMS theta | 0,108 |
(Nguồn: Kết quả xử lý dữ liệu của tác giả)
4.3.2 Đánh giá hệ số xác định có điều chỉnh (R2)
Mức độ giải thích của các yếu tố ảnh hưởng (IE, EC, PC, TC, ED, CI, TBT) lên EMS và kết quả xuất khẩu lần lượt là 49,6 và 56,2. Trong đó, giá trị R2 hiệu chỉnh lần lượt là 48,5 và 55,2. Kết quả cho thấy mức độ giải thích của R2 hiệu chỉnh là vừa phải (nằm trong khoảng từ 0,25 đến 0,5) (Hair và cộng sự, 2018).
4.3.3 Đánh giá hệ số tác động (f2)
Độ lớn ảnh hưởng của các yếu tố tác động (IE, EC, PC, TC, ED, CI, TBT) lên EMS nằm trong khoảng từ 0,016 đến 0,042 (f2 CI->EMS = 0,042; f2 EC-> EMS = 0,027; f2 ED-> EMS = 0,016; f2 IE-> EMS = 0,037; f2 TC-> EMS = 0,027; f2 TBT->
EMS = 0,033; f2 PC-> EMS = 0,025). Trong đó, cường độ cạnh tranh (CI) ảnh hưởng lớn nhất đến EMS (f2= 0,042); sự khác biệt môi trường (ED) ảnh hưởng thấp nhất đến EMS (f2= 0,016) (Bảng 9, Phụ lục 3).
Độ lớn tác động của các yếu tố ảnh hưởng (IE, EC, PC, TC, ED, CI, TBT) đến kết quả xuất khẩu nằm trong khoảng từ 0,029 đến 0,082 (f2 CI->EP = 0,079; f2 EC-> kết quả xuất khẩu = 0,035; f2 ED-> kết quả xuất khẩu = 0,029; f2 EMS-> kết quả xuất khẩu = 0,030; f2 IE-> kết quả xuất khẩu = 0,073; f2 TC-> kết quả xuất khẩu = 0,082; f2 TBT-> kết quả xuất khẩu = 0,070; f2 PC-> kết quả xuất khẩu = 0,039). Trong đó, năng lực công nghệ (TC) ảnh hưởng lớn nhất đến kết quả xuất khẩu (f2= 0,082); sự khác biệt môi trường (ED) ảnh hưởng thấp nhất đến kết quả xuất khẩu (f2= 0,029). Tóm lại, giá trị tác động của các biến nội sinh (IE, EC, PC, TC, ED, CI, TBT) đến các biến dự báo (EMS, kết quả xuất khẩu) dao động từ mức ảnh hưởng yếu đến mức ảnh hưởng vừa (f2 = 0,02 -> f2 = 0,15) (Bảng 9, Phụ lục 3).
4.3.4 Đánh giá mức ý nghĩa và sự liên quan của các mối quan hệ trong mô hình cấu trúc
Sau khi chạy thủ tục, SmartPLS chỉ ra kết quả bootstraping cho mô hình cấu trúc. Giả định mức ý nghĩa 5%, Bảng 4.8 cho thấy rằng tất cả các mối quan hệ và các tác động tổng trong mô hình cấu trúc đều có ý nghĩa. Kết quả Bảng 4.9 minh hoạ trọng số gốc, giá trị trung bình bootstrap, chênh lệch giữa trọng số gốc và trọng số trung bình bootrstrap, khoảng tin cậy. Kết quả cho thấy sai lệch giữa giá trị bootstrap (N = 5000) và trọng số gốc là rất nhỏ. Hệ số đường dẫn đều nằm trong khoảng tin cậy từ 2,5% đến 97,5%. Do đó, ước lượng hệ số đường dẫn là đáng tin cậy.
Bảng 4.8: Kết quả ước lượng mô hình cấu trúc
Mối quan hệ
Trọng số gốc β
Trọng số B bootstraping
Độ lệch
T P
chuẩn
0,180 | 0,181 | 0,053 | 3,405 | 0,001 | |
CI -> EP | 0,234 | 0,232 | 0,044 | 5,315 | 0,000 |
EC -> EMS | 0,147 | 0,148 | 0,063 | 2,333 | 0,020 |
EC -> EP | 0,159 | 0,157 | 0,046 | 3,457 | 0,001 |
ED -> EMS | 0,095 | 0,093 | 0,045 | 2,125 | 0,034 |
ED -> EP | -0,121 | -0,122 | 0,041 | 2,918 | 0,004 |
EMS -> EP | 0,161 | 0,170 | 0,059 | 2,710 | 0,007 |
IE -> EMS | 0,174 | 0,174 | 0,050 | 3,465 | 0,001 |
IE -> EP | 0,232 | 0,228 | 0,056 | 4,138 | 0,000 |
TC -> EMS | 0,143 | 0,144 | 0,053 | 2,700 | 0,007 |
TC -> EP | 0,233 | 0,233 | 0,048 | 4,805 | 0,000 |
TBT-> EMS | 0,164 | 0,160 | 0,056 | 2,929 | 0,003 |
TBT -> EP | -0,225 | -0,228 | 0,050 | 4,510 | 0,000 |
PC -> EMS | 0,133 | 0,138 | 0,061 | 2,189 | 0,029 |
PC -> EP | 0,158 | 0,157 | 0,050 | 3,162 | 0,002 |
(Nguồn: Kết quả xử lý dữ liệu của tác giả)
4.3.5 Dự đoán mức độ dự báo phù hợp Q2 và q2
Nghiên cứu sử dụng kỹ thuật Blindfolding đánh giá sự liên quan mang tính dự báo của mô hình đường dẫn (Hair và cộng sự, 2018). Bảng kết quả về ước lượng phần dư giá trị chéo của khái niệm (Construct Cross Validated Redundance). Trong bảng SSO chỉ ra tổng của bình phương các quan sát, SSE tổng của bình phương sai số dự báo và cột cuối cùng là Q2(1 – SSE/SSO) thể hiện mức độ liên quan dự báo của mô hình với các biến nội sinh có liên quan.