Kết quả tính toán các hệ số chặn của 25 ngân hàng tác giả nêu trong bảng 4.15.
Bảng 4.15: Hệ số chặn của các ngân hàng
Hệ số chặn i | Mã ngân hàng | Hệ số chặn i | |
22 | 10.265 | 8 | 5.655 |
14 | 9.879 | 3 | 5.627 |
19 | 8.206 | 29 | 5.521 |
7 | 8.135 | 5 | 4.867 |
1 | 7.353 | 20 | 4.615 |
28 | 7.194 | 18 | 4.382 |
17 | 6.908 | 27 | 4.351 |
2 | 6.645 | 25 | 4.057 |
4 | 6.320 | 33 | 3.858 |
26 | 6.119 | 10 | 3.189 |
24 | 5.952 | 21 | 2.730 |
31 | 5.915 | 6 | -0.982 |
32 | 5.809 |
Có thể bạn quan tâm!
-
Tỷ Lệ Nợ Xấu Các Nhtm Việt Nam Giai Đoạn 2009 -2015 -
Thống Kê Mô Tả Của Các Biến Đầu Vào/đầu Ra Mô Hình Dea -
Các Biến Nghiên Cứu Và Hệ Số Tương Quan Với Biến Phụ Thuộc -
Tác Động Biên Của Các Biến Đến Xác Suất Vỡ Nợ P -
Bảng So Sánh Kết Quả Xếp Loại -
Xây dựng mô hình cảnh báo nguy cơ vỡ nợ đối với các ngân hàng thương mại cổ phần Việt Nam - 18
Xem toàn bộ 168 trang tài liệu này.
Nguồn: Tính toán của tác giả
Kết quả mô hình :
ln(
p 1 p
) i
-1.2955*R G D P 1.0346 * d 3 2.014 * e11 3.0769 * l3
trong đó p là xác suất để quan sát thuộc nhóm nguy cơ vỡ nợ cao.
Ký hiệu tỷ số O d d s
không vỡ nợ bao nhiêu lần.
p 1 p
, tỷ số này cho biết xác suất vỡ nợ lớn hơn xác suất
Các biến số trong mô hình:
RGDP: Tốc độ tăng trưởng tổng sản phẩm quốc dân
d3: Nợ quá hạn/tổng nợ phải trả
e11: Lãi cận biên
l3: Các khoản cho vay thuần/tiền gửi của khách
+ Với mức ý nghĩa 6% biến RGDP tác động ngược chiều đến xác suất p, trong khi đó với mức ý nghĩa 1% biến e11 tác động ngược chiều đến p.
+ Với mức ý nghĩa 1% biến d3 tác động cùng chiều đến p và với mức ý nghĩa 6% biến l3 tác động cùng chiều đến p.
Tính xác suất vỡ nợ và đo hiệu suất của mô hình, kết quả phân nhóm đúng của mô hình Logit dữ liệu mảng tác giả trình bày trong bảng 4.16.
Bảng 4.16: Hiệu suất phân loại của mô hình LA
Dự báo | ||||
Y | % đúng | |||
0 | 1 | |||
Y | 0 | 69 | 6 | 92% |
1 | 8 | 31 | 79.48% | |
87.71% | ||||
Nguồn: Tính toán của tác giả
Với bộ dữ liệu 114 quan sát sử dụng ước lượng mô hình Logit: Có 75 quan sát thuộc nhóm Y = 0, mô hình phân nhóm đúng 69 quan sát đạt tỷ lệ 92%, trong 39 quan sát có Y = 1, mô hình phân nhóm đúng 31 quan sát chiếm tỷ lệ 79.48 %, tổng kết lại mô hình phân nhóm đúng 100 quan sát trong tổng số 114 quan sát của dữ liệu 5 năm 2010-2014 như vậy hiệu suất đạt 87.71%.
Căn cứ vào độ lớn của các hệ số ước lượng tác giả nhận thấy
+ Nếu biến RGDP tăng 1% trong khi các biến khác không đổi thì tỷ số giữa xác suất vỡ nợ và xác suất không vỡ nợ (Odds) giảm 3.65 lần.
+ Nếu biến d3 tăng 1% trong khi các biến khác không đổi thì Odds tăng 2.814 lần
+ Nếu biến e11 tăng 1% trong khi các biến khác không đổi thì Odds giảm 7.5 lần
+ Nếu biến l3 tăng 1% trong khi các biến khác không đổi thì Odds tăng 1.03 lần Sau đây, tác giả phân tích một số quan sát với các giá trị các biến cụ thể
Bảng 4.17: Phân tích một số quan sát
Năm | RGDP | e11 | d3 | l3 | Xác suất | Odds | RGDP giảm 1% | e11 giảm 1% | d3 tăng 1% | l3 tăng 1% | |
32 | 2010 | 0.0678 | 0.0270 | 0.0209 | 1.3935 | 0.1234 | 0.1408 | 0.5139 | 1.0559 | 0.3962 | 0.1450 |
2 | 2014 | 0.0598 | 0.0293 | 0.0331 | 0.7421 | 0.2137 | 0.2717 | 0.9918 | 2.0379 | 0.7646 | 0.2799 |
36 | 2010 | 0.0678 | 0.0264 | 0.0092 | 0.6891 | 0.3164 | 0.4627 | 1.6890 | 3.4706 | 1.3022 | 0.4766 |
32 | 2011 | 0.0589 | 0.0298 | 0.0216 | 1.5716 | 0.3188 | 0.4679 | 1.7079 | 3.5094 | 1.3167 | 0.4820 |
5 | 2014 | 0.0598 | 0.0164 | 0.0314 | 0.7825 | 0.3714 | 0.5909 | 2.1568 | 4.4319 | 1.6628 | 0.6086 |
32 | 2014 | 0.0598 | 0.0133 | 0.0171 | 0.7904 | 0.3977 | 0.6604 | 2.4105 | 4.9530 | 1.8584 | 0.6802 |
Nguồn: Tính toán của tác giả
Ngân hàng mã 32 năm 2010, chỉ tiêu Odds có giá trị 0.14 biến phụ thuộc đang nhận giá trị Y = 0.
+ Nếu biến RGDP giảm 1% thì quan sát có tỷ lệ Odds tăng lên mức 0.51, quan sát có Y= 0, nguy cơ vỡ nợ thấp.
+ Nếu biến d3 tăng 1% thì Odds đạt giá trị 0.39 và quan sát vẫn có Y = 0.
+ Nếu biến e11 giảm 1% thì tỷ lệ Odds là 1.059 do đó quan sát có Y = 1, tức quan sát chuyển sang mức nguy cơ vỡ nợ cao.
Bảng 4.17 tác giả phân tích thêm 5 quan sát khi cho lần lượt các biến RGDP, e11, d3, l3 thay đổi 1% (trong khi các biến khác giữ nguyên). Theo kết quả tính toán
của tác giả nếu các quan sát đang có mức xác suất p 26.2% mà biến d3 tăng 1% thì
quan sát sẽ chuyển sang mức nguy cơ cao. Do vậy với các ngân hàng có xác suất
p 26.2% cần đặc biệt chú ý biến d3, cũng có thể xem mức xác suất p = 26.2% là
mức xác suất cảnh báo sớm. Đối với các quan sát p 11.76% chú ý đến biến e11.
Bảng 4.15 tổng hợp các hệ số chặn riêng thể hiện tính đặc thù của các ngân hàng ảnh hưởng đến khả năng vỡ nợ, tính đặc thù này có thể gây bởi lĩnh vực hoạt động, cấu trúc vốn, công nghệ, nhân sự,…của từng ngân hàng. Kết quả chỉ ra các ngân hàng có mã nghiên cứu là 22,14, 19, 7 có hệ số chặn lớn tiềm ẩn nguy cơ vỡ nợ cao hơn so với các NH khác.
Với ngân hàng có mã 22, trong giai đoạn 2010-2011 ngân hàng đã gặp khó khăn lớn về thanh khoản. Sau đó, NHNN thanh tra và đưa vào danh sách 9 ngân hàng
yếu kém cần giám sát. Theo báo cáo gửi đại hội cổ đông của ngân hàng này ngày 3/4/2013 thì giá trị nợ quá hạn của ngân hàng năm 2011 là 3333 tỷ đồng, chiếm 37.6% tổng dư nợ. Ngày 16/9/2013, NHNN quyết định cho hợp nhất Ngân hàng này với một công ty tài chính khác.
Với ngân hàng có mã 19, đây là ngân hàng trong giai đoạn 2010-2013 đã huy động mạnh tiền gửi với mức lãi suất vượt trần quy định, ngân hàng đã cho vay không đúng quy định, nhiều khoản vay đã không có khả năng thu hồi. Năm 2014, NHNN tiến hành thanh tra và đánh giá nợ xấu của ngân hàng này lớn gấp 2 lần vốn chủ sở hữu. Ngày 6/5/2015, NHNN đã ra quyết định mua bắt buộc Ngân hàng này với giá 0 đồng.
Với ngân hàng có mã 14 và mã 7, trong giai đoạn 2010-2013, hai ngân hàng này có tỷ lệ huy động từ thị trường liên ngân hàng/ tổng huy động rất cao phản ánh rủi ro thanh khoản lớn, các ngân hàng bị mất cân đối dòng tiền vào ra, cần xem xét toàn diện để xác định nguyên nhân, đề ra giải pháp hạn chế nguy cơ vỡ nợ.
4.3. Mô hình mạng nơron
Vào cuối những năm 1980, mạng nơ ron bắt đầu xuất hiện và đến năm 1990 trở thành một công cụ cơ bản được sử dụng trong các nghiên cứu vỡ nợ, vỡ nợ ngân hàng. Nhiều nghiên cứu đã chỉ ra rằng, mạng nơ ron thành công hơn một số mô hình thống kê (mô hình Logit, mô hình MDA) trong nghiên cứu cảnh báo vỡ nợ. Sau khi thực nghiệm mô hình Logit trong nghiên cứu và chỉ ra các nhân tố tác động đến nguy cơ vỡ nợ của các NHTMCP, để có cơ sở phân tích, so sánh, lựa chọn, đề xuất mô hình, tác giả thực nghiệm áp dụng mô hình mạng nơ ron, cây quyết định- hai mô hình thuộc nhóm mô hình sử dụng kỹ thuật thông minh. Mạng nơ ron được thực nghiệm để kiểm tra khả năng dự báo của nhóm biến độc lập, đánh giá hiệu suất dự báo.
Dữ liệu sử dụng trong mô hình mạng nơron gồm 163 quan sát. Các quan sát
được chia một cách ngẫu nhiên thành 3 mẫu con, đó là:
(i) Mẫu huấn luyện dùng cho quá trình huấn luyện (điều chỉnh các trọng số liên kết) gồm 115 quan sát.
(ii) Mẫu thứ hai gọi là mẫu dữ liệu chứng thực gồm 24 quan sát dùng để đo năng lực khái quát hóa của mạng và dừng thủ tục học khi năng lực mạng không được cải thiện.
(iii) Mẫu thứ ba dùng để kiểm tra gồm 24 quan sát. Phần mẫu này không tác động đến chương trình học và nó cung cấp độ đo độc lập đo hiệu suất của mạng trong suốt quá trình cũng như sau khi học.
107
Tiếp theo để xác định số nơ ron tối ưu trong nút ẩn tác giả sử dụng quá trình lặp xem xét số lượng nơron cho đến khi tìm được lỗi trung bình bình phương (MSE) nhỏ nhất. Theo kết quả đó, tác giả sử dụng mạng nơ ron với 10 nút ẩn (Hình 4.3).
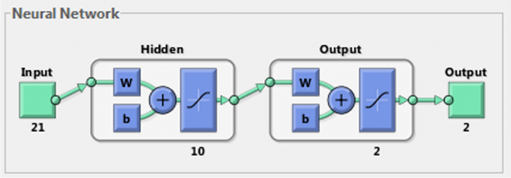
Hình 4.3: Mạng nơ ron với 10 nút ẩn
Nguồn: Thiết kế của tác giả
Cấu trúc mạng nơron của tác giả bao gồm 21 nút đầu vào ứng với 18 biến ở bảng 4.9 và 3 biến vĩ mô ở bảng 4.8, 10 nút tầng ẩn và 2 nút đầu ra. Quá trình huấn luyện mạng tiến hành qua nhiều lần và dừng khi ta đạt được hiệu suất như kỳ vọng. Các thông số của mạng nơron biểu diễn ở bảng 4.18.
Bảng 4.18: Các thông số của mạng nơ ron
Số lượng quan sát | MSE | |
Mẫu huấn luyện | 115 | 0.049 |
Mẫu chứng thực | 24 | 0.047 |
Mẫu kiểm tra | 24 | 0.046 |
Nguồn: Tính toán của tác giả
Hiệu suất phân nhóm của mạng nơron trên các mẫu huấn luyện, mẫu chứng thực, mẫu kiểm tra được mô tả ở bảng 4.19.
Bảng 4.19: Hiệu suất của mạng nơron
Mẫu huấn luyện | Mẫu chứng thực | Mẫu kiểm tra | |
Hiệu suất | 95% | 91.6% | 91.6% |
Nguồn: Tính toán của tác giả
Để có cơ sở so sánh hiệu suất hai mô hình Logit và mô hình mạng nơron tác giả tính toán hiệu suất của mô hình ANN trên bộ dữ liệu 114 quan sát (bộ dữ liệu đã sử dụng để ước lượng mô hình Logit với dữ liệu mảng) thì tỷ lệ phân nhóm đúng của mô hình ANN như sau
Bảng 4.20: Hiệu suất phân loại của mô hình ANN
Dự báo | ||||
Y | % đúng | |||
0 | 1 | |||
Y | 0 | 74 | 1 | 98.66% |
1 | 7 | 32 | 82.05% | |
92.98% | ||||
Nguồn: Tính toán của tác giả
Trong 75 quan sát thuộc nhóm Y = 0, mô hình ANN phân nhóm đúng 74 quan sát đạt tỷ lệ 98.66%, trong 39 quan sát có Y = 1, mô hình phân nhóm đúng 32 quan sát chiếm tỷ lệ 82.05%, tổng kết lại mô hình phân nhóm đúng 106 quan sát trong tổng số 114 quan sát như vậy hiệu suất đạt 92.98%.
So sánh hai mô hình Logit dữ liệu mảng và mô hình ANN tác giả nhận thấy mạng nơron có hiệu suất phân nhóm (92.98%) cao hơn hiệu suất của mô hình Logit (87.71%). Tuy nhiên qua việc thực nghiệm mạng nơ ron tác giả nhận thấy hạn chế của mạng nơ ron là mô hình không chỉ ra các nhân tố, các chỉ tiêu tác động tới nguy cơ vỡ nợ.
4.4. Mô hình cây quyết định
Gần đây việc sử dụng các mô hình phi tham số, tận dụng thế mạnh của máy tính trong nghiên cứu kinh tế học được phát triển mạnh mẽ, trong số các mô hình đó phải kể đến mô hình cây quyết định. Cây quyết định đã được sử dụng phổ biến cho các vấn đề phân loại, bởi vì quy tắc phân loại của nó là dễ hiểu, dễ áp dụng. Sau đây, luận án thực nghiệm mô hình cây quyết định để dự báo nguy cơ vỡ nợ cho các NHTMCP Việt Nam, tác giả kiểm tra khả năng dự báo của các biến độc lập, xác định các biến số giúp phân loại các ngân hàng.
Tác giả sử dụng các quan sát trong các năm từ năm 2010 đến năm 2014, gồm 163 quan sát. Để phù hợp với thiết kế mô hình cây quyết định, tác giả chuyển biến phụ thuộc trong file dữ liệu sang dạng dữ liệu định danh. Quan sát thuộc nhóm nguy cơ vỡ nợ cao được ký hiệu là Y, quan sát thuộc nhóm nguy cơ thấp ký hiệu là N. Biến độc lập sử dụng xây dựng cây quyết định gồm 18 biến trong bảng 4.9 và 3 biến vĩ mô trong bảng 4.8. Tác giả sử dụng thuật toán J48 trên phần mềm Weka phiên bản 3.6.9 để tạo cây quyết định.
Bảng 4.21: Thuật toán J48
Input: training dataset T; attributes S.
Output: decision Tree 1: if T is NULL then 2: return failure
3: end if
4: if S is NULL then
5: return Tree as a single node with most frequent class label in T 6: end if
7: if S 1 then
8: return Tree as a single node S 9: end if
10: set Tree ={} 11: for a S do
12: set Info(a, T)= 0 and Split Info(a,T) = 0 13: compute Entropy (a)
14: for v values(a,T ) do
15: set Ta,v
as the subset of T with attribute a = v
Ta , v
Tv
16: Info ( a , T )
E ntropy ( a , v )
17:
SplitInfor ( a , T )
log
Ta ,v
Tv
Ta ,v
Tv
18: end for
19: Gain(a,T ) Entropy(a) Infor (a,T )
20: GainRatio(a,T ) Gain(a,T )
Split Info(a,T )
21: end for
22:
set abest arg max GainRatio(a,T )
b es t
23: attach a into Tree
b es t do
24: for v v a lu e s ( a , T )
end for return Tree
Nguồn: Wei Dai và Wei Ji (2014)
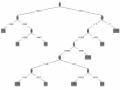
Kết quả mô hình được nêu chi tiết ở bảng 4.22.
Bảng 4.22: Kết quả của cây quyết định
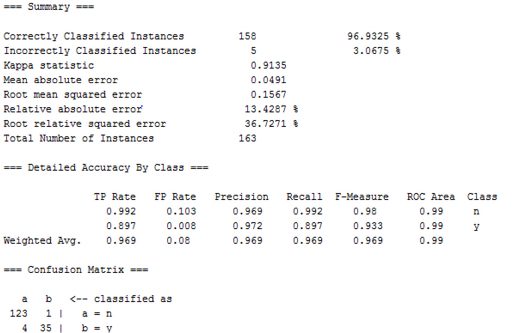
Nguồn: Tính toán của tác giả
Cụ thể, trong 39 quan sát có nhãn Y thì cây quyết định dán dãn đúng là 35 đạt hiệu suất 89.74%, trong số 124 quan sát có nhãn N, cây quyết định dán nhãn đúng là 123 đạt hiệu suất 99.19%, kết quả tổng hợp cây quyết định dán dãn đúng 158 quan sát đạt hiệu suất 96.93%, chỉ có 5 quan sát bị dán dãn sai. Hiệu suất phân nhóm của cây quyết định là khá cao.
Thuật toán trong cây quyết định chỉ ra 5 chỉ tiêu tốt giúp cho việc phân loại.
Nội dung các chỉ tiêu này nêu trong bảng 4.23.
Bảng 4.23: Các biến xây dựng cây quyết định
Nội dung | |
e2 | ROE |
d3 | Nợ quá hạn/Tổng nợ phải trả |
m2 | (Lợi nhuận trước thuế và dự phòng)/Chi phí hoạt động |
a2 | Dự phòng nợ khó đòi/ dư nợ cho vay |
a3 | Nợ khó đòi/(vốn chủ sở hữu và dự phòng nợ khó đòi) |
Nguồn: Tính toán của tác giả