Định Luật Cơ Bản Của Hiện Tượng Cảm Ứng Điện Từ

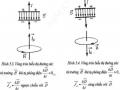
 Khi đưa nam châm tiến lại gần và khi đưa nam châm ra xa ống dây thì kim điện kế bị lệch về hai phía khác nhau vậy chiều dòng điện khác nhau.

 Nếu dịch chuyển nam châm lại gần hoặc ra xa ống dây với tốc độ khác nhau thì cường dòng điện xuất hiện cũng khác nhau. Cường độ dòng điện mạnh khi tốc độ dịch chuyển tương đối lớn và ngược lại.

 Nếu thay nam châm vĩnh cửu bằng một nam châm điện và thay đổi độ lớn cường độ dòng điện chạy qua chúng ta cũng thu được những kết quả tương tự.

Giải thích:

Qua các kết quả thí nghiệm đã làm Faraday phát hiện ra rằng khi nam châm dịch chuyển hoặc thay đổi cường độ dòng điện chạy qua nam châm điện đều làm cho từ thông gửi qua ống dây biến thiên. Dựa vào những phân tích của mình ông đưa ra một số kết luận:

 Nguyên nhân xuất hiện dòng điện chạy trong mạch là do có sự biến thiên từ thông gửi qua diện tích mạch điện. Dòng điện xuất hiện trên mạch khi có sự biến thiên từ thông gọi là dòng điện cảm ứng, hiện tượng xuất hiện dòng điện cảm ứng khi có sự biến thiên từ thông gọi là hiện tượng cảm ứng điện từ.

 Dòng điện cảm ứng chỉ tồn tại trong khoảng thời gian có sự biến thiên từ thông.

 Chiều của dòng điện cảm ứng phụ thuộc vào sự tăng hay giảm của từ thông.

 Cường độ dòng điện cảm ứng tỉ lệ thuận với tốc độ biến thiên từ thông gửi qua mạch.

Có thể bạn quan tâm!

Xem toàn bộ 258 trang tài liệu này.

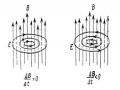
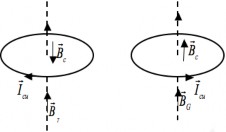
4.1.2. Định luật Lenx

Qua việc nghiên cứu thí nghiệm của

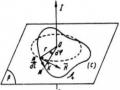
Hình 4.2

Faraday, Lenx nhận thấy có mối liên hệ chặt chẽ giữa chiều của dòng điện cảm ứng và sự tăng giảm của từ thông ông đã đi tìm hiểu mối liên hệ giữa

chúng và rút ra được định luật nêu lên cách xác định chiều của dòng điện cảm ứng chạy trên một đoạn mạch.

Dòng điện cảm ứng phải có chiều sao cho từ trường do nó sinh ra có tác dụng chống lại nguyên nhân sinh ra nó.

Vận dụng định luật Lenx, ta có thể xác định chiều của dòng điện cảm ứng xuất hiện trên đoạn mạch trong hai trường như Hình 4.2.

4.1.3. Định luật cơ bản của hiện tượng cảm ứng điện từ

Sự xuất hiện dòng điện cảm ứng chứng tỏ trong đoạn mạch suất hiện một sức điện động. Sức điện động đó gọi là sức điện động cảm ứng.

Để xác định sức điện động cảm ứng, ta xét một khung dây kín (C) trong từ trường như Hình 4.3. Trong thời gian dt khung dây dịch chuyển, từ thông gửi qua khung dây biến thiên một lượng dkhi đó dòng điện xuất hiện trong mạch là Ic. Công của lực

từ tác dụng lên dòng điện cảm ứng bằng dA Icd.

Hình 4.3

Mặt khác theo định luật Lenx, lực từ đóng vai trò cản trở sự dịch chuyển của vòng dây vậy công dA đóng vai trò là công cản. Gọi dA' là công cơ học làm dịch chuyển khung dây và công này chuyển hóa thàng năng lượng của dòng điện cảm ứng. Vậy ta có:

dA' dA Icd(4.1)

Lấy C là suất điện động cảm ứng thì năng lượng của dòng điện cảm ứng trong khoảng thời gian dt bằng C IC dt do đó ta có:

dA' C IC dt (4.2)

Từ (4.1) và (4.2), ta viết được:

IC dC IC dt

d

C dt

(4.3)

Vậy:

Sức điện động về trị số bằng nhưng trái dấu với tốc độ biến thiên của từ thông gửi qua diện tích mạch điện.

Dấu (-) trong biểu thức (4.3) biểu diễn về mặt toán học của định luật Lenx.

4.1.4. Nguyên tắc tạo ra dòng điện xoay chiều

Để tạo ra dòng điện xoay chiều như chúng ta đang sử dụng người ta quay đều một khung dây trong từ trường không đổi, khi đó từ thông gửi qua khung sẽ biến thiên và trong khung xuất hiện một dòng điện xoay chiều.

Giả sử khung dây có N vòng dây quay đều quanh trục với tốc độ góc

. Gọi S là diện tích của khung, thời điểm ban đầu vectơ pháp tuyến n của khung hợp với cảm ứng từ B góc 0 . Tại thời điểm t góc hợp bởi giữa n và B là t 0 .

Từ thông gửi qua diện tích giới hạn của khung dây tại thời điểm t là:

NBS cos(t 0 ) (4.4) Thay (4.4) vào (4.3) ta có:

dNBS sin(t )

C dt0

(4.5)

Vì suất điện động cảm ứng biến thiên điều hòa theo thời gian nên dòng diện cảm ứng cũng biến thiên điều hòa theo thời gian và được biểu diễn dưới dạng:

i I0 sin(t 0i ) (4.6)

Vậy, khi có khung dây quay đều trong từ trường đều ta có thể tạo nên một dòng điện xoay chiều. Đó cũng là nguyên tắc tạo ra dòng điện xoay chiều.

Bài toán 1:

Một thanh dây dẫn dài

l  20cm

chuyển động với tốc độ 15m / s

trong một

từ trường đều cảm ứng từ B  0,3T . Tìm độ lớn suất điện động cảm ứng xuất

hiện trên thanh, biết rằng trong quá trình chuyển động thanh luôn vuông góc với đường sức từ và phương dịch chuyển.

Giải:

Theo định luật cơ bản của hiện tượng cảm ứng điện từ ta có:

| |d

dt

Ta có:

Vậy:

dBdS B.dS.cosB.l.dx

| |dB.l.dx Blv  0, 3.0, 2.15  0, 9 (V )

dt dt

4.1.5. Dòng điện Foucoult

Khi đặt một vật dẫn có kích thước lớn vào một từ trường biến thiên theo thời gian. Do có sự biến thiên từ thông nên trong thể tích các vật đó xuất hiện các dòng điện xoáy gọi là dòng điện Foucoul. Do vật dẫn có kích thước lớn nên điện trở của nó nhỏ, cường độ dòng điện Foucoul là:

I C

F R

(4.7)

Vì điện trở của vật dẫn nhỏ và suất điện động cảm ứng lớn nên dòng điện Foucoul có tác dụng đáng kể trong các dụng cụ điện nhất là trong các dòng điện cao tần. Trong các máy biến thế, động cơ điện... dòng điện Foucoul có tác hại do là nóng các dụng cụ điện đó. Nhưng chúng ta cũng lợi dụng dòng điện Foucoul để nấu chảy kim loại.

4.2. HIỆN TƯỢNG TỰ CẢM

4.2.1. Hiện tượng

Khi có dòng điện biến thiên chạy qua một đoạn mạch kín (C) thì từ trường của dòng điện

116

Hình 4.4

sinh ra sẽ biến thiên. Từ trường biến thiên này tạo nên sự biến thiên từ thông gửi qua diện tích giới hạn mạch (C) khi đó trên đoạn mạch xuất hiện dòng

điện cảm ứng

I C . Dòng I C

xuất hiện không phải do các yếu tố bên ngoài mà

do chính dòng điện chạy trong mạch, nên I C

hiện tượng trên gọi là hiện tượng tự cảm.

được gọi là dòng điện tự cảm và

Trong các mạch điện một chiều dòng tự cảm thường xuất hiện khi đóng hoặc mở mạch, đối với mạch điện xoay chiều thì dòng tự cảm luôn xuất hiện do dòng điện luôn biến thiên.

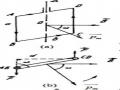
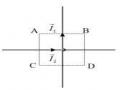
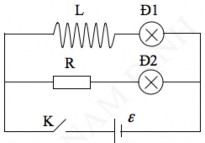
Để kiểm chứng sự xuất hiện của dòng tự cảm ta xét thí nghiệm được

mô tả trên Hình 4.4. Hai đèn

Đ1 và Đ2

giống nhau, điện trở của cuộn dây trên

đoạn AB bằng điện trở R của nhánh CD. Khi khóa K đóng ta quan sát thấy đèn

Đ1 sáng lên từ từ còn đèn Đ2

sáng lên ngay, sau một khoảng thời gian ngắn

hai đèn sáng như nhau. Khi K mở đèn Đ2

trước khi tắt.

tắt ngay còn đèn

Đ1 bừng sáng

Hiện tượng trên được giải thích là do có sự xuất hiện dòng điện cảm ứng trong khoảng thời gian lúc khóa K đóng hoặc mở. Khi đóng K từ thông trong cuộn dây của nhánh AB tăng từ 0 đến làm xuất hiện trên ống dây một dòng điện cảm ứng. Theo định luật Lenx dòng điện này ngược chiều với dòng

điện do nguồn cung cấp do đó Đ1 sáng lên từ từ .

Khi K mở từ thông trong cuộn dây của nhánh AB giảm từ đến 0, xuất hiện trên ống dây một dòng điện cảm ứng. Theo định luật Lenx dòng

điện này cùng chiều với dòng điện do nguồn cung cấp do đó Đ1 bừng sáng

trước khi tắt. Hiện tượng trên không xảy ra với nhánh CD do không có cuộn dây.

4.2.2. Sức điện động tự cảm

Sức điện động gây nên dòng tự cảm gọi là sức điện động tự cảm. Do hiện tượng tự cảm có bản chất là hiện tượng cảm ứng điện từ nên sức điện động tự cảm được xác định bởi:

tc

d

dt

(4.8)

trong đó từ thông do dòng điện chạy trong mạch sinh ra và gửi qua diện tích mạch điện đó.

Mặt khác, tỉ lệ thuận với cảm ứng từ do dòng điện đó sinh ra, mà cảm ứng từ lại tỉ lệ thuận với cường độ dòng điện, do đó ta có:

Li (4.9)

với L là hệ số tỉ lệ phụ thuộc vào hình dạng kích thước của đoạn mạch, L gọi là

hệ số tự cảm của đoạn mạch.

Thay (4.9) vào (4.8) ta được:

d(Li) L di

(4.10)

tc dt dt

Như vậy:

Sức điện động tự cảm tỉ lệ thuận với tốc độ biến thiên cường độ dòng điện chạy trong đoạn mạch.

Đơn vị của hệ số tự cảm là Henry: 1H 1Wb

1A

Henry là hệ số tự cảm của một đoạn mạch mà khi có dòng điện bằng một Amper chạy qua thì nó sinh ra trong chân không từ thông bằng một vêbe gửi qua diện tích mạch đó.

4.3. NĂNG LƯỢNG CỦA TỪ TRƯỜNG

4.3.1. Năng lượng từ trường của ống dây điện

0

Xét một đoạn mạch gồm có một cuộn dây có hệ số tự cảm L, nguồn điện sức điện động điện trở R và khóa K như hình vẽ. Khi khóa K đóng dòng điện do nguồn cung cấp là i0 , toàn bộ năng lượng do nguồn cung cấp đều biến đổi thành nhiệt theo định luật Jun – Lenx ( Q i2 ). Điều này chỉ

đúng khi dòng điện trong mạch đạt trạng thái ổn định.

Trong khoảng thời gian mở khóa K xuất hiện dòng điện tự cảm, do đó dòng điện trong mạch khi mở và khi đóng khóa là:

id i0 itc ; im i0 itc (4.11)

Do đó khi đóng K điện năng do dòng điện phát ra sẽ lớn hơn điện năng trong mạch và khi mở K thì ngược lại. Như vậy, khi đóng mạch một phần năng lượng điện sinh ra đã được tiềm tàng dưới một dạng năng lượng nào đó, khi mở mạch thì phần năng lượng này chuyển hóa thành nhiệt trong mạch.

Mặt khác, khi đóng mạch thì trong mạch có từ trường và khi mở mạch từ trường này mất đi, mà từ trường là một dạng vật chất mang năng lượng vậy phần năng lượng tiềm tàng nói trên chính là năng lượng của từ trường.

Thí nghiệm trên đã chứng tỏ về mặt định tính từ trường mang năng lượng. Ta sẽ tính năng lượng này.

Áp dụng định luật Ohm cho mạch điện khi đóng khóa K ta có

tc Ri (4.12)

trong đó R là điện trở của toàn mạch. Theo (4.10) ta có:

tc

L di

dt

Thay vào (4.12) ta được:

Ri L di

dt

Nhân cả hai vế (4.13) với idt :

(4.13)

idt Ri2dt Lidi (4.14)

Từ (4.14) ta thấy idt chính là phần năng lượng do nguồn điện sinh ra trong khoảng thời gian dt, năng lượng này gồm hai phần: một phần tỏa nhiệt trên điện trở ( Ri2 dt ); phần còn lại chuyển hóa thành năng lượng của từ trường sinh ra. Gọi dW là phần năng lượng đó, ta có:

dW Lidi (4.15)

Năng lượng của dòng điện được chuyển hóa thành năng lượng từ trường trong ống dây điện là:

I

W Li di

0

(4.16)

Lấy tích phân, ta được:

2

W LI

2

(4.17)

Công thức (4.17) xác định năng lượng từ trường trong ống dây.

4.3.2. Năng lượng của từ trường

Như chúng ta đã biết từ trường mang năng lượng, nói chung từ trường tại các điểm khác nhau có độ lớn khác nhau vậy năng lượng của từ trường phân bố không đều. Năng lượng từ trường tại mỗi điểm được xác định bằng mật độ năng lượng từ trường.

Để xác định biểu thức mật độ năng lượng bất kì trước hết ta xác định mật độ từ trường trong ống dây. Gọi V là thể tích của ống dây, mật độ từ trường được xác định bởi:

w W

V

2

W LI 1 (

N 2 S

(4.18)

2 (4.19)

2 2 0 l )I

Với V lS, l là chiều dài của ống dây; S là diện tích của mỗi vòng dây; N

là số vòng dây trên ống dây.

Mặt khác, từ trường trong ống dây được xác định bởi:

B 0nI 0

N I (4.20)

l

Thay (4.20) vào (4.19) ta được:

2

w  1 B

(4.21)

2 0

Xem tất cả 258 trang.

Ngày đăng: 16/07/2022

Trang chủ Tài liệu miễn phí