Tác Dụng Của Từ Trường Lên Một Phần Tử Dòng Điện

3.4. ĐỊNH LÝ AMPER VỀ DÒNG TOÀN PHẦN

3.4.1. Lưu số của vectơ cường độ từ trường

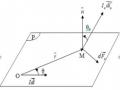
Xét một đường cong kín (C) nằm trong một từ trường bất kì. Chia (C) thành các đoạn nhỏ dl có độ dài dl , có phương trùng với phương của đoạn dl và có chiều trùng với chiều dịch chuyển trên đường cong (C). Người ta gọi

dl là vectơ dịch chuyển. Giả sử cường độ từ trường trên dl là H .

Định nghĩa lưu số của vectơ cường độ từ trường:

Lưu số vectơ của cường độ từ trường dọc theo một đường cong kín (C) là đại lượng được tính bằng tích phân vectơ H dọc theo toàn bộ đường cong kín đó:

Có thể bạn quan tâm!

Xem toàn bộ 258 trang tài liệu này.

Hdl

Hdl cos

(3.23)

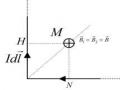
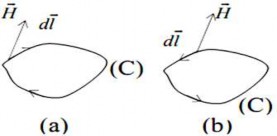
Hình 3.8. a. Lưu số có giá trị dương

trong đó α là góc hợp bởi vectơ H và d l .

Nhận xét:

b. Lưu số có giá trị âm

Nếu  900 nghĩa là chiều dịch chuyển của đường cong (C) thuận với chiều của các đường cảm ứng từ thì lưu số có giá trị dương Hình 3.8a.

Nếu  900 nghĩa là chiều dịch chuyển của đường cong (C) ngược với chiều của các đường cảm ứng từ thì lưu số có giá trị âm Hình 3.8b .

3.4.2. Định lý Amper về dòng điện toàn phần

Định lý Amper về dòng điện toàn phần nêu lên mối liên hệ giữa lưu số của vectơ cường độ từ trường dọc theo một đường cong kín (C) và các dòng điện xuyên qua diện tích giới hạn của (C).

Giả sử ta xét từ trường gây ra bởi một dòng điện thẳng dài vô hạn có cường độ I.

Ta lấy một đường sức nằm trong mặt phẳng (P) vuông góc với dòng điện và một đường cong (C) có dạng bất kì cũng nằm trong mặt phẳng (P).

Vectơ cường độ từ trường tại điểm M bất kì trên đường cong (C) cách dòng điện một khoảng r có độ lớn:

H I

2r

Lưu số của vectơ cường độ từ trường dọc theo (C) là:

I

dl.cos

Hdl Hdl cos2r

C C C

Mặt khác dl .cosrd thay vào biểu thức lưu số ta được:



I

Hdl

d

2C

(3.24)

a. Trường hợp (C) bao quanh dòng điện

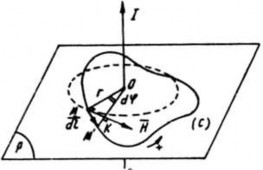
Nếu (C) bao quanh dòng điện, ta có:



I

Hdl

dI

2C

(3.25)

Trong đó, I sẽ có dấu dương nếu nó có chiều sao cho đường cảm ứng từ do nó gây ra cùng chiều với chiều dịch chuyển của đường cong (C), nếu ngược lại thì I sẽ có dấu âm.

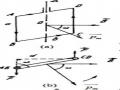
b. Trường hợp (C) không bao quanh dòng điện

Hình 3.9

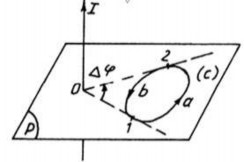
Nếu (C) không bao quanh dòng điện thì ta chia đường cong thành hai phần 1a2 và 2b1 bằng hai tiếp tuyến O1 và O2 vạch từ dòng điện đến đường cong Hình 3.10. Gọi là góc giữa O1 và O2.

Lưu số của vectơ cường độ từ trường trên đường cong (C) là:



  I I I 1

H dl

d

2C 2

d

2

1a 2

d ()

2

2b1

H dl  0

Trong trường hợp từ trường gây bởi dòng điện có hình dạng bất kì và

c. Trường hợp từ trường gây ra bởi nhiều dòng điện

Nếu từ trường gây ra bởi nhiều dòng điện, có cường độ lần lượt là I1, I2,…,In thì theo nguyên lý chồng chất từ trường ta có:

H H1 H2  ... Hn

Khi đó lưu số của vectơ cường độ từ trường là:

Hình 3.10

      n

H dl H1H2...Hndl Ik

(3.26)

C C k1

Biểu thức này chính là định lý Amper về dòng điện toàn phần.

Định lý Amper về dòng toàn phần:

Lưu số của vectơ cường độ từ trường dọc theo một vòng của đường cong kín (C) bất kì bằng tổng đại số cường độ của các dòng điện xuyên qua diện tích giới hạn bởi đường cong đó:

n

Hdl

I K k 1

(3.27)

Trong đó, Ik sẽ có dấu dương nếu nó có chiều sao cho đường cảm ứng

từ do nó gây ra cùng chiều với chiều dịch chuyển của đường cong (C), nếu

ngược lại thì Ik sẽ có dấu âm.

Ý nghĩa của định lý

Trong điện trường tĩnh,

Edl

 0 , các đường sức điện trường là những

đường cong không kín, điện trường là trường thế.

n

Trong từ trường tích phân

Hdl

I K nói chung là không khác không

k 1

nên từ trường không phải là trường thế mà là một trường xoáy.

Chú ý

Trong tổng các dòng điện, không cần chú ý đến những dòng điện không xuyên qua diện tích giới hạn bởi đường cong kín.

Nếu đường cong kín bao quanh dòng điện nhiều lần thì phải chú ý đến dấu của cường độ dòng điện đối với mỗi vòng dịch chuyển trên đường cong đó.

3.4.3. Ứng dụng của định lý Amper về dòng toàn phần

Định lý Amper về dòng điện toàn phần cho phép ta tính được một cách nhanh chóng cường độ từ trường H và cảm ứng từ B của một số dòng điện.

a. Cường độ từ trường tại một điểm bên trong dây điện hình xuyến

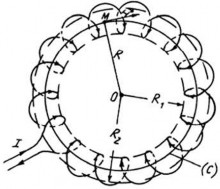
Xét một đây điện hình xuyến gồm n vòng dây có dòng điện I chạy qua như hình vẽ. Do tính đối xứng của vòng dây với tâm điểm O nên vectơ cường độ từ trường H tại mọi điểm trên đường tròn (C) tâm O bán kính R là như nhau.

Áp dụng định lý Amper về dòng toàn phần thì cường độ từ trường tại một điểm trên

Hình 4.11. Cuộn dây hình xuyến

đường tròn tâm O bán kính R (R1<R<R2) của cuộn dây hình xuyến có n vòng quấn xít nhau có dòng điện có cường độ I chạy qua là:

Hdl Hdl H dl H 2R NI

C C C

Từ đó ta có:

H N I

2R

(3.28)

Cảm ứng từ B là:

B 

0 2R I

(3.29)

b. Cường độ từ trường tại một điểm bên trong ống dây thẳng dài vô hạn mang dòng điện.

Từ biểu thức cường độ từ trường của cuộn dây hình xuyến có các bán

kính vô cùng lớn

R1 R2 

ta có thể suy ra cường độ từ trường tại mọi điểm

bên trong ống dây thẳng dài vô hạn đều bằng nhau và bằng:

H N I

2R

Lại có:

N n

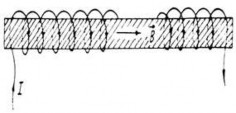
Hình 3.12. Ống dây thẳng dài vô hạn

2R 0

với no là số vòng dây trên một đơn vị dài của ống dây.

Vậy:

H no I

B ono I

(3.30)

Chú ý:Trong thực tế những ống dây có chiều dài lơn hơn mười lần đường kính của nó đều có thể coi gần đúng là ống dây dài vô hạn và có thể coi từ trường trong nó là đều.

3.5. TÁC DỤNG CỦA TỪ TRƯỜNG LÊN DÒNG ĐIỆN

3.5.1. Tác dụng của từ trường lên một phần tử dòng điện

Theo định luật Amper, nếu đặt một phần tử dòng điện Idl tại một điểm M trong từ trường có cảm ứng từ B thì phần tử đó sẽ chịu tác dụng của một lực từ:

dF Idl B

lực này gọi là lực Amper.

Đặc điểm của lực Amper:

 Có phương vuông góc với mặt phẳng chứa Idl và B .

(3.31)

 Có chiều sao cho 3 vectơ dl, B, d F theo thứ tự đó lập thành một tam diện thuận.

 Độ lớn: dF I.dl.B.sin(trong đó là góc giữa Idl và B )

Quy tắc xác định chiều của lực Amper

Để xác định phương chiều của lực Amper một cách thuận tiện chúng ta có thể xác định theo qui tắc bàn tay trái:

Đặt bàn tay trái sao cho các đường sức từ xuyên vào lòng bàn tay, dòng điện đi từ cổ tay đến đầu các ngón tay, thì chiều của ngón tay cái choãi ra chỉ chiều của lực từ.

3.5.2. Tác dụng tương hỗ giữa hai dòng điện thẳng song song dài vô hạn

Cho hai dòng điện thẳng song song dài vô hạn cách nhau một khoảng d, có cường độ lần lượt là I1 và I2. Vì xung quanh mỗi dòng điện đều có từ trường do nó sinh ra nên dòng điện này nằm trong từ trường của dòng điện kia và hai dòng này có tác dụng lực từ lên nhau.

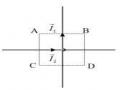
a. Nếu hai dòng điện I1 và I2 cùng chiều

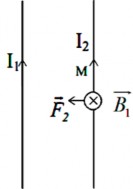
Cảm ứng từ tại điểm M nằm trên I2 do dòng điện I1

gây ra có độ lớn:

B 0 I1

2d

và có phương chiều như Hình 3.13.

(3.32)

Lực từ do từ trường B1 tác dụng lên đoạn dây có chiều dài l của dòng điện I2 là:

Hình 3.13. Tương tác giữa hai dòng điện thẳng

F2 I 2l B

Lực này có đặc điểm:

 Phương vuông góc với mặt phẳng chứa

I2 và

(3.33)

song song cùng chiều

 Chiều hướng về I1

 Độ lớn:

F 0lI1 I 2 2 2d

Như vậy dòng

I1 hút dòng

I2 . Theo định luật III Newton, dòng

I2 hút

dòng

I1 một lực F2 cùng phương ngược chiều với lực

F1 và có độ lớn

F1 F2 .

b. Trường hợp hai dòng điện I1 và I2 ngược chiều:

Lý luận tương tự với trường hợp hai dòng cùng chiều, hai dòng điện ngược chiều thì đẩy nhau.

Vậy:

Hai dòng điện thẳng song song cùng chiều thì hút nhau.

Hai dòng điện thẳng song song ngược chiều thì đẩy nhau.

Lực tương tác giữa hai dòng điện thẳng song song tuân theo công thức:

F Il B

trong đó, F là lực từ tác dụng lên dòng điện I, B là từ trường do dòng điện còn lại gây ra tại các điểm trên dòng điện I.

Chú ý:

Công thức F Il B được áp dụng trong hai trường hợp: tìm lực từ tương tác giữa hai dòng điện thẳng song song, hoặc tìm lực từ do từ trường đều tác dụng lên dòng điện thẳng.

3.5.3. Định nghĩa đơn vị cường độ dòng điện

Trong công thức:

0lI1 I 2

2d

nếu:

I1 I2 I ;

d  1(mét) ;  1 và

F  2.107 N

thì I =1amper.

Vậy Amper là cường độ dòng điện không đổi theo thời gian chạy qua hai dây dẫn thẳng song song, dài vô hạn, có tiết diện nhỏ không đáng kể đặt trong chân không cách nhau 1mét thì gây nên trên mỗi mỗi mét dài của dây

một lực F  2.107 N .

Trong hệ đơn vị SI, Amper là đơn vị thứ tư sau ba đơn vị cơ bản là mét (m), kilogram (kg) và giây (s).

3.5.4. Tác dụng của từ trường đều lên một mạch điện khép kín

Xét một khung dây dẫn kín hình chữ nhật ABCD có các cạnh là a và b. Dòng điện chạy trong khung có cường độ I. Khung được đặt trong từ trường

đều có cảm ứng từ B có phương vuông góc với các cạnh AB, CD. Giả sử khung rất cứng, không bị biến dạng và chỉ có thể quay xung quanh trục đối xứng Δ của nó.

Gọi góc giữa vectơ pháp tuyến n của khung và cảm ứng từ B hợp với nhau một góc .