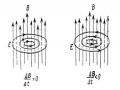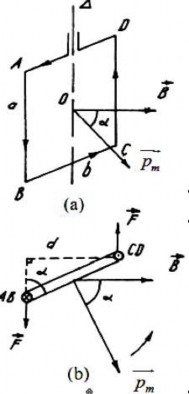
Áp dụng qui tắc bàn tay trái để xác định phương chiều của lực Amper ta có:
Các lực từ tác dụng lên hai cạnh AD và
BC triệt tiêu nhau.
Các lực từ tác dụng lên hai thanh AB và
CD có độ lớn:
F FAB
FCD IaB và
vuông góc với các cạnh này nhưng có chiều ngược nhau. Vì thế chúng tạo thành một ngẫu lực có tác dụng quay khung cho
Có thể bạn quan tâm!
-
Định Luật Amper Về Tương Tác Giữa Hai Phần Tử Dòng Điện -
Định Lý Oxtrogratxki – Gauss Đối Với Từ Trường -
Tác Dụng Của Từ Trường Lên Một Phần Tử Dòng Điện -
K Sẽ Có Dấu Dương Nếu Nó Có Chiều Sao Cho Đường Cảm Ứng Từ Do -
Định Luật Cơ Bản Của Hiện Tượng Cảm Ứng Điện Từ -
Định Luật Cơ Bản Về Hiện Tượng Cảm Ứng Điện Từ
Xem toàn bộ 258 trang tài liệu này.
đến khi
0
hay mặt phẳng của khung
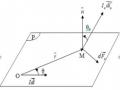
vuông góc với vectơ cảm ứng từ B . Ngẫu lực này có mômen:
M FbsinIBabsinISBsin
M pm Bsin
Hình 3.14. Từ trường tác dụng lên khung dây điện kín
Dạng vectơ:
M Pm B
(3.34)
với Pm IS là vectơ mômen từ của khung.
Ngẫu lực này có tác dụng quay khung cho vectơ mômen từ Pm định
hướng song song với từ trường, khi đó khung ở vị trí cân bằng vì M 0 . Vị trí
cân bằng bền vững của khung là khi 0 tức là
Pm cùng chiều với
Pm . Ngoài
ra, khung còn vị trí cân bằng không bền là khi .
3.6. LỰC TỪ TÁC DỤNG LÊN HẠT MANG ĐIỆN CHUYỂN ĐỘNG
3.6.1. Lực Lorentz
v
Khi phần tử dòng điện Id l nằm trong từ trường sẽ chịu tác dụng của
một lực Amper:
dF Idl B . Mặt khác ta có:
Idl
nq, trong đó: n là số hạt
điện có trong phần tử dòng điện Idl , v là vận tốc chuyển động có hướng của
hạt điện, q là điện tích của mỗi hạt điện.
Vậy, ta có lực Amper có thể viết là:
v
dF
nqB
Khi đó, lực Amper tác dụng lên một hạt điện là:
dF F
n
v
F
qB
(3.35)
Lực
F F
L
tác dụng lên mỗi hạt điện chuyển động trong từ trường gọi
là lực Lorentz.
Từ biểu thức (3.35) thì phương và chiều của lực Lorentz được xác định theo qui tắc bàn tay trái:
Đặt bàn tay trái duỗi thẳng để cho các đường cảm ứng từ (vectơ B ) xuyên vào lòng bàn tay, chiều từ cổ tay đến ngón tay trùng với chiều chuyển
động của hạt (chiều của vectơ vận tốc v ), khi đó ngón tay cái choãi ra 900 chỉ chiều của lực Lorentz nếu hạt mang điện dương (q>0) và chỉ chiều ngược lại nếu hạt mang điện âm (q<0).
3.6.2. Chuyển động của hạt tích điện trong từ trường đều
Ta xét chuyển động của hạt chuyển động với vận tốc v có khối lượng m , điện tích q (q>0) trong từ trường đều, không đổi theo thời gian, có cảm ứng từ B . Vì lực Lorentz luôn vuông góc với vectơ vận tốc v và không thực hiện công nên động năng của hạt không biến đổi do đó độ lớn của vận tốc cũng không đổi mà lực Lorentz chỉ làm cho phương của vectơ vận tốc thay đổi. Như vậy, lực Lorentz đóng vai trò như lực hướng tâm nên:
FL qBv sin
Ta xét hai trường hợp:
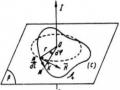
Vận tốc v của hạt vuông góc với cảm ứng từ B
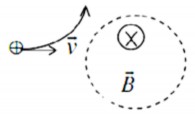
Vì vận tốc v của hạt vuông góc với cảm ứng từ
B nên lực Lorentz làm cho hạt chuyển động trong
mặt phẳng vuông góc với vectơ cảm ứng từ B và có quĩ đạo tròn, bán kính R.
Vậy ta có:
mv
2
FL qBv R
(3.36)
Hình 3.15. Chuyển động của hạt mang điện trong
v
từ trường đều khi B
R mv
qB
(3.37)
Chu kì quay của hạt:
T 2R2m
(3.38)
v qB
Tần số quay:
2
T
qB
m
(3.39)
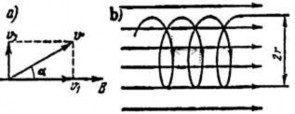
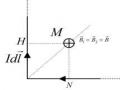
Vectơ v hợp với vectơ B một góc
Phân tích vectơ v thành hai
thành phần: thành phần vvuông
v,
góc với B và thành phần
vH song
Hình 3.16. Chuyển động của hạt mang
song với B .
điện trong từ trường đều khi (B)
Khi đó ta có: v vvH .
Thành phần vận tốc v
với bán kính:
làm cho các hạt chuyển động theo quĩ đạo tròn
R mv
qB
Thành phần vận tốc vH
(3.40)
có tác dụng làm cho hạt chuyển động theo
phương của cảm ứng từ B với vận tốc
vH . Vậy hạt tham gia đồng thời hai
chuyển động, kết quả là quĩ đạo của hạt là đường xoắn ốc, có bán kính
R mv
qB
và bước của quĩ đạo xoắn ốc bằng
h vH T .
3.7. CÔNG CỦA LỰC TỪ
Khi dòng điện đặt trong từ trường thì từ trường tác dụng lực lên dòng điện. Nếu dòng điện đặt tự do thì lực từ có thể làm dịch chuyển dòng điện. Điều đó chứng tỏ lực từ đã sinh công.
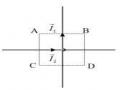
Để tìm công của lực từ, ta xét một đoạn mạch như Hình 3.17. Thanh kim loại AB có thể trượt trên hai thanh kim loại đặt song song và luôn song song với CD. Đặt thí nghiệm trên trong môi trường có từ trường đều có vectơ cảm ứng từ B có phương và chiều như hình vẽ.
Gọi I là cường độ dòng điện chạy trong mạch, l là chiều dài của thanh
AB khi đó lực Amper tác dụng lên thanh có giá trị bằng:
F IBl (3.41)
Dưới tác dụng của lực này, thanh AB dịch chuyển trên hai thanh day. Giả sử đoạn dịch chuyển là dx. Công của lực Amper thực hiện được là:
dA Fdx IlBdx (3.42)
Mặt khác:
ldx dS
dA IBdS (3.43)
Lại có:
BdS d
là từ thông gửi qua diện tích dS .
Vậy:
dA IBdS (3.44)
Nếu thanh AB dịch chuyển từ vị trí 1 đến vị trí 2 và dòng điện chạy trên mạch là không đổi thì:
2 2
A I dI dI(3.45)
1 1
trong đó là từ thông gửi qua diện tích bị quét.
Gọi 1 là từ thông gứi qua diện tích mạch điện ứng với vị trí 1 của AB.
2 là từ thông gửi qua diện tích mạch điện ứng với vị trí 2 của AB. Ta được:
1 2 là độ biến thiên từ thông gửi qua diện tích mạch điện.
A II (2 1 )
(3.46)
Thực tế đã chứng minh được công thức (3.46) đúng cho mọi mạch điện bất kỳ. Vậy ta có thể phát biểu:
Công của lực từ trong quá trình làm dịch chuyển một mạch điện bất kì bằng tích số giữa cường độ dòng điện chạy trong mạch và độ biến thiên từ thông gửi qua diện tích của mạch đó.
Bài toán 5:
Một khung dây dẫn điện hình tròn bán kính r 5cm treo trong từ trường đều B 0, 5T sao cho mặt phẳng khung vuông góc với các đường sức của từ trường. Biết cường độ dòng điện chạy trong khung dây I 2A. Tính:
a. Từ thông gửi qua diện tích giới hạn bởi mặt khung.
b. Công cần thiết để quay mặt khung một góc 2
quanh trục đi qua
đường kính của khung.
Giải:
a. Từ thông gửi qua diện tích giới hạn bởi mặt khung: Theo định nghĩa từ thông ta có:
B. dS B.dS cos
S S
Theo bài ra ta có: 0 , từ trường đều và diện tích S của khung không đổi nên ta có:
BdS B.S 0,5.3,14.(5.102 )2 16.104 Wb
S
b. Công cần thiết để quay mặt khung một góc 2
quanh trục đi qua đường
kính của khung chính bằng công cần thiết để thắng công của lực từ:
ở đây ' 0
vì '
2
A'
.
A I (') 2 0 16.104
32.104 J
TỔNG KẾT CHƯƠNG 3
1. Định luật Amper
Thực nghiệm chứng tỏ, hai dây dẫn mang dòng điện đặt gần nhau thì chúng có tương tác với nhau. Tương tác của các dây dẫn mang dòng điện chạy qua có bản chất giống như tương tác của các nam châm gọi là tương tác từ của dòng điện.
Tương tác giữa hai phần tử mang dòng điện được xác định bởi định luật Amper:
I dl
(I dl r )
d F o.o o
7
o 4r 3
trong đó là độ từ thẩm của môi trường;
2. Khái niệm từ trường
0 4.10 H / m
Vận dụng thuyết tương tác gần, chúng ta đã giải thích được bản chất của tương tác trên và thừa nhận, xung quanh dòng điện có một môi trường đặc biệt gọi là từ trường. Từ trường có khả năng tác dụng lực lên các dòng điện khác đặt trong nó.
3. Vectơ cảm ứng từ.
Đặc trưng cho từ trường về mặt định lượng (mặt tác dụng lực) tại một điểm M bất kì trong không gian người ta đưa ra một đại lượng vật lý đó là vectơ cảm ứng từ.
Từ trường do phần tử mang dòng điện định luật Biot-Savart-Laplace:
Idl
gây nên được xác định bởi
I dl r
d BM
o.
4r 3
Từ định luật Biot-Savart-Laplace ta có lực từ d F do phần tử dòng điện
I dl tác dụng lên phần tử dòng điện I o dlo xác định bằng công thức:
d F I o dlo d B
4. Vectơ cường độ từ trường:
B
o
H
5. Nguyên lý chồng chất từ trường:
Cảm ứng từ B do một dòng điện gây ra tại điểm M
B d B
Cảm ứng từ B do nhiều dòng điện sinh ra
n
1 2 n i
B B B ... B B
i 1
6. Đường cảm ứng từ
Về phương diện hình học từ trường được mô tả bằng các đường cảm ứng từ. Đường cảm ứng từ là đường cong mà tiếp tuyến tại mọi điểm của nó trùng với phương của vectơ cảm ứng từ tại những điểm ấy, chiều của đường cảm ứng từ là chiều của vectơ cảm ứng từ. Các đường cảm ứng từ không cắt nhau và là các đường cong khép kín.
7. Định lý Ôxtrôgratxki – Gauss đối với từ trường
Định lý Ôxtrôgratxki – Gauss đối với từ trường cho chúng ta cách xác định từ thông gửi qua một mặt kín:
BdS 0
s
Từ thông gửi qua một mặt kín bất kì bằng không.
Định lý Ôxtrôgratxki – Gauss đối với từ trường chứng tỏ đường sức từ là những đường cong khép kín.
8. Định lý Amper về dòng điện toàn phần
Lưu số của vectơ cường độ từ trường dọc theo một vòng của đường cong kín (C) bất kì bằng tổng đại số cường độ của các dòng điện xuyên qua diện tích giới hạn bởi đường cong đó: