Bảng 3.13: Kết quả phương pháp mô phỏng ngẫu nhiên xác định hệ số tối ưu
Hệ số độ lệch sản lượng (βy) | Hàm tổn thất (công thức 2.20) | Hàm tổn thất (công thức 2.24) | Hàm tổn thất (công thức 2.25) | |
0,4 | 0,6 | 1512,615 | 1422,512 | 20,91177 |
Có thể bạn quan tâm!
-
Tiến Trình Cơ Chế Điều Hành Lãi Suất Của Ngân Hàng Nhà Nước Việt Nam -
Lãi Suất Chính Sách Ở Việt Nam Theo Quy Tắc Taylor Với Các Hệ Số Mặc Định Thời Kỳ Năm 2015 - 2016 -
Kiểm Định Tính Bền Vững Của Mô Hình Var Có Độ Trễ Là 1 -
Tính Chủ Động Của Cơ Chế Điều Hành Lãi Suất -
Xây Dựng Một Khuôn Khổ Chính Sách Tiền Tệ Định Hình Rò Nét -
Hoàn Thiện Cơ Sở Pháp Lý Tạo Điều Kiện Thuận Lợi Cho Việc Thực Hiện Chính Sách Tiền Tệ
Xem toàn bộ 260 trang tài liệu này.
Nguồn: tác giả tính toán từ phần mềm Eviews 6.0
Bảng 3.14: Kết quả phương pháp mô phỏng ngẫu nhiên đối với các hệ số cố định của quy tắc Taylor
Hệ số độ lệch sản lượng | Hàm tổn thất (công thức 2.20) | Hàm tổn thất (công thức 2.24) | Hàm tổn thất (công thức 2.25) | |
0,5 | 0,5 | 1533,812 | 1422,755 | 20,92308 |
0,5 | 1 | 1543,123 | 1423,597 | 20,93271 |
0,5 | 1,5 | 1559,628 | 1424,840 | 20,94713 |
1 | 0,5 | 2070,473 | 1423,017 | 20,94140 |
1 | 1 | 2099,329 | 1423,449 | 20,92931 |
1 | 1,5 | 2126,669 | 1423,932 | 20,93454 |
1,5 | 0,5 | 3338,816 | 1423,836 | 20,92691 |
1,5 | 1 | 3378,685 | 1423,749 | 20,93809 |
1,5 | 1,5 | 3421,649 | 1423,552 | 20,92717 |
Nguồn: tác giả tính toán từ phần mềm Eviews 6.0
Ghi chú: Hệ số cố định là hệ số có giá trị là bội số của 0,5 áp dụng vào quy tắc Taylor (1993) theo công thức (1.4).
So sánh giá trị hàm tổn thất có được từ phương pháp mô phỏng ngẫu nhiên và tính toán từ số liệu thực tế ở Việt Nam giai đoạn 2000Q1 – 2015Q4 ta có kết quả trình bày ở Bảng 3.15 bên dưới.
Một số nhận xét từ kết quả ở các Bảng 3.13 đến Bảng 3.15:
Kết quả từ phương pháp mô phỏng ngẫu nhiên tương thích với kết quả kiểm tra qua số liệu thực tế các hệ số lạm phát và hệ số độ lệch sản lượng tối ưu đối với quy tắc Taylor gốc (1993) với mục tiêu tối thiểu hóa hàm tổn thất của NHNN.
Bảng 3.15: So sánh giá trị hàm tổn thất từ phương pháp mô phỏng ngẫu nhiên và từ số liệu thực tế
Hệ số độ lệch sản lượng | Hàm tổn thất (công thức 2.20) (*) | |||
Dữ liệu từ phương pháp mô phỏng (a) | Dữ liệu thực tế (b) | Chênh lệch (a – b) | ||
Hệ số tối ưu | ||||
0,4 | 0,6 | 1512,615 | 1749,517 | -236,902 |
Hệ số cố định | ||||
0,5 | 0,5 | 1533,812 | 1762,080 | -228,268 |
0,5 | 1 | 1543,123 | 1824,164 | -281,041 |
0,5 | 1,5 | 1559,628 | 1914,161 | -354,533 |
1 | 0,5 | 2070,473 | 3447,850 | -1377,377 |
1 | 1 | 2099,329 | 3479,576 | -1380,247 |
1 | 1,5 | 2126,669 | 3539,214 | -1412,545 |
1,5 | 0,5 | 3338,816 | 6314,391 | -2975,575 |
1,5 | 1 | 3378,685 | 6322,515 | -2943,830 |
1,5 | 1,5 | 3421,649 | 6358,552 | -2936,903 |
Nguồn: tác giả tính toán
Ghi chú: (*): giá trị hàm tổn thất của dữ liệu thực tế theo công thức (2.24) là 1589,205 và công thức (2.25) là 24,8313 không đổi khi thay đổi hệ số độ lệch lạm phát (βπ) và hệ số độ lệch sản lượng (βy) với giá trị lạm phát mục tiêu đã xác định trước.
Kết quả mô phỏng từ Bảng 3.14 cho thấy khi nâng hệ số lạm phát lên với bước nhảy là 0,5, giá trị hàm tổn thất theo công thức (2.20) tăng mạnh do thành tố độ lệch lãi suất (iTAYLOR – it) tăng. Giữ nguyên hệ số lạm phát, tăng hệ số độ lệch sản lượng cũng làm cho giá trị hàm tổn thất tăng nhưng không đáng kể. Khi thay đổi giá trị của các hệ số, giá trị hàm tổn thất theo công thức (2.24) và (2.25) thay đổi nhưng không nhiều. Kết quả mô phỏng và tính toán số liệu thực tế khẳng định trong các cặp hệ số cố định (βπ , βy) thì cặp hệ số (0,5; 0,5) có giá trị hàm tổn thất nhỏ nhất.
Giá trị hàm tổn thất tính theo phương pháp mô phỏng ứng dụng quy tắc Taylor và các mô hình dự báo lạm phát và sản lượng cho giá trị hàm tổn thất nhỏ hơn giá trị hàm tổn thất thực tế.
Kết quả phương pháp mô phỏng ngẫu nhiên cho thấy hệ số lạm phát (0,4) và hệ số độ lệch sản lượng (0,6) là tối ưu trong điều kiện kinh tế Việt Nam giai đoạn 2000Q1 – 2015Q4.
Việc ứng dụng quy tắc Taylor trong chính sách lãi suất của NHNN giúp giảm giá trị hàm tổn thất. Việc xác định đúng các hệ số của quy tắc Taylor có ý nghĩa quan trọng, đặc biệt là hệ số độ lệch lạm phát (βπ).
Kết luận từ phương pháp mô phỏng ngẫu nhiên tính giá trị hàm tổn thất:
Kết quả từ phương pháp mô phỏng ngẫu nhiên theo mô hình New Keynesian cho thấy khi ứng dụng quy tắc Taylor và các mô hình dự báo lạm phát và sản lượng cho kết quả giá trị hàm tổn thất mô phỏng nhỏ hơn giá trị hàm tổn thất thực tế. Qua đó cho thấy Việt Nam có thể ứng dụng quy tắc Taylor vào quá trình ra quyết định về LSCS là hoàn toàn khả thi với minh chứng là giá trị hàm tổn thất nhỏ đi. Áp dụng phương pháp mô phỏng ngẫu nhiên với quy tắc Taylor và các mô hình dự báo tỉ lệ lạm phát và độ lệch sản lượng ở Việt Nam thời kỳ 2000Q1 – 2015Q4 với LSCS là TLS được giá trị tối ưu của hệ số độ lệch lạm phát là 0,4 và hệ số độ lệch sản lượng là 0,6.
3.2.2.5 Quy tắc Taylor với tổng phương tiện thanh toán M2
Như đã đề cập ở chương 2, hệ phương trình đồng thời (2.27) biểu diễn quan hệ giữa quy tắc Taylor với tỉ lệ tăng M2 như sau:
Giải hệ phương trình (2.27) bằng phần mềm Eviews 6.0 trong giai đoạn 2000Q1 – 2015Q4 theo phương pháp Two-Stage Least Square (TSLS), và các biến πt là tỉ lệ lạm phát 4 quý liền kề (INF), yt là độ lệch sản lượng (OGAP), ∆M là tỉ lệ tăng M2, it là biến TLS, ta có phương trình kinh tế lượng giữa ∆M và it như sau:
∆M = 33,47 - 0.58*it (3.3)
Sai số (5,97) (0,63)
Giá trị p (0,00) (0,35)
Tương ứng với phương trình (3.3), quy tắc Taylor được hồi qui theo hệ phương trình (2.27) được biểu diễn như sau:
(3.4) Sai số (0,33) (0,03) (0,27)
Giá trị p (0,00) (0,00) (0,0051)
Kết quả hồi qui được trình bày ở Phụ lục 15.
Phương trình (3.3) cho thấy khi NHNN quyết định tăng TLS lên 1 đơn vị thì tổng phương tiện thanh toán M2 giảm 0,58% và ngược lại. Hệ số hồi qui của TLS ở mô hình (3.3) âm là phù hợp với lý thuyết tiền tệ khi lãi suất tăng thì tổng phương tiện thanh toán giảm và ngược lại.
Phương trình (3.4) là kết quả hồi qui mô hình kinh tế lượng của quy tắc Taylor (2.2) với ba biến TLS, INF, OGAP theo phương pháp OLS cho biết hệ số lạm phát là 0,37 và hệ số độ lệch sản lượng là 0,78 thời kỳ 2000Q1 – 2015Q4.
3.2.2.6 Dự báo lãi suất chính sách theo mô hình hồi qui quy tắc Taylor
Một số giả định làm cơ sở để dự báo:
NHNN giữ nguyên mức TLS ngắn hạn năm 2016 không thay đổi so với năm 2015 là 5,5%/năm. Số liệu năm 2016 về tỉ lệ lạm phát và độ lệch sản lượng được dự báo từ mô hình dự báo (2.4) và (2.5). Tỉ lệ lạm phát mục tiêu (CPI) 5%/năm và LSTN là 3,61%/năm.
Dự báo tỉ lệ lạm phát quý năm 2016
Mô hình dự báo lạm phát (2.4) theo Rudebusch và Svensson (1998) được hồi quy với dữ liệu kinh tế vĩ mô thời kỳ 2000Q1 – 2015Q4 và giả định dự báo ở trên bằng phần mềm Eviews 6.0 cho kết quả như sau:
INFt+1 = 1,7016*INFt – 0,9706*INFt-1 + 0,0138*INFt-2 + 0,2244*INFt-3 + 0,4002*OGAPt (3.5)
Với INFt là biến lạm phát (πt) và OGAPt là biến độ lệch sản lượng (yt)
Dự báo với mô hình (3.5), ta có tỉ lệ lạm phát quý 1 năm 2016 là 1,32%/năm, quý 2: 1,84%, quý 3: 1,81% và quý 4: 1,40%.
Dự báo độ lệch sản lượng quý năm 2016
Hồi quy mô hình dự báo độ lệch sản lượng (2.5) theo Svensson (1996) và Rudebusch và Svensson (1998) với dữ liệu kinh tế vĩ mô thời kỳ 2000Q1 – 2015Q4 và giả định dự báo ở trên vào mô hình và tính toán với phần mềm Eviews 6.0, ta có mô hình sau:
OGAPt+1 = 0,819*OGAPt – 0,1225*OGAPt-1 – 0,00058*(TLSt-INFt) (3.6)
Dự báo với mô hình (3.6), ta có độ lệch sản lượng quý 1 năm 2016 là 0,15, quý 2: 0,09, quý 3: 0,06 và quý 4: 0,03.
Bảng 3.16: Dự báo kinh tế vĩ mô năm 2016
Trần lãi suất huy động (%/năm) | Tỉ lệ lạm phát 4 quý liền kề (%/năm) | Độ lệch sản lượng | |
2016Q1 | 5,5 | 1,32 | 0,15 |
2016Q2 | 5,5 | 1,84 | 0,09 |
2016Q3 | 5,5 | 1,81 | 0,06 |
2016Q4 | 5,5 | 1,40 | 0,03 |
Nguồn: tác giả tính toán từ phần mềm Eviews 6.0
Áp dụng mô hình Taylor dạng (1.27)
với phương trình làm phẳng lãi suất ở độ trễ là 1 (n=1, p=1) phù hợp với nền kinh tế Việt Nam thời kỳ 2000Q1 – 2015Q4 theo phương pháp hồi qui OLS, sử dụng chức năng dự báo bằng phần mềm Eviews 6.0 với các biến TLS_DB, INF_DB và OGAP_DB trong thời kỳ 2000Q1 – 2016Q4, ta có kết quả dự báo như sau:
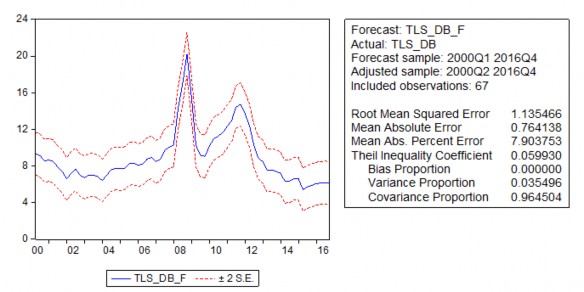
Hình 3.3: Kết quả dự báo TLS thời kỳ 2000Q1 – 2016Q4
Nguồn: tác giả tính toán kết quả dự báo từ phần mềm Evews 6.0
Với hệ số Theil là 0,05993 rất gần với 0 và RMSE là 1,135466 rất nhỏ, do vậy kết quả dự báo có độ tin cậy cao. Kết quả dự báo TLS quý 1 năm 2016 là 6,07%/năm, quý 2: 6,13%, quý 3: 6,19% và quý 4: 6,14%.
Kết quả dự báo cho thấy trong năm 2016, TLS tính theo quy tắc Taylor bằng các mô hình kinh tế lượng là khoảng 6%/năm. Đến tháng 9 năm 2016, NHNN vẫn giữ mức TLS huy động cho các khoảng tiền gửi VND dưới 6 tháng là 5,5%/năm cho thấy NHNN có khả năng vẫn đang nới lỏng lãi suất có kiểm soát nhằm thực hiện mục tiêu tăng trưởng kinh tế ổn định và vẫn kiểm soát tỉ lệ lạm phát.
Kết luận về công tác phân tích thực trạng chính sách lãi suất của NHNN bằng quy tắc Taylor
Qua phân tích thực trạng chính sách lãi suất của NHNN bằng phương pháp tính toán thông thường và phân tích kinh tế lượng cho thấy công cụ TLS của NHNN phù hợp với quy tắc Taylor gốc (1993) và quy tắc Taylor dạng làm phẳng lãi suất sử dụng biến trễ bằng 1. Đồng thời tác giả cũng dùng phương pháp vector tự hồi qui (VAR) để đạt được mô hình có độ trễ tối ưu là 1 với các biến TLS, INF và OGAP. Thông qua phân tích hàm phản ứng đẩy và phân rã phương sai có thể thấy được tác động giữa hai biến lạm phát và trần lãi suất là rất mạnh trong ngắn hạn (từ một đến
ba quý). Điều này cho thấy NHNN đã và đang sử dụng công cụ TLS là phù hợp để đạt được mục tiêu kiểm soát lạm phát trong ngắn hạn.
Căn cứ vào đặc điểm và tính chất của cơ chế điều hành lãi suất của NHNN trong quá trình thực thi chính sách lãi suất của NHNN trong thời kỳ năm 2000 – 2015 cùng với kết quả từ công tác phân tích chính sách lãi suất của NHNN bằng quy tắc Taylor, tác giả đưa ra một số nhận xét về thành công và hạn chế của cơ chế điều hành lãi suất của NHNN.
3.3 Thành công và hạn chế của cơ chế điều hành lãi suất của Ngân hàng Nhà nước Việt Nam
3.3.1 Thành công của cơ chế điều hành lãi suất
Trong suốt quá trình đổi mới và phát triển từ năm 1990 đến nay, trải qua các thời kỳ biến động lãi suất cao, đặc biệt là năm 2008 và 2011, NHNN đã vận dụng cơ chế điều hành lãi suất linh hoạt mang lại hiệu quả nhất định trong việc kiềm chế lạm phát, góp phần ổn định và tăng trưởng kinh tế, cụ thể:
+ NHNN đã thành công trong việc điều hành công cụ lãi suất bằng việc áp dụng LSCB và/hoặc TLS ngay tại thời điểm lạm phát tăng cao và điều chỉnh dần trần lãi suất theo biên độ giảm dần của tỉ lệ lạm phát ở hai năm có mức lạm phát cao nhất là 2008 và 2011. Trần lãi suất được áp dụng với các khoản tiền gửi ngắn hạn được vận dụng linh hoạt giúp các NHTM không chạy đua lãi suất để cạnh tranh huy động vốn, đồng thời góp phần giảm lãi suất cho vay giúp các doanh nghiệp tiếp cận vốn dễ dàng hơn. Bên cạnh đó, NHNN cũng điều chỉnh LSTCK và LSTCV cùng nhịp với sự thay đổi của LSCB và/hoặc TLS (Phụ lục 3, 4, 5). Kết quả từ phân tích định lượng chính sách lãi suất của NHNN trong thời kỳ năm 2000 – 2015 minh chứng rò ràng hiệu quả của công cụ TLS qua lăng kính quy tắc Taylor.
+ Tốc độ tăng trưởng kinh tế các năm sau lạm phát năm 2011 là 5,03% (2012), 5,42% (2013) , 5,98% (2014) (Phụ lục 1) cho thấy dấu hiệu phục hồi dần của nền kinh tế Việt Nam trong đó có sự đóng góp của CSTT về kiềm chế lạm phát và ổn định phát triển kinh tế. Việc giảm dần TLS ngắn hạn giúp công chúng hướng đến gửi tiền ở kỳ hạn dài hơn làm cho dòng vốn chảy vào hệ thống ngân hàng ổn định,
góp phần phục vụ cho các kế hoạch sản xuất kinh doanh lâu dài của doanh nghiệp. Việc áp dụng TLSCV từ năm 2012 cho thấy NHNN mong muốn thêm nhiều doanh nghiệp tiếp cận được vốn vay, mở rộng qui mô sản xuất nhằm thúc đẩy tăng trưởng kinh tế.
+ Do lạm phát cao được kiểm soát về cơ bản, giá trị đồng tiền nội tệ dần được ổn định sức mua, đồng thời NHNN áp dụng TLS ngoại tệ (đô la Mỹ) thấp giảm từ 2%/năm trong 2 năm 2011 và 2012 xuống 1,5%/năm (2013), 1%/năm (tháng 3/2014) và 0,75%/năm (tháng 10/2014), và gần đây nhất là 0%/năm (tháng 12/2015)28 đối với tiền gửi của dân cư nên xu hướng cất giữ ngoại tệ và vàng trong dân cư giảm, đồng thời NHNN cũng duy trì sự ổn định của tỉ giá hối đoái giúp cho thị trường ngoại tệ ổn định. Về cơ bản kinh tế vĩ mô được ổn định sau thời kỳ lạm
phát cao.
Bên cạnh các thành công trên, cơ chế điều hành lãi suất của NHNN vẫn còn có các mặt hạn chế cần được nhận diện và khắc phục để hoạt động hiệu quả hơn.
3.3.2 Hạn chế của cơ chế điều hành lãi suất
3.3.2.1 Tính thống nhất của cơ chế điều hành lãi suất
Việc áp dụng nhiều loại lãi suất khác nhau trong thời gian ngắn cho thấy NHNN vẫn đang đi tìm một cơ chế LSCS phù hợp với đặc thù của nền kinh tế Việt Nam. Bên cạnh các loại lãi suất “riêng có” của NHNN như LSTCK và LSTCV, LSCB được qui định trong bộ luật Dân sự 1995 và sửa đổi năm 2005 giới hạn mức lãi suất của các giao dịch vay vốn giữa bên vay và bên cho vay. Tuy nhiên LSCB chỉ được áp dụng tuyệt đối từ tháng 5/2008 đến tháng 3/2011 khi nền kinh tế Việt Nam xảy ra lạm phát cao do tác động từ cuộc khủng hoảng tài chính trên thế giới và NHNN đã không công bố LSCB kể từ tháng 12 năm 2010, thay vào đó là TLS và TLSCV ngắn hạn. Việc thay đổi LSCB, TLS trong thời gian quá ngắn ở năm 2008 và 2012 đã ảnh hưởng đến các hoạt động tiết kiệm và cho vay vốn trong nền kinh tế; và lộ trình lãi suất dường như chưa được quyết định rò ràng. Qua đó có thể nhận xét rằng chính sách lãi suất của NHNN chưa mang tính thống nhất do chưa chọn
28 Số liệu từ Ngân hàng Nhà nước Việt Nam www.sbv.gov.vn