chóng, trong khi đó các xác suất lớn nhất của
b002 và
b002 tăng khi tham số a
![]()
![]()
32N
42N0
![]()
Có thể bạn quan tâm!
-
 Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các
Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các -
 Trung Bình Của Phương Trình Vi Phân Ngẫu Nhiên Với Nhiễu Trắng
Trung Bình Của Phương Trình Vi Phân Ngẫu Nhiên Với Nhiễu Trắng -
 Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Hai Mode
Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Hai Mode -
 Xác Suất Để Hệ Tồn Tại Ở Các Trạng Thái Kiểu Bell
Xác Suất Để Hệ Tồn Tại Ở Các Trạng Thái Kiểu Bell -
 Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 16
Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 16 -
 Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 17
Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 17
Xem toàn bộ 144 trang tài liệu này.
![]()
tăng nhưng chúng chỉ đạt các giá trị tương ứng là 0,310 và 0,306. Điều này có
nghĩa là hệ không thể tạo ra các trạng thái kiểu Bell
![]()
![]()
B
,
0012N
00
![]()
![]()
B
32N
00
![]()
![]()
B
và
42N
. Hơn
nữa, khi tham số a0 tăng, các xác suất cực đại dịch chuyển về phía thời gian bằng không, tức là số lượng các đỉnh xác suất tăng lên trong một khoảng thời gian nhất định. Do đó, tham số a0 liên quan đến thành phần nhiễu cũng là một tham số quan trọng để kiểm tra một cách có hiệu quả việc tạo ra các trạng thái kiểu Bell của hệ. Những kết quả này có thể giải thích rằng sự hiện diện của tham số liên quan đến thành phần nhiễu làm thay đổi giao thoa lượng tử của hệ so với trường hợp tham số này vắng mặt.
Phần trên đã xét các trường hợp khi t 0 cả hai mode đã được giả định ở
các trạng thái chân không
![]() 0
0![]()
![]() 0
0![]() và trạng thái n-photon
và trạng thái n-photon
![]() 1
1![]()
![]() 0
0![]() . Bây giờ chúng
. Bây giờ chúng
![]()
![]()
a b
a b
và
ta xem xét sự tiến triển của hệ khi các mode dao động ban đầu ở các trạng thái
0 1
n-photon
![]()
![]()
![]()
![]()
![]() 1
1![]()
![]() 1
1![]() , tức là
, tức là
0
pq0
| ![]() |
| ![]() , với
, với
p, q 0,1. Do đó, sự
![]()
![]()
a b
a b
a b
tiến triển của các trạng thái ban đầu của hệ được xem xét ở đây có dạng như sau:
![]()
![]() 01t
01t
![]()
![]()
11t
cut cut
c00![]() 0
0![]()
![]()
![]()
01
11
a
a
0
0
b
b
c00![]() 0
0![]()
![]()
![]()
c10![]() 0
0![]()
![]()
![]()
10
10
a
a
1
1
b
b
c00![]() 0
0![]()
![]()
![]()
c10![]() 1
1![]()
![]()
![]()
![]()
01
01
a
a
0
0
b
b
c00![]() 1
1 ![]()
![]()
c00![]() 1
1 ![]()
![]()
![]()
10
00
a
a
1
1
,
.
b
b
c00![]() 1
1![]()
![]()
![]()
(3.18)
Từ đó chúng ta dễ dàng tìm được entropy đan rối như sau:
,
11 00
E t E t
01 10
,
E t E t
2 N 2 N
j
và bkl là:
2 N 2 N
(3.19)
b01b10, b01b10,
b01b10, b01b10,
1 2 2 1
3 4 4 3
(3.20)
b11b00, b11b00, b11b00, b11b00.
0 0
1 2 2 1 3 4 4 3
Điều đáng chú ý là nếu
a0 0
thì hệ đối với các trạng thái ban đầu ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1 1
a b
a b
hoặc gần như tiến triển theo chu kỳ thành các trạng thái kiểu Bell tương
ứng
![]()
![]()
B
,
0012N
![]()
![]()
B
0022N
hoặc
11
![]()
![]()
B
,
12N
11
![]()
B
22N
, với độ tin cậy cao nhưng không tiến triển thành
các trạng thái
01
![]()
![]()
B
,
32N
0142N
hoặc
10
![]()
![]()
B
,
32N
10
![]()
![]()
B
42N
. Điều này trái ngược với sự tiến triển
![]()
![]()
B
0 1
a b
của hệ đối với các trạng thái ban đầu ![]()
![]()
![]()
![]()
hoặc ![]() 1
1![]()
![]() 0
0![]() . Nếu
. Nếu
a0 0 , trạng thái
a b
của hệ là các trạng thái đan rối nhưng hệ không tạo ra các trạng thái kiểu Bell cho cả bốn trạng thái ban đầu. Tất cả các đồ thị đối với sự tiến triển của hệ cho
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0 1
1 1
a b
và
a b
các trạng thái ban đầu đều trùng với các Hình từ 3.5 đến 3.8, vì
vậy để cho ngắn gọn, chúng sẽ không được biểu thị ở đây.
3.2.3. Ảnh hưởng của nhiễu trắng đối với sự hình thành các trạng thái đan rối trong bộ nối phi tuyến tương tác phi tuyến được bơm một mode
Trong phần này chúng tôi sẽ xem xét bộ nối phi tuyến gồm hai dao động tử phi tuyến liên kết phi tuyến với nhau, và một trong hai mode của bộ nối này được kích thích bởi một trường thực tế hơn trong trường hợp độ rộng của trường này được tính đến. Điều này có nghĩa là trường ngoài được giả định phân thành hai thành phần: nhiễu trắng và tất định. Điều thú vị chủ yếu theo quan điểm của chúng tôi là những hệ này có thể thay đổi việc tạo ra các trạng thái đan rối cực đại.
3.2.3.1. Mô hình bộ nối phi tuyến tương tác phi tuyến được bơm một mode
Ở phần này bộ nối gồm hai dao động tử phi tuyến tương tác phi tuyến với nhau và một trong hai dao động tử này được bơm bởi trường ngoài được xem xét. Mô hình này là sự mở rộng mô hình đã trình bày ở mục 3.2.1 cho trường hợp liên kết giữa hai dao động tử là liên kết phi tuyến thay cho liên kết tuyến tính. Mô hình này cũng là sự mở rộng của mô hình ở mục 2.2.1 khi trường ngoài được mô hình hóa bởi nhiễu trắng.
Bằng cách giả sử rằng các tham số liên kết
, lúc đó hệ phương trình
chuyển động của các biên độ xác suất (2.42) được viết lại như sau:
i d cpq(t) 2cpq(t),
![]()
dt 20 02
i d cpq(t) cpq(t),
![]()
(3.21)
dt 12 02
i d cpq(t) 2*cpq(t) *cpq(t).
![]()
dt02
20 12
Từ đó, ta áp dụng phương trình trung bình (3.4) cho các phương trình chuyển động của các biên độ xác suất phức (3.21) với các ma trận hằng M1, M2 và M3 được viết dưới dạng:
0 0
2
0
0 0 2
0 0 0
M1 0 0 0 ,
M 2 0 0 1,
M 3 0 0 0, (3.22)
2* * 0
0 0 0
2 1 0
0 0
khi đó hệ các phương trình chuyển động cho các biên độ xác suất trở thành các phương trình trung bình ngẫu nhiên với dạng sau:
i d cpq(t) 2a cpq(t) a cpq(t) 2cpq(t),
![]()
dt 20 0 20 0 12 0 02
i d cpq(t) a cpq(t) a0 cpq(t) cpq(t),
![]()
![]()
(3.23)
dt 12 0 20 2 12 0 02
i d cpq(t) 2*cpq(t) *cpq(t) 5a0 cpq(t).
![]()
![]()
dt 02 0 20 0 12 2 02
![]()
![]()
![]()
![]()
a b
Giả sử rằng tại thời điểm ban đầu (t = 0), mode a chứa cả hai photon còn mode b không chứa photon nào ( 2 0 ) và tham số liên kết là số thực. Lúc
đó nghiệm của hệ phương trình (3.23) tìm được có dạng như sau:
c20(t) 22 cos5
![]()
5a0 t i sin 5a0 t
![]()
![]()
20 5
0t cos2
2
1,
c20(t) 2
![]()
5a0 t i sin 5a0 t
![]()
![]()
(3.24)
12 5 cos 5 0t cos2 2 1,
![]()
c20(t) 2i 5
5
![]()
5a0 t i sin 5a0 t
![]()
![]()
02 5
sin 0t cos2 2 .
Mặt khác nếu giả sử rằng khi t 0 , mode a chứa một photon và mode b chứa hai
a b
photon ( ![]() 1
1![]()
![]() 2
2![]() ) thì nghiệm của hệ phương trình (3.23) có thể tìm được dưới dạng:
) thì nghiệm của hệ phương trình (3.23) có thể tìm được dưới dạng:
c12(t) 2
![]()
5a0 t i sin 5a0 t
![]()
![]()
20 5 cos 5 0t cos2 2 2,
c12(t) 1
![]()
5a0 t i sin 5a0 t
![]()
![]()
(3.25)
12 5 cos 5 0t cos2 2 4,
![]()
c12(t) i 5
5
![]()
5a0 t i sin 5a0 t
![]()
![]()
02 5
sin 0t cos2 2 ,
còn khi ta giả sử tại thời điểm t 0 , mode a không chứa photon nào còn mode b
a b
chứa cả hai photon ![]() 0
0![]()
![]() 2
2![]() ) thì nghiệm của hệ phương trình (3.23) tìm được có dạng:
) thì nghiệm của hệ phương trình (3.23) tìm được có dạng:
c02(t) 2i 5
![]()
5a0
![]()
![]()
5a0
![]()
20 sin 50t cos
t i sin
t ,
5
2 2
![]()
c02(t) i 5
5t cos 5a0 t i sin 5a0 t ,
![]()
![]()
(3.26)
12 5
sin
0 2
2
![]()
![]()
c02(t) cos 5t cos 5a0 t i sin 5a0 t .
![]()
![]()
02 0 2 2
Từ hệ phương trình (3.26), dễ dàng thấy rằng sự tiến triển của entropy đan rối và
![]()
![]()
![]()
![]()
0 2
a b
các trạng thái kiểu Bell đối với trường hợp trạng thái ban đầu không phụ
thuộc vào tham số liên quan đến thành phần nhiễu a0 . Điều đó chứng tỏ rằng đối
với trạng thái ban đầu mà mode a không chứa photon nào, còn mode b chứa cả hai photon thì nhiễu trắng của trường ngoài bơm vào mode a không làm ảnh hưởng đến sự thăng giáng của hệ được xét. Nghĩa là đối với trường hợp này liên kết của các mode rất bền vững, không bị ảnh hưởng bởi nhiễu trắng của các trường liên kết.
Ta có thể sử dụng các biên độ xác suất tìm được trong các phương trình từ (3.24) và (3.25) để thảo luận về sự tiến triển của entropy đan rối và các xác suất cho sự tồn tại của hệ ở các trạng thái kiểu Bell đối với các giá trị khác nhau của tham số a0 ở phần tiếp theo.
3.2.3.2. Ảnh hưởng của nhiễu trắng đối với sự tạo ra các trạng thái đan rối trong bộ nối tương tác phi tuyến được bơm một mode
E
E
và
Bộ nối được xem xét ở đây tương tự với bộ nối đã khảo sát ở mục 2.2.1, vì vậy, để khảo sát sự tiến triển của hệ khi trường ngoài được mô hình hóa bởi nhiễu trắng, chúng tôi sử dụng công thức (2.56) cho các biên độ xác suất phức tìm được từ
(3.24) đến (3.26). Các entropy đan rối
20
3N
12
3N
được chỉ ra trong Hình 3.9.
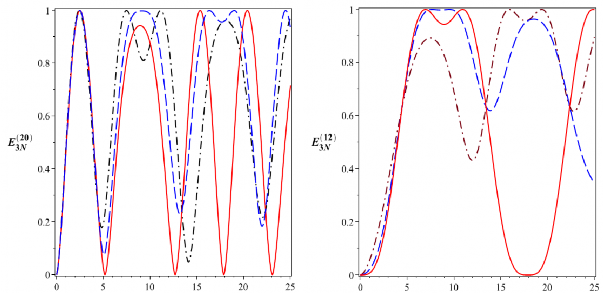
t [10-6s] t [10-6s]
Hình 3.9: Sự tiến triển của các entropy đan rối (đơn vị ebit)
20
E
và
3N
12
E
4
3N
(đơn vị ebit)
trong bộ nối liên kết phi tuyến được bơm một mode với
0 510 rad/s. Đường nét
liền ứng với
a0 0, đường nét gạch ứng với
a 1,25104 rad/s và đường gạch chấm
0
0
ứng với a 2,5104 rad/s
Những kết quả này cho thấy rằng khi tham số
a0 0, entropy đan rối
20
E
3N
trong Hình 3.9 giống kết quả tìm được trong [23].
20
E
3N
12
E
và
3N
thay đổi theo chu
E
E
3N
và
kỳ và đối với các trạng thái kiểu Bell, chúng có giá trị bằng 1 ebit trong khi đối với các trạng thái có thể phân tách, chúng có giá trị bằng 0. Hơn nữa, từ sự tiến
triển của
20
3N
12
3N
cho thấy rằng ngoài cực đại thứ hai của
E20, các cực đại
khác hầu như bằng đơn vị trong khi các cực tiểu hầu như bằng không, tức là hệ này có thể được nghiên cứu như là nguồn của các trạng thái kiểu Bell.
Khi
a0 0 , các entropy đan rối
20
E
3N
12
E
và
3N
cũng thay đổi theo chu kỳ thời
gian. Khi tham số
a0 tăng, cực đại thứ hai của
20
E
3N
cũng tăng đến xấp xỉ bằng
đơn vị và khi đó nó tách thành hai vạch trong khi hai cực đại tiếp theo của
20
E
3N
và hai cực đại đầu tiên của
12
E
3N
giảm dần và nhập lại thành một vạch. Như vậy,
các entropy tiến triển theo thời gian, khi cực đại này bị giảm xuống thì cực đại
khác lại tăng lên xấp xỉ bằng đơn vị theo tham số a0 . Điều đó có nghĩa là hệ
được xét cũng có thể tạo ra các trạng thái kiểu Bell. Ngoài ra, các cực tiểu của
các entropy đều khác không khi a0 tăng. Điều đó có nghĩa là các trạng thái của
hệ trong trường hợp này luôn là trạng thái đan rối. Hơn nữa, cường độ và vị trí
cực đại của các entropy đan rối cũng thay đổi theo thời gian khi tham số a0 tăng.
Bộ nối được xem xét ở đây tương tự với bộ nối đã khảo sát ở mục 2.2.1, vì vậy, để khảo sát sự tạo ra các trạng thái đan rối cực đại của bộ nối này khi trường ngoài được mô hình hóa bởi nhiễu trắng, chúng tôi sẽ sử dụng công thức (2.52) cho các biên độ xác suất phức tìm được từ việc giải hệ phương trình (3.23). Các Hình từ
3.10 đến 3.15 biểu diễn các xác suất cho sự tồn tại của hệ ở các trạng thái kiểu
Bell với các giá trị khác nhau của tham số liên quan đến thành phần nhiễu
a0 .
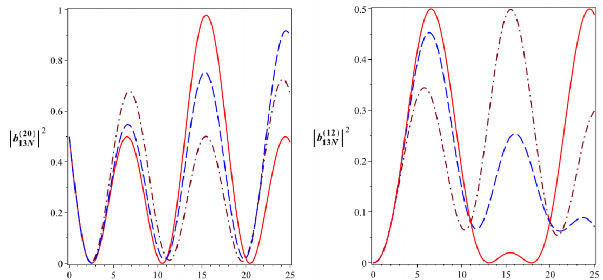
t [10-6s] t [10-6s]
![]()
B
Hình 3.10: Xác suất để hệ tồn tại ở các trạng thái kiểu Bell
2013N
12
![]()
![]()
B
và
13N
với
![]()
4
0 510 rad/s. Đường nét liền ứng với
a0 0, đường nét gạch ứng với
0
0
a 1,25104 rad/s và đường gạch chấm ứng với a 2,5104 rad/s
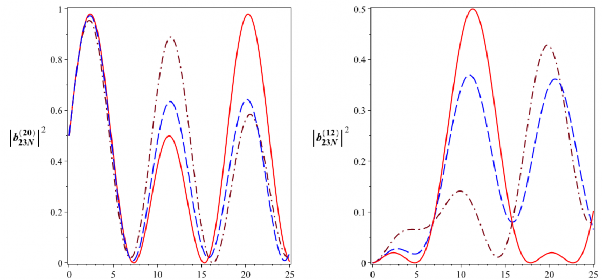
t [10-6s] t [10-6s]
![]()
B
Hình 3.11: Xác suất để hệ tồn tại ở các trạng thái kiểu Bell
2023N
12
![]()
![]()
B
và
23N
với
![]()
4
0 510 rad/s. Đường nét liền ứng với
a0 0, đường nét gạch ứng với
0
0
a 1,25104 rad/s và đường gạch chấm ứng với a 2,5104 rad/s
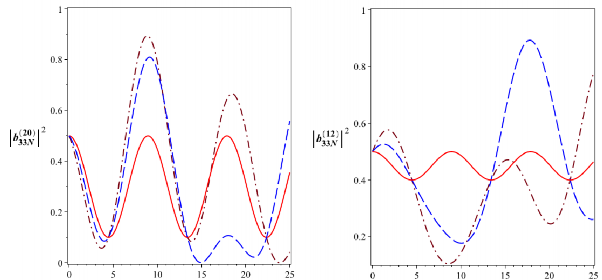
t [10-6s] t [10-6s]
![]()
B
Hình 3.12: Xác suất để hệ tồn tại ở các trạng thái kiểu Bell
2033N
12
![]()
![]()
B
và
33N
với
![]()
4
0 510 rad/s. Đường nét liền ứng với
a0 0, đường nét gạch ứng với
0
0
a 1,25104 rad/s và đường gạch chấm ứng với a 2,5104 rad/s
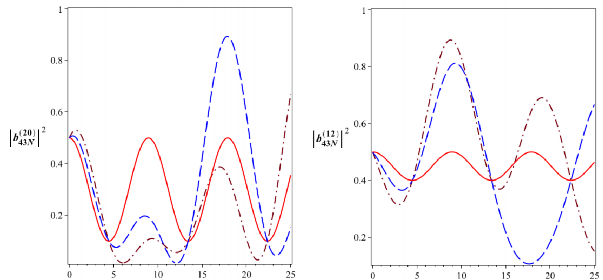
t [10-6s] t [10-6s]
![]()
B
Hình 3.13: Xác suất để hệ tồn tại ở các trạng thái kiểu Bell
2043N
12
![]()
![]()
B
và
43N
với
![]()
4
0 510 rad/s. Đường nét liền ứng với
a0 0, đường nét gạch ứng với
0
0
a 1,25104 rad/s và đường gạch chấm ứng với a 2,5104 rad/s
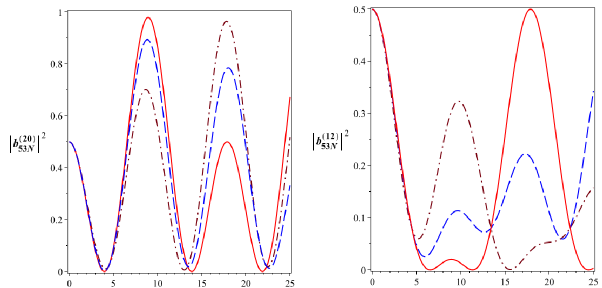
t [10-6s] t [10-6s]
![]()
B
Hình 3.14: Xác suất để hệ tồn tại ở các trạng thái kiểu Bell
2053N
12
![]()
![]()
B
và
53N
với
![]()
4
0 510 rad/s. Đường nét liền ứng với
a0 0, đường nét gạch ứng với
0
0
a 1,25104 rad/s và đường gạch chấm ứng với a 2,5104 rad/s