Xác Suất Để Hệ Tồn Tại Ở Các Trạng Thái Kiểu Bell

t [10-6s] t [10-6s]

B

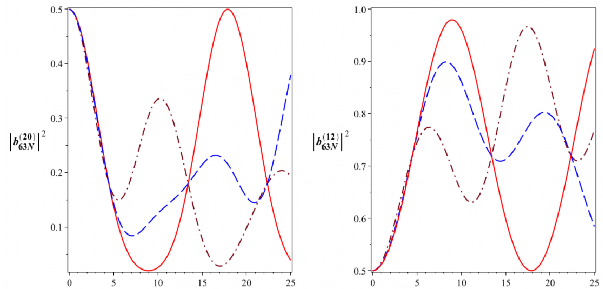
Hình 3.15: Xác suất để hệ tồn tại ở các trạng thái kiểu Bell

2063N

12

B

và

63N

với

4

0  510 rad/s. Đường nét liền ứng với

a0  0, đường nét gạch ứng với

0

0

a 1,25104 rad/s và đường gạch chấm ứng với a  2,5104 rad/s

Khi a0  0, các kết quả thu được (đường nét liền trong các hình vẽ từ 3.10

B

đến 3.15) giống với các kết quả đã tìm được cho trường hợp bộ nối phi tuyến tương tác phi tuyến được bơm một mode bởi trường ngoài ở chương 2. Các giá

trị của cực đại cao nhất của các xác suất tương ứng với các trạng thái

2013N

(Hình

B

3.10),

2023N

(Hình 3.11),

2053N

(Hình 3.14) và

12

B

63N

(Hình 3.15) xấp xỉ bằng đơn

B

vị. Điều này có nghĩa là các trạng thái kiểu Bell được tạo ra, trong khi các trạng thái đan rối cực đại không được tạo ra đối với các trạng thái còn lại. Đối với

trường hợp khi tham số a0 càng tăng, các cực đại lớn nhất của các xác suất gần

bằng đơn vị của các trạng thái kiểu Bell

B

2013N

(Hình. 3.10),

B

2023N

(Hình. 3.11),

B

2053N

(Hình. 3.14) và

12

B

63N

(Hình. 3.15) càng giảm, trong khi các cực đại xác suất

có giá trị từ 0,5 trở xuống lại được tăng cường (từ Hình 3.10 đến 3.15) so với

khi không có mặt của tham số a0 . Do đó, hệ được xem xét có thể tạo ra các trạng

thái kiểu Bell khi giá trị của tham số

a0 là nhỏ, trong khi đối với giá trị

a0 lớn,

các trạng thái đan rối cực đại không thể sinh ra trong hệ. Những kết quả này có thể được giải thích rằng giao thoa lượng tử của hệ được khảo sát trở nên yếu hơn

khi tham số a0 tăng. Ngoài ra có một số xác suất cực tiểu để của hệ luôn lớn hơn

không, nghĩa là các trạng thái này luôn tồn tại ở trạng thái đan rối. Cụ thể, Hình

3.13 cho thấy rằng khi tham số a0 tăng, một số xác suất cực đại của hệ tồn tại ở các

trạng thái

B

20

3

và 20

tăng trong khi các xác suất khác giảm và các xác suất cực tiểu

B

4

để tìm thấy hệ ở các trạng thái này giảm dần về 0. Điều đó có nghĩa là các xác suất để hệ tồn tại ở các trạng thái đan rối này là không ổn định.

Các trạng thái kiểu Bell được tạo ra trong các bộ nối phi tuyến kiểu Kerr nghiên cứu ở đây sẽ được ứng dụng trong các công nghệ như mật mã lượng tử, viễn tải lượng tử hay máy tính lượng tử. Mật mã lượng tử khai thác chính bản chất vật lý của các trạng thái lượng tử. Nó cho phép bảo mật thông tin truyền đi bằng truyền thông quang, qua sợi quang hay qua không gian với thông tin được bảo mật tuyệt đối. Khi viễn tải lượng tử toàn bộ thông tin của qubit được truyền chính xác trong không gian mà không cần sự di chuyển của vật thể mang qubit. Máy tính lượng tử xuất hiện sẽ là thiết bị dùng trực tiếp các trạng thái đan rối lượng tử để thực hiện những phép toán phức tạp của dữ liệu vào nhanh hơn rất nhiều bất kỳ một máy tính hiện tại sử dụng các thuật toán tối ưu nhất hiện nay.

3.3. Kết luận chương 3

Trong chương này, chúng tôi đã nghiên cứu bộ nối phi tuyến gồm hai dao động tử phi tuyến được ghép tuyến tính hoặc phi tuyến với nhau và một hoặc cả hai dao động tử này được bơm bởi các trường ngoài. Các trường ngoài này được mô hình hóa bởi nhiễu trắng.

Bằng cách sử dụng hình thức luận kéo lượng tử phi tuyến, chúng tôi đã chỉ ra rằng sự tiến triển của hệ đối với trường hợp các mode ban đầu ở trạng thái

chân không hoặc ở trạng thái Fock n-photon được khép kín trong một tập hợp hữu hạn của các trạng thái Fock n-photon.

Các kết quả cho thấy rằng khi không có tham số liên quan đến thành phần nhiễu a0, hệ đã tạo ra các trạng thái đan rối cực đại. Hơn nữa, khi tham số a0 có giá trị nhỏ, hệ cũng có thể tạo ra các trạng thái đan rối cực đại so với khi không có mặt của tham số a0. Vì vậy, hệ được xét có thể được xem là nguồn của các trạng thái đan rối cực đại. Ngoài ra, vị trí các cực đại xác suất để hệ tồn tại trong các trạng thái kiểu Bell bị dịch chuyển so với khi không có tham số a0. Kết quả là, tham số a0 liên quan đến thành phần nhiễu là một tham số quan trọng để điều khiển việc tạo ra các trạng thái đan rối cực đại.

Chúng tôi tin rằng mô hình được xét ở đây là thực tế hơn so với mô hình được khảo sát trong trường hợp không có nhiễu trắng, bởi vì cường độ của trường laser được sử dụng trong thực nghiệm luôn chứa một số thành phần thăng giáng.

KẾT LUẬN CHUNG

Khi sự thăng giáng của laser được xét đến trong thực nghiệm, ta sử dụng quá trình ngẫu nhiên để mô hình hóa ánh sáng laser. Khi đó, các phương trình động lực học của hệ được xét trở thành các phương trình vi phân ngẫu nhiên. Việc lấy trung bình các phương trình vi phân ngẫu nhiên này cho ta khả năng phản ánh sự ảnh hưởng của các thăng giáng laser vào các đại lượng nguyên tử được xem xét. Hầu hết các mô hình ngẫu nhiên của laser có đặc điểm chung: laser là một trường điện từ cổ điển và là quá trình ngẫu nhiên Gauss dừng với thời gian tương quan hữu hạn. Việc lấy trung bình giải tích chính xác các phương trình vi phân ngẫu nhiên với nhiễu Gauss có thời gian tương quan hữu hạn là rất khó. Chỉ trường hợp đặc biệt của nhiễu trắng đã được nghiên cứu một cách đầy đủ và thu được nhiều kết quả thú vị. Trong luận án này, chúng tôi đã nghiên cứu việc tạo ra các trạng thái lượng tử có độ đan rối cao trong các bộ nối phi tuyến tương tác tuyến tính hay phi tuyến với nhau được bơm một mode hoặc hai mode bởi trường ngoài đơn sắc, hay được mô hình hóa bởi nhiễu trắng với các điều kiện đầu khác nhau của các phương trình vi phân và đã thu được những kết quả mới, thú vị. Từ đó, chúng tôi rút ra được những kết luận chính sau:

1 0

1 1

và

1. Bằng cách sử dụng hình thức luận kéo lượng tử phi tuyến, đề tài đã chỉ ra rằng sự tiến triển của hệ đối với các bộ nối phi tuyến có thể được khép kín trong một tập hợp hữu hạn các trạng thái n-photon. Cụ thể, sự tiến triển của hệ

được giới hạn trong bốn trạng thái

00,

01,

đối với bộ nối

a b

a b

a b

a b

phi tuyến tương tác tuyến tính, ba trạng thái

02, 12

đối với bộ

a b a b

2 0

và

a b

nối phi tuyến tương tác phi tuyến được bơm một mode và bốn trạng thái

a b a b

2 1

2 0

a b

và

a b

0 2 , 1 2 , đối với bộ nối phi tuyến tương tác phi tuyến

được bơm hai mode.

2. Các bộ nối phi tuyến có thể được xem là nguồn của các trạng thái đan rối cực đại. Các entropy đan rối và trạng thái kiểu Bell của hệ thay đổi một cách đáng kể đối với các điều kiện đầu khác nhau của hệ các phương trình chuyển động của các biên độ xác suất.

3. Hệ được xem xét có thể tạo ra các trạng thái kiểu Bell với độ tin cậy cao đối với trường hợp trường liên kết không có nhiễu. Khi trường liên kết được mô hình hóa bởi nhiễu trắng, xác suất cực đại để hệ tồn tại trong các trạng thái có độ đan rối cao giảm và vị trí cực đại cũng thay đổi nhưng hệ vẫn có thể tạo ra các trạng thái kiểu Bell đối với trường hợp giá trị của tham số liên quan đến

5

thành phần nhiễu a0 là nhỏ, cụ thể a0  10 rad/s đối với bộ nối phi tuyến tương

0

tác tuyến tính được bơm hai mode và a 1,25104 rad/s đối với bộ nối phi tuyến

tương tác phi tuyến được bơm một mode.

4. Tham số liên quan đến thành phần nhiễu a0 là một tham số quan trọng để điều khiển việc tạo ra các trạng thái có độ đan rối cực đại.

5. Mô hình được xem xét khi trường liên kết được mô hình hóa bởi quá trình ngẫu nhiên là thực tế hơn so với mô hình được khảo sát trong trường hợp trường liên kết là đơn sắc, bởi vì cường độ của trường liên kết được sử dụng trong thực nghiệm luôn chứa một số thành phần thăng giáng. Các kết quả thu được là hữu ích để các nhà thực nghiệm lựa chọn mô hình của laser khi nghiên cứu thực nghiệm về thăng giáng lượng tử trong các bộ nối phi tuyến. Nó cũng là nền tảng để nghiên cứu các ứng dụng trong xử lý thông tin lượng tử, truyền thông tin quang và chế tạo máy tính lượng tử.

Trong tương lai, luận án có thể mở rộng nghiên cứu ảnh hưởng của trường liên kết được mô hình hóa bởi nhiễu trắng đối với bộ nối gồm hai dao động tử phi tuyến tương tác phi tuyến với nhau được bơm hai mode bởi trường ngoài. Ngoài ra, luận án hoàn toàn có thể phát triển cho bộ nối gồm ba dao động tử phi tuyến liên kết tuyến tính hoặc phi tuyến với nhau.

Các kết quả nghiên cứu của chúng tôi đã được trình bày trong một số hội thảo khoa học chuyên ngành trong nước và quốc tế. Các kết quả nghiên cứu chính trong luận án cũng đã được công bố trên các tạp chí uy tín trong nước và quốc tế.

CÁC CÔNG TRÌNH KHOA HỌC CỦA TÁC GIẢ ĐÃ CÔNG BỐ

[1] D.Q. Khoa, L.T.T. Oanh, C.V. Lanh, N.T. Dung, N.V. Hoa, “Generation of entangled states by a nonlinear coupler pumped in one mode induced by broadband laser”, Optical and Quantum Electronics 52 (2020) 13(1-12).

[2] L.T.T. Oanh, D.Q. Khoa, C.V. Lanh, H.M. Dong, N.T. Dung, N.T. Thao, N.X. Cuong, “Generation of entangled states by a linear coupling coupler pumped in two modes induced by broadband laser”, Optik - International Journal for Light and Electron Optics 208 (2020) 164028(1-8).

[3] N.T. Anh, L.T.T. Oanh, C.V. Lanh, N.T. Dung, H.M. Dong, D.Q. Khoa, “Broadband laser-driven creation of entangled state for a nonlinear coupling coupler pumped in one mode”, has been accepted for publication in Optical and Quantum Electronics.

[4] D.Q. Khoa, L.T.T. Oanh, C.V. Lanh, N.T. Dung, D.H. Son, “Generation of maximally entangled states by a Kerr-like nonlinear coupler interacting with external fields”, Communications in Physics 3 (2019) 223-240.

[5] L.T.T. Oanh, C.V. Lanh, N.T. Mạnh, D.Q. Khoa, “Entangled state generation in a linear coupling coupler”, Vinh University Journal of Science 49 (2020) 38-45.

[6] L.T.T. Oanh, D.H. Sơn, C.V. Lanh, H.Q. Quy, D.Q. Khoa, “Entangled state generation by a Kerr-like nonlinear coupling couple”, Journal of Military Science and Technology 61 (2019) 170-175.

[7] D.Q. Khoa, L.T.T. Oanh, C.V. Lanh, N.T. Dung, N.V. Hoa, “Finite- dimensional states and entanglement generation”, Tan Trao University Journal of Science 7 (2018) 97-101.

[8] N.T.H. Sang, L.T.T. Oanh, C.V. Lanh, D.Q. Tuan, L.T. Thuy, L.T.T. Binh,

D.Q. Khoa, “Generation of maximally entangled states in pumped nonlinear couplers induced by broadband laser light”, Journal of Military Science and Technology, Special Issue 48A (2017) 122-127.

TÀI LIỆU THAM KHẢO

[1]

A. Einstein, B. Podolsky, B. Rosen (1935), Can quantum-mechanical description of physical reality be considered complete, Phys. Rev, 47, 777.
[2]	A. Luk, V. Perinov, Z. Hradil (1988), Nonstationary Casimir effect in cavities with two resonantly coupled modes, Acta. Phys. Pol. 74, 713.
[3]	M.K. Olsen (2015), Spreading of entanglement and steering along small Bose-Hubbard chains, Phys. Rev. A 92, 033627.
[4]	X.T. Zou, L. Mandel (1990), Photon-antibunching and sub-Poissonian photon statistics, Phys. Rev. A 41, 475.
[5]	L.M. Duan, G. Giedke, J.I. Cirac and P. Zoller (2000), Inseparability Criterion for Continuous Variable Systems, Phys. Rev. Lett. 84, 2722.
[6]	M. Hillery and M. S. Zubairy (2006), Entanglement Conditions for Two- Mode States, Phys. Rev. Lett. 96, 050503.
[7]	C.T. Lee (1990), Higher-order criteria for nonclassical effects in photon statistics, Phys. Rev. A 41, 1721.
[8]	M. Hillery (2000), Quantum Key Distribution with Continuous Variables in Optics, Phys. Rev. A 61, 022309.
[9]	A. Ekert (1991), Quantum cryptography based on Bell’s theorem, Phys. Rev. Lett. 67, 661.
[10]	C.H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, W.K. Wootters (1993), Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels, Phys. Rev. Lett. 70, 1895.
[11]	C.H. Bennett, S.J. Wiesner (1992), Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states, Phys. Rev. Lett. 69, 2881.

Có thể bạn quan tâm!

• Trung Bình Của Phương Trình Vi Phân Ngẫu Nhiên Với Nhiễu Trắng
• Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Hai Mode
• Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến Được Bơm Một Mode
• Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 16
• Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 17
• Ứng dụng lý thuyết quá trình ngẫu nhiên để nghiên cứu thăng giáng lượng tử trong các bộ nối phi tuyến kiểu Kerr - 18

Xem toàn bộ 144 trang tài liệu này.

[12]

M. Stobińska, A.S. Villar, G. Leuchs (2011), Qubit-qubit entanglement dynamics control via external classical pumping and Kerr nonlinearity mediated by a single detuned cavity field powered by two-photon processes, Euro. Phys. Lett. 94, 54002.
[13]	A. Miranowicz, R. Tanaś, S. Kielich, (1990), Generation of discrete superpositions of coherent states in the anharmonic oscillator model, Quant. Opt. 2, 253.
[14]	M. Paprzycka, R. Tanaś (1992), Quantum - optical states in finite - dimensional Hibert space, J. Eur. Opt. Soc. B 4, 331.
[15]	M. Stobińska, H. Jeong, and T. C. Ralph (2007), Violation of Bell’s inequality using classical measurements and nonlinear local operations, Phys. Rev. A 75, 052105.
[16]	H. Wang, X. Gu, Y.X. Liu, A. Miranowicz, F. Nori (2015), Photon blockade in a double-cavity optomechanical system with nonreciprocal coupling, Phys. Rev. A 92, 033806.
[17]	V. Peřinová, A. Lukš, J. Křapelka (2013), Dynamics of nonclassical properties of two-and four-mode Bose-Einstein condensates, J. Phys. B: At. Mol. Opt. Phys. 46, 195301.
[18]	W. Leoński (1996), Quantum and classical dynamics for a pulsed nonlinear oscillator, Physica A 233, 365.
[19]	W. Leoński, A. Kowalewska-Kudłaszyk (2011), Quantum scissors - Finite-dimensional states engineering, Progress in Optics 56, 131.
[20]	A. Miranowicz, W. Leoński (2006), Two-mode optical state truncation and generation of maximally entangled states in pumped nonlinear couplers, J. Phys. B: Atomic, Molecular and Optical Physics, 39, 1683.