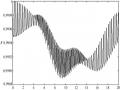
nữa, vị trí cực đại và cực tiểu của các xác suất dịch chuyển về phía thời gian bằng không so với khi β = 0.
Bộ nối phi tuyến được đề cập ở trên còn có nhiều ứng dụng trong các thiết bị quang học như: cảm biến sợi, bộ tách kênh, cổng logic quang học, các máy nén xung, máy thu bán dẫn, chuyển mạch quang.
2.3. Kết luận chương 2
Trong chương này, mô hình bộ nối phi tuyến gồm hai dao động tử phi tuyến liên kết phi tuyến hoặc tuyến tính với nhau và được bơm một mode hoặc hai mode bởi trường kết hợp ngoài đã được thảo luận.
Bằng cách sử dụng hình thức luận kéo lượng tử phi tuyến, sự tiến triển của hệ theo thời gian chỉ là sự tổ hợp hữu hạn các trạng thái lượng tử đã được chỉ ra. Các trạng thái này thay đổi tùy thuộc vào dạng tương tác giữa các mode và giữa các mode với trường kết hợp ngoài.
Các kết quả thu được cho thấy hệ có thể tạo ra các trạng thái đan rối cực đại với độ chính xác cao. Tính hợp lý của các kết quả được khẳng định khi so sánh với các kết quả đạt được trong các công trình trước đó.
Chúng tôi đã mở rộng khảo sát các bài toán đối với các điều kiện đầu khác nhau. Các kết quả chỉ ra rằng, giá trị và vị trí cực đại của các entropy đan rối và các xác suất để hệ tồn tại trong các trạng thái kiểu Bell thay đổi một cách đáng kể đối với các điều kiện đầu khác nhau của các phương trình chuyển động của biên độ xác suất, cũng như với các giá trị khác nhau của các tham số liên kết.
Chương 3
Có thể bạn quan tâm!
-
 Độ Tin Cậy Của Trạng Thái Cắt Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến
Độ Tin Cậy Của Trạng Thái Cắt Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến -
 Xác Suất Để Hệ Tồn Tại Trong Các Trạng Thái Kiểu Bell
Xác Suất Để Hệ Tồn Tại Trong Các Trạng Thái Kiểu Bell -
 Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các
Sự Tiến Triển Của Entropy Đan Rối (Đơn Vị Ebit) Của Trạng Thái Cắt Đối Với Các -
 Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Hai Mode
Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Tuyến Tính Được Bơm Hai Mode -
 Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến Được Bơm Một Mode
Ảnh Hưởng Của Nhiễu Trắng Đối Với Sự Hình Thành Các Trạng Thái Đan Rối Trong Bộ Nối Phi Tuyến Tương Tác Phi Tuyến Được Bơm Một Mode -
 Xác Suất Để Hệ Tồn Tại Ở Các Trạng Thái Kiểu Bell
Xác Suất Để Hệ Tồn Tại Ở Các Trạng Thái Kiểu Bell
Xem toàn bộ 144 trang tài liệu này.
ẢNH HƯỞNG CỦA NHIỄU TRẮNG ĐỐI VỚI SỰ HÌNH THÀNH TRẠNG THÁI ĐAN RỐI CỰC ĐẠI TRONG BỘ NỐI PHI TUYẾN KIỂU KERR
Một trong những đặc điểm nổi bật của laser là tính đơn sắc cao. Trong hầu hết các công trình đã nghiên cứu trước đây về bộ nối phi tuyến, người ta cho rằng ánh sáng laser là đơn sắc. Ở chương này, chúng tôi xem xét ảnh hưởng của nhiễu trắng đối với khả năng tạo ra các trạng thái lượng tử có độ đan rối cao trong các bộ nối phi tuyến tương tác tuyến tính hay phi tuyến với nhau và được bơm một mode hoặc hai mode bởi trường ngoài.
3.1. Trung bình của phương trình vi phân ngẫu nhiên với nhiễu trắng
Trong bức tranh Heisenberg, các phương trình thu được đối với các biến động lực học là tuyến tính, do đó có thể dễ dàng thu được các phương trình cho các đại lượng trung bình tương ứng bằng cách sử dụng các kết quả quen thuộc từ lý thuyết các quá trình ngẫu nhiên [44, 52, 110, 111]. Đối với các vấn đề được xem xét ở đây, chúng tôi giả sử rằng trường laser được tách thành hai thành phần:
0 t , (3.1)
trong đó 0 là thành phần kết hợp tất định của trường và quá trình ngẫu nhiên
t
được đặc trưng bởi nhiễu trắng dưới dạng sau:
![]()
![]()
t*t
a t t' , (3.2)
0
trong đó: a0 là tham số liên quan tới thành phần nhiễu, dấu ngoặc kép biểu thị giá trị trung bình trên toàn bộ các quá trình t [44, 52]. Lúc đó, dạng tổng quát của các phương trình động lực học đối với hệ được xem xét được viết như sau:
dQ M
![]()
t M
* tM
Q , (3.3)
dt 1 2 3
ở đây Q là hàm véctơ theo thời gian và M1, M2 và M3 là các ma trận hằng.
![]()
![]()
Như đã biết từ lý thuyết quá trình ngẫu nhiên đã được trình bày ở chương một, hàm Q thỏa mãn phương trình trung bình sau [44, 52, 68]:
d QM
![]()
a0 M
![]()
, M Q, (3.4)
dt 1 2
2 3
trong đó M 2, M 3là hệ thức phản giao hoán của M2 và M3.
3.2. Các trạng thái có độ đan rối cực đại tạo ra trong bộ nối phi tuyến kiểu Kerr khi trường laser được mô hình hóa bởi quá trình ngẫu nhiên
3.2.1. Ảnh hưởng của nhiễu trắng đối với sự hình thành các trạng thái đan rối trong bộ nối phi tuyến tương tác tuyến tính được bơm một mode
Mục tiêu ở đây là xem xét ảnh hưởng của nhiễu trường ngoài và trường liên kết đối với việc tạo ra các trạng thái đan rối cực đại trong bộ nối phi tuyến Kerr, bao gồm hai dao động tử phi tuyến lượng tử. Các dao động tử này được ghép tuyến tính với nhau và một trong số chúng được bơm bởi trường cổ điển bên ngoài, được giả sử chia thành hai thành phần: thành phần kết hợp và thành phần nhiễu trắng. Hơn nữa, nghiệm giải tích của phương trình vi phân ngẫu nhiên của biên độ xác suất mô tả động lực học của hệ sẽ được rút ra cũng như biểu diễn bằng đồ thị và so sánh chúng với các kết quả thu được trước đó trong tài liệu.
3.2.1.1. Mô hình bộ nối phi tuyến tương tác tuyến tính được bơm một mode
Mô hình bộ nối phi tuyến tương tác tuyến tính được bơm một mode được xét ở đây là sự mở rộng mô hình đã trình bày ở mục 2.1.1.1 cho trường hợp các trường liên kết được mô hình hóa bởi nhiễu trắng, tức là trường liên kết được giả thiết tách thành hai thành phần là phần kết hợp và nhiễu trắng.
Ta giả sử rằng các tham số liên kết và là bằng nhau, khi đó hệ phương trình chuyển động của các biên độ xác suất (2.13) trở thành hệ phương trình có dạng sau:
i d cij (t) *cij (t),
![]()
dt 00 10
i d cij (t) *cij (t) *cij (t),
![]()
dt 01
10 11
i d cij (t) cij (t) cij (t),
![]()
(3.5)
dt 10
01 00
i d cij (t) cij (t).
![]()
dt 11 01
Bằng cách áp dụng phương trình trung bình (3.4) cho hệ phương trình chuyển động của các biên độ xác suất (3.5) trong đó các ma trận M1, M2 và M3 có dạng như sau:
0
0
0 0
M1
*
0
0
0
0
* *
0 0 ,
0 0
0 0
M 2 1 1
0 0
0 0
0 0,
0
0
M 3 0
0 1 0
0 1 1
0 0 0
, (3.6)
0 0
0
0
0 0
0 1
0 0
0 0
0 0
Để cho gọn, từ đây trở đi dấu ngoặc kép biểu thị giá trị trung bình đã được bỏ qua. Khi đó, ta thu được các phương trình chuyển động cho trung bình ngẫu nhiên của các biên độ xác suất có dạng:
i d cij(t) a0cijt a0cijt *cij(t),
![]()
![]()
![]()
dt00
2 00
2 01
0 10
i d cij(t) a0cijt a cijt *cij(t) *cij(t),
![]()
![]()
dt01
2 00
0 01
0 10
0 11
d ijijijij
a0 ij
![]()
(3.7)
i c (t) c (t) c (t) a c dt 10 0 00 0 01 0 10
t c (t), 211
i d cij(t) cij(t) a0 cij(t) a0 cij(t).
![]()
![]()
![]()
dt 11
0 01
210
211
![]()
![]()
a b
Hơn nữa, giả sử rằng cả hai mode ban đầu ở trạng thái chân không | 0 | 0 và tham
số liên kết là số thực, ta tìm được nghiệm của các biên độ xác suất phức
c
mn
ij t, m, n 0,1. có dạng:
1
3ia0t
i0t
i i0t
i
![]()
![]()
c 00 (t) e
![]()
4 e 2
cos x t sin x t e 2 cos x t sin x t ,
00 2
i
3ia0t
1 5 1
i0ti0t
2 5 2
![]()
c 00 (t) e
4 e 2
sin x t e
2 sin x t,
01
i
5
3ia0t
i0 t
1 2
i0 t
(3.8)
c 00 (t) e
4 e 2
sin x t e
2 sin x t,
10 ![]() 5
5
1
3ia0 t
1
i0ti
2
i0 t
i
c 00 (t) e
![]()
![]()
4 e 2
cos x t sin x t e
1
1
![]()
2 cos x t sin x t ,
2
11 2
5
2 5
trong đó
x1
5 a
![]()
4 0
20
và
x2
5 a
![]()
4 0
20 .
Có thể dễ dàng thấy rằng khi không có mặt của tham số liên quan đến thành phần nhiễu a0 0, kết quả của chúng tôi giống với kết quả thu được trong [20].
Mặt khác, khi giả sử rằng một mode ban đầu ở trạng thái chân không và mode kia
![]()
![]()
a b
ban đầu ở trạng thái Fock, cụ thể là trạng thái | 0 |1 . Lúc này nghiệm của hệ
mn
phương trình vi phân nói trên cho cij tcó dạng sau:
c01(t) c00(t),
00 01
1
![]()
![]()
![]()
3ia0t
i0t
i i0t
i
c 01 (t) e
4 e 2
cos x t sin x t e
2 cos x t sin x t ,
2
01
01
2
13ia0t
1
i0t
5 1
i
2
i0t
5
i
(3.9)
c10
(t) e
4 e 2
cos x1t sin x1t e
2 cos x2t sin x2t ,
![]()
2 5
![]()
c01(t) c00(t).
5
11 10
Các biên độ xác suất tìm được ở mục này sẽ được sử dụng để khảo sát sự sinh các trạng thái đan rối cực đại của hệ trong phần tiếp theo.
3.2.1.2. Ảnh hưởng của nhiễu trắng đối với sự tạo ra các trạng thái đan rối trong bộ nối tương tác tuyến tính được bơm một mode
Ở đây, chúng tôi sử dụng công thức entropy von Neumann (2.26) cho các biên độ xác suất ở (3.8) và (3.9) để khảo sát sự ảnh hưởng của nhiễu trắng đối
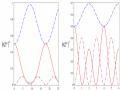
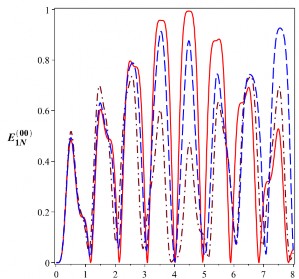
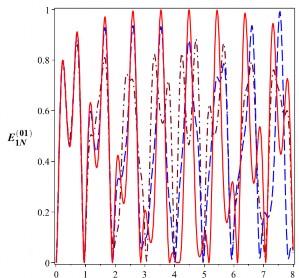
với sự tiến triển của entropy đan rối trong bộ nối phi tuyến tương tác tuyến tính được bơm một mode. Hình 3.1 mô tả sự tiến triển của entropy đan rối với các giá trị khác nhau của tham số a0.
t [10-6s] t [10-6s]
6
Hình 3.1: Sự tiến triển của các entropy đan rối
00
E
và
1N
01
E
1N
(đơn vị ebit) của các trạng
thái cắt với
0 10 rad/s. Đường nét liền ứng với
a0 0 , đường nét gạch ứng với
0
0
a 105rad/s và đường nét gạch chấm ứng với a 2105 rad/s
Khi
a0 0 , kết quả của
00
E
1N
trở nên giống với kết quả của Miranowicz và
1N
Leoński [20]. Entropy đan rối có thể đạt đến giới hạn 1 ebit hoặc gần với nó cho các trạng thái kiểu Bell được hình thành. Vì vậy, nó chứng minh rằng các bộ nối phi tuyến Kerr với các tương tác tuyến tính giữa các mode trường có thể được coi là nguồn của các trạng thái đan rối cực đại. Chúng ta có thể thấy rằng trong Hình
3.1, entropy đan rối
E01có thể đạt đến giới hạn 1 ebit hoặc gần với nó hơn so với
E
00
1N
và số lượng các đỉnh nhiều gấp đôi so với số đỉnh của
E00, tức là các dao
1N
động nhanh hơn hai lần. Đối với trường hợp a0 ≠ 0, chúng ta thấy rằng đối với
1N
E00, entropy đan rối tăng chậm trong khoảng 0 < t < 2x10-6s, giảm nhanh trong
khoảng 2x10-6s < t < 6x10-6s và tăng nhanh trong khoảng 6x10-6s < t < 8x10-6s so
1N
với trường hợp không có mặt của tham số a0. Đối với
E01, khi tham số a0 có mặt,
entropy đan rối hầu như giảm dần và các đỉnh có chiều cao thấp hơn sẽ biến mất dần, nhưng khi a0 tăng, các đỉnh lại tách thành hai đỉnh có chiều cao gần bằng nhau. Có thể kết luận rằng nếu có tham số liên quan đến thành phần nhiễu, giá trị
cực đại của entropy đan rối giảm so với trường hợp
a0 0
và các giá trị của
entropy đan rối gần như lớn hơn không, có nghĩa là các trạng thái của hệ hầu như là trạng thái đan rối. Kết quả là, tham số a0 liên quan đến thành phần nhiễu là một tham số quan trọng để điều khiển việc tạo ra các trạng thái đan rối cực đại.
![]()
![]()
![]()
![]()
Để khảo sát ảnh hưởng của nhiễu trắng đối với sự hình thành các trạng thái đan rối cực đại trong bộ nối phi tuyến tương tác tuyến tính được bơm một mode, chúng tôi sử dụng công thức (2.30) cho các biên độ xác suất tìm được ở (3.8) và
(3.9). Dễ dàng thấy rằng
b012 b002
và b012 b002 , vì vậy ta không cần phải vẽ các
![]()
![]()
![]()
![]()
11N
41N
21N
31N
B
đồ thị của xác suất để hệ tồn tại trong các trạng thái kiểu Bell
0111N
01
![]()
![]()
B
và
.
21N
![]()
![]()
Trong trường hợp các trạng thái ban đầu là trạng thái chân không hai
mode
| ![]() |
| ![]()
và trạng thái Fock n-photon
| ![]() |1
|1![]() , các xác suất để tạo ra các
, các xác suất để tạo ra các
a b
a b
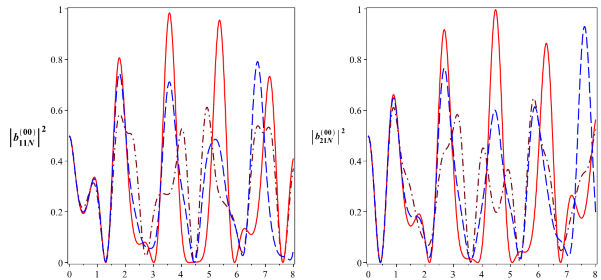
trạng thái kiểu Bell được mô tả trong các hình từ 3.2 đến 3.4.
t [10-6s] t [10-6s]
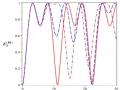
Hình 3.2: Xác suất để hệ tồn tại trong các trạng thái kiểu Bell
00
![]()
![]()
B
11N
00
![]()
![]()
B
5
và
21N
với
6
0 10 rad/s. Đường nét liền ứng với
a0 0 , đường nét gạch ứng với
a0 10 rad/s và
0
đường nét gạch chấm ứng với a 2 105rad/s
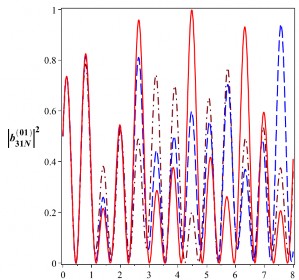
t [10-6s] t [10-6s]
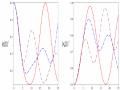
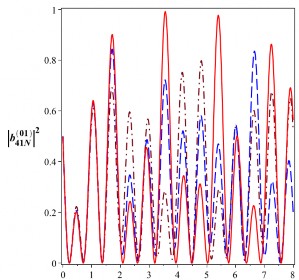
Hình 3.3: Xác suất để hệ tồn tại trong trạng thái Bell
01
![]()
![]()
B
31N
01
![]()
![]()
B
5
và
41N
với
106
0
rad/s. Đường nét liền ứng với
a0 0 , đường nét gạch ứng với
a0 10 rad/s và đường
0
nét gạch chấm ứng với a 2 105rad/s
t [10-6s] t [10-6s]
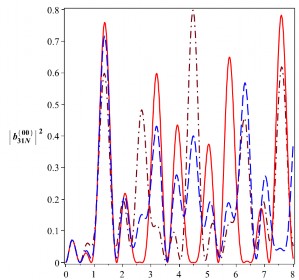
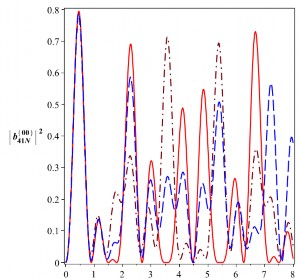
Hình 3.4: Xác suất để hệ tồn tại trong trạng thái Bell
00
![]()
![]()
B
31N
00
![]()
![]()
B
5
và
41N
với 0
106rad/s.
Đường nét liền ứng với
a0 0 , đường nét gạch ứng với
a0 10 rad/s và đường nét
0
gạch chấm ứng với a 2 105rad/s