Thứ Hạng Bách Phân (Percentile Ranks, Thường Viết Là Pr)

(2). Với đáp án trong câu TN, số người nhóm cao chọn phải nhiều hơn số người nhóm thấp.

(3). Với các mồi nhử, số người trong nhóm cao chọn phải ít hơn số người trong nhóm thấp.

Dựa và các tiêu chí trên chúng ta hoàn toàn có thể xây dựng được các đề trắc nghiệm chất lượng. Tuy nhiên như đã phân tích ở phần trước. Với các mẫu thay đổi, thì các tham số đặc trưng của câu hỏi (độ khó, độ phân biệt,..) cũng thay đổi theo. Nên trong lý thuyết CTT vẫn đề chọn mẫu là rất quan trọng.

1.2.2. Điểm số học tập

1.2.2.1. Điểm thô (raw scores)

Điểm số trên một bài thi (bài tự luận, bài trắc nghiệm lớp học hay bài trắc nghiệm được tiêu chuẩn hóa) thường được xác định bởi điểm của mỗi câu. Bài tự luận, điểm số một câu hỏi có thể lớn hơn 1, trong đó một số ý đặc trưng trong câu trả lời được cho điểm theo một thang điểm đã định trước. Với bài trắc nghiệm, mỗi câu hỏi chỉ có thể quy về đúng hay sai. Câu trả lời đúng thường được tính là 1 điểm. Tổng cộng các điểm số từng câu trắc nghiệm được gọi là điểm thô. Ta thấy điểm thô của bài trắc nghiệm không giúp ta so sánh giữa các bài trắc nghiệm có độ khó khác nhau. Vì vậy thường phải đổi điểm thô thành các loại điểm khác phù hợp với việc nghiên cứu, trình bày và giải thích. Hiện nay ở nước ta áp dụng điểm từ 0 đến 10.

1.2.2.2. Điểm phần trăm đúng

Có thể bạn quan tâm!

Xem toàn bộ 137 trang tài liệu này.

Điểm số này tính bằng tỉ lệ phần trăm, theo công thức: X = 100 Đ/T. Trong đó: X = điểm tính theo tỉ lệ %;

Đ = số câu học sinh làm đúng;

T = tổng số câu của bài trắc nghiệm.

Điểm phần trăm đúng so sánh điểm của học sinh này với điểm số tôi đa có thể đạt được. Đây là một loại điểm tuyệt đối. Yếu tố xác định điểm số này là độ khó của nội dung bài trắc nghiệm, cần thận trọng khi sử dụng nó, vì dễ bị chủ quan của người ra đề và thường không đo lường được mức khả năng thực của học sinh. Bởi vì người ra đề thi có thể thay đổi số câu trắc nghiệm dễ hay khó tùy theo ý muốn.

1.2.2.3. Điểm chữ

Về căn bản cũng giống như điểm phần trăm đúng, điểm chữ dùng các mẫu tự A, B, C, D, v.v… và có thể ấn định: điểm A gồm các điểm phần trăm đúng từ 90 đến 100, điểm B gồm các điểm phần trăm đúng từ 70 đến 89, điểm C gồm các điểm phần trăm đúng từ 50 đến 69, v.v….

1.2.2.4. Thứ hạng bách phân (Percentile Ranks, thường viết là PR)

Đây là điểm có được do sự biến đổi các điểm thô ra thành các trị số phần trăm trong một nhóm chọn làm chuẩn mực.

a) Định nghĩa: Thứ hạng bách phân là một con số nằm giữa 0 và 100, cho biết có bao nhiêu phần trăm trường hợp điểm số trong nhóm chuẩn mực rơi vào chính điểm số ấy hay ở dưới nó.

b) Ý nghĩa: Dùng điểm PR có thể so sánh điểm của các học sinh làm bài trắc nghiệm này với một nhóm lớn đã được chọn làm chuẩn mực.

1.2.2.5. Điểm tiêu chuẩn (Standard scores)

a) Mô tả: Điểm tiêu chuẩn là điểm biến đổi từ điểm thô dựa trên cơ sở độ lệch tiêu chuẩn của phân bố điểm số. Chúng có thể được xem như là những điểm số đã được gán cho một trung bình và một độ lệch tiêu chuân nào đó. Nó thường được sử dụng trong trắc nghiệm vì một số đặc tính sau:

- Mỗi loại điểm tiêu chuẩn có trung bình và độ lệch tiêu chuẩn chung cho mọi bài trắc nghiệm và mọi nhóm người.

- Điểm tiêu chuẩn cho phép ta thực hiện so sánh các trắc nghiệm hoặc giữa các nhóm người.

- Có thể xử lý bằng mọi phương pháp toán học.

b) Các loại điểm tiêu chuẩn thông dụng: điểm Z, điểm V. Ở nước ngoài còn có điểm Stanine (9 bậc), điểm C-Guilford, điểm T, Điểm AGCT, điểm CEEB. Về trắc nghiệm trí tuệ người ta dùng thương số trí tuệ IQ (với các trắc nghiệm Vechsler, Stanford - Binet, v.v…).

c) Ưu, nhược điểm của các loại điểm tiêu chuẩn: Điểm tiêu chuẩn có ưu điểm hơn điểm % đúng, thứ hạng bách phân vị nó có thể dùng tính toán hoặc đối chiếu các kết quả. Như: cộng các điểm tiêu chuẩn của nhiều bài trắc nghiệm môn học khác nhau để tính trung bình (ta vẫn hay làm trong điểm bài luận đề lâu nay); so sánh hai hay nhiều điểm trung bình của 1 bài trắc nghiệm ra trên nhiều nhóm, đối chiếu điểm trên các bài trắc nghiệm khác nhau; tính hệ số tương quan (với một bài trắc nghiệm đã chuẩn hóa)

để xác định tính giám của bài trắc nghiệm mới soạn. Nhược điểm của điểm tiêu chuẩn là:

+ Nếu các dữ kiện có độ xiên quá lớn thì việc sử dụng điểm tiêu chuẩn là không thích hợp vì là một loại điểm tương đối, nếu bài quá dễ hay quá khó đối với nhóm học sinh thì điểm trung bình bị lệch nhiều so với vùng trung tâm. Các điểm số không còn phản ánh đúng thực chất khả năng lĩnh hội bài học của học sinh.

+ Vì điểm tiêu chuẩn phụ thuộc vào độ lệch tiêu chuẩn nên khó giải thích ý nghĩa của các điểm số trắc nghiệm. Học sinh đạt 7 môn Anh văn có thể là giỏi trong lớp, trong khi điểm 7 môn Toán chỉ là khá trong lớp đó.

1.2.2.6. Công thức đổi điểm thô sang một số điểm tiêu chuẩn

a) . Điểm Z (Z score): Điểm Z liên hệ đến phân bố bình thường tiêu chuẩn với trung bình = 0 và độ lệch tiêu chuẩn = 1.

Công thức chuyển đổi: Z = (X – điểm trung bình X) / s

Trong đó X là một điểm thô; X = điểm thô trung bình của nhóm làm trắc nghiệm; s = độ lệch tiêu chuẩn của nhóm.

Điểm Z cho biết vị trí của một học sinh có điểm thô X so với trung bình của nhóm học sinh cùng làm bài trắc nghiệm..

Bảng Z và công dụng: Đây là bảng cho các trị số là diện tích tính theo tỉ lệ %. Diện tích này chính là tích phân (tích phân Laplace) giới hạn bởi đường cong bình thường tiêu chuẩn (đường Gauss, N(0,1)) với trục hoành tính từ giá trị Z = 0 (tức ngay tại trị trung bình) đến giá trị Z > 0 xác định nào đó (xin xem bảng Z đính kèm cuối chương này). Do tính đối xứng của đường cong qua trục tung (Z=0) nên tổng diện tích trong bảng (từ trung bình trở lên) sẽ là 50%.

Công dụng: trị số đọc trong bảng cho ta tính ước lượng tỉ lệ % học sinh ở phía dưới hay phía trên một học sinh đạt điểm số Z nào đó.

b) Điểm tiêu chuẩn V: Căn bản giống như điểm Z, nhưng được quy về phân bố bình thường có trung bình = 10 và độ lệch tiêu chuẩn là 4. Loại điểm này được áp dụng tại Việt Nam trước 1975, với hệ thống điểm cho từ 0 -> 20. Để có điểm V, trước hết đổi điểm thô X ra Z, sau đó áp dụng công thức và làm tròn số để nhận được giá trị nguyên:

Điểm tiêu chuẩn V = 4Z + 10 Ngày nay, để phù hợp với hệ thống điểm từ 0 -> 10, có thể dùng điểm tiêu chuẩn V mới với trung bình = 5 và độ lệch tiêu chuẩn là 2. Điểm V (mới) = 2Z + 5

Tổng quát, nếu ta đổi một điểm thô X sang một loại điểm tiêu chuẩn Xtc có trung bình = Mtc và độ lệch tiệu chuẩn = stc nhờ trung gian điểm Z thì áp dụng công thức: Điểm tiêu chuẩn Xtc = Stc Z + Mtc

Chúng ta đã làm quen với khái niệm điểm thô của bài trắc nghiệm cùng nhiều loại điểm số khác thường được sử dụng trong trắc nghiệm. Điểm thô là tổng điểm các câu học sinh làm đúng. Điểm phần trăm đúng, thứ bậc bách phân, điểm tiêu chuẩn là điểm được biến đổi từ điểm thô theo các cách khác nhau. Trong quá trình tiếp cận các công thức tính ta cũng tìm hiểu cả ý nghĩa và giải thích công dụng của từng loại điểm. Trong các loại điểm đã đề cập, ta chú ý nhiều đến điểm tiêu chuẩn vì các ưu điểm của nó. Tuy nhiên, ta cần nhớ rằng không có một loại điểm nào là hoàn hảo mà tùy thuộc vào mục đích sử dụng, vào tính chất của bài thi mà ta chọn một loại điểm phù hợp.

1.3. Lý thuyết ứng đáp câu hỏi

Lý thuyết đánh giá cổ điển (CTT) là cách tiếp cận chi phối cho đến năm 1953 khi Frederic Lord đã công bố luận văn tiến sĩ của mình về Lý thuyết năng lực tiềm ẩn (Latent Trait Theory). Vào những năm 1970, lý thuyết ứng đáp câu hỏi (IRT – Item Response Theory) bước đầu có những nghiên cứu một cách đột phá và đầy đủ. Đầu những năm 2000 khi các công cụ tính toán (phần mềm chuyên dụng) hỗ trợ tốt hơn ứng dụng IRT vào các hệ thống đánh giá, khảo thí mới thực sự diễn ra. Tuy nhiên các trung tâm nghiên cứu về IRT chủ yếu vẫn Mỹ hoặc liên quan đến các trường đại học ở Mỹ. IRT được xây dựng dựa trên một số tiên đề và dựa trên một hàm phân bố xác suất của năng lực thí sinh theo các tham số (độ khó,…) của câu hỏi.

1.3.1. Tổng quan về lý thuyết ứng đáp câu hỏi

Để đo lường năng lực của thí sinh (TS), chúng ta cần bộ câu hỏi (CH) được thiết kế đúng mục tiêu cần đo. Khi đó năng lực của thí sinh là một đại lượng ẩn, nó chỉ được biểu hiện thông qua quan sát phản ứng của TS với các câu hỏi. Chúng ta cần công nhận với nhau rằng:

- Năng lực tiềm ẩn (latent trait) cần đo chỉ có một chiều (unidimensionality), hoặc ta chỉ quan tâm đo một chiều của năng lực đó mà các chiều năng lực khác không ảnh hưởng .

- Các câu hỏi trong một bài thi là độc lập với nhau địa tức là việc trả lời một CH không ảnh hưởng đến các CH khác trong cùng một đề thi.

Khi đó chúng ta sẽ có một tương quan giữa năng lực của TS biểu hiện qua sự ứng đáp của TS vỡi mỗi câu hỏi và bộ công cụ đo (bộ CH) độc lập địa phương với nhau (các câu hỏi không ảnh hưởng lẫn nhau). Mô hình về mối tương quan này đã được Allen Birnbaum và Lord đề xuất mô hình vòm chuẩn (dạng phân phối chuẩn) để biểu diễn mỗi quan hệ năng lực ứng đáp của TS với CH. Tuy nhiên mô hình toán học của dạng vòm chuẩn là quá phức tạp, và Birnbaum còn đề xuất một mô hình có luôn tham số độ khó, độ phân biệt nên việc tính toán ban đầu gặp rất nhiều khó khăn. Năm 1960 (thực ra năm 1953) George Rasch đề xuất một mô hình mới là mô hình logistic thây thế cho mô hình vòm chuẩn, đồng thời Rasch chỉ đưa vào mô hình của mình một tham số là độ khó. Do vậy Rasch đã xây dựng được cơ sở lý thuyết của nó, phá dỡ các

rào cản mà mô hình của Lord và Birnbaum gặp phải. Thực tế sau này (những năm 70) các nhà nghiên cứu thế hệ hai đã dễ dàng chứng mình được hai mô hình: Vòm chuẩn và logistic là tương đương nhau đồng thời trên mô hình logistic ta có thể đưa vào các tham số khác ngoài độ khó như độ phân biệt, độ đoán mò,…. Chúng ta sẽ tiếp cận mô hình logistic lần lượt một, hai, ba tham số ở đoạn sau.

Ứng với mỗi câu hỏi trong đề thi, dùng đề đo các năng lực khác nhau, mỗi năng lực có các đáp ứng khác nhau lên câu hỏi. Theo [3, tr. 87] người ta giả định là có một hàm đặc trưng câu hỏi (Hàm ĐTCH - Item Characteristic Function) phản ánh mối quan hệ giữa các biến không quan sát được (năng lực của TS) và các biến quan sát được (việc trả lời CH). Đồ thị biểu diễn hàm đó được gọi là đường cong đặc trưng câu hỏi (Đường cong ĐTCH - Item Characteristic Curve).

Đối với các cặp TS – CH, cần xây dựng một thang đo chung để biểu diễn mối tương tác giữa năng lực tiềm ẩn và đáp ứng với độ khó câu hỏi. Theo [3, tr. 87 – 88], ta có thể biểu diễn năng lực tiềm ẩn của các TS bằng một biến liên tục θ dọc theo một trục, từ –∞ đến +∞. Khi xét phân bố năng lực của một tập hợp TS nào đó, ta gán giá trị trung bình của phân bố năng lực của tập hợp TS đó bằng không làm gốc của thang đo năng lực, và độ lệch tiêu chuẩn của phân bố năng lực bằng 1. Chọn một thuộc tính của CH để đối sánh với năng lực: tham số biểu diễn thuộc tính quan trọng nhất đó là độ khó b của CH (cần lưu ý là đại lượng độ khó ở đây sẽ được xác định khác với trong CTT). Cũng theo cách tương tự có thể biểu diễn độ khó của các CH bằng một biến liên tục dọc theo một trục, từ –∞ đến +∞. Khi xét phân bố độ khó của một tập hợp CH nào đó, ta chọn giá trị trung bình của phân bố độ khó đó bằng không (0), làm gốc của thang đo độ khó, và độ lệch tiêu chuẩn của phân bố độ khó CH bằng 1.

1.3.2. Hàm đặc trưng câu hỏi

Có nhiều cách tiếp cận để xây dựng mô hình hàm đặc trưng câu hỏi, nhưng cách xây dựng của Baker [10] là dễ hiểu và dễ tiếp cận. Tài liệu [3] của giáo sư Lâm Quang Thiệp viết về vấn đề này cũng hết sức logic, súc tích và dễ hiểu. Theo [3, tr. 89

– 91], Giả thiết cơ bản sau đây của George Rasch, nhà toán học Đan Mạch, được đưa ra làm cơ sở để xây dựng mô hình hàm đáp ứng CH một tham số:

Một người có năng lực cao hơn một người khác thì xác suất để người đó trả lời đúng một câu hỏi bất kì phải lớn hơn xác suất của người sau; cũng tương tự như vậy, một câu hỏi khó hơn một câu hỏi khác có nghĩa là xác suất để một người bất kì trả lời đúng câu hỏi đó phải bé hơn xác suất để trả lời đúng câu hỏi sau [16, tr. 117]

Với giả thiết nêu trên, theo [3, tr. 89 - 91] có thể thấy xác suất để một TS trả lời đúng một CH nào đó phụ thuộc vào tương quan giữa năng lực của TS và độ khó của CH. Chọn Θ để biểu diễn năng lực của TS, và β để biểu diễn độ khó của CH. Gọi P là xác suất trả lời đúng CH, xác suất đó sẽ phụ thuộc vào tương quan giữa Θ và β theo

một cách nào đó, do vậy ta có thể biểu diễn: f (P) 



(1)

Trong đó f là một hàm nào đó của xác suất trả lời đúng. Lấy logarit tự nhiên

của (1)ta được : ln f (P)  ln  ln  ln b



(2)

Khi xét mô hình trắc nghiệm nhị phân, Rasch chọn hàm f chính là mức được

thua (odds) O, hoặc khả năng thực hiện đúng (likelyhood ratio), tức là

f (P) 

1 P

biểu diễn tỉ số của khả năng trả lời đúng và khả năng trả lời sai nên ln

1 P

b

(3) Từ đó P

1 P

eb

hay

b

P() (4)

1 eb

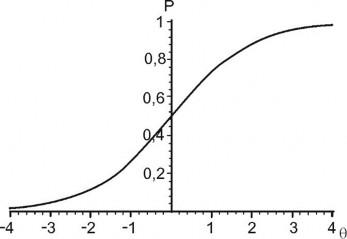
Hình 1.1 Đường cong ĐTCH một tham số