số hàm số logarit. Tính toám biểu thức logarit phức tạp. | ||||||
19 | Thông hiểu: Đạo hàm, tính chất của hàm số mũ, logarit, lũy thừa dạng hàm hợp. Tập xác định của hàm số hợp của hàm số lũy thữa, các bài toán ứng dụng đơn giản. | 32 | 24 | 4 | 21 | |
20 | Vận dụng: Phương trình , bất phương trình, hệ phương trình mũ chứa tham số, Phương trình, bất phương trình , hệ phương trình lôgarit chứa tham số, Cực trị hàm mũ, logarit. Nhận dạng đồ thị với các tính chất đạo hàm của hàm số. | 36 | 36 | 25 | 43 | |
21 | Vận dụng cao: Sử dụng công thức mũ,logarit, tính chất hàm số mũ, logarit trong các bài toán về tính chất , giá trị lớn nhất , nhỏ nhất của hàm số hợp của hàm số mũ, hàm số logarit, Phương trình mũ phức tạp, các ứng dụng thực tế | 47 | 49 | 44 | 47 | |
3. Nguyên hàm - tích phân và ứng dụng (7 câu) | 22 | Nhận biết: Khái niệm nguyên hàm, tích phân. Tìm họ nguyên hàm đơn giản | 7 | 2 | 18 | 8 |
23 | Nhận biết : Tính chất của nguyên hàm, tích phân và mối liên hệ giữa tích phân và nguyên hàm. Tìm họ nguyên hàm của hàm số dựa vào bảng nguyên hàm, tính chất nguyên hàm | 29 | 9 | 28 | 32 | |
24 | Thông hiểu : Tính tích phân của hàm số | 17 | 20 | 42 | 25 | |
25 | Thông hiểu : Ứng dụng tích phân trong bài toán diện tích, thể tích đơn giản | 40 | 40 | 38 | 19 | |
26 | Thông hiểu: Sử dụng tìm nguyên hàm, tích phân với các câu hỏi khác | 26 | 29 | 46 | 30 | |
27 | Vận dụng : Tính tích phân, kĩ thuật tính và ứng dụng | 49 | 42 | 10 | 46 | |
28 | Vận dụng cao: Sử dụng tìm nguyên hàm, tính tích phân của hàm số với các bài toán liên quan khác. Ứng dụng vào bài toán thực tế | 31 | 48 | 14 | 37 | |
4. Số phức | 29 | Nhận biết: Xác định các tham số cơ bản của số phức | 3 | 11 | 7 | 9 |
30 | Nhận biết: Các phép toán cơ bản với số phức, Các dạng biểu diễn của số phức | 11 | 6 | 2 | 4 |
Có thể bạn quan tâm!
-
Phân Tích Đa Chiều Năng Lực Của Ts Với Đề Thi 01. -
Biểu Đồ Tương Quan Giữa Năng Lực Của Thí Sinh Và Độ Khó Của Đề Thi 02 -
Mẫu Đặc Tả Kiến Thức Môn Toán 12 Theo Chuẩn Kiến Thức Kĩ Năng Bộ Giáo Dục Ban Hành. -
Triển khai đánh giá kết quả học tập môn Toán lớp 12 bằng một đề tổng hợp với các câu hỏi nhị phân, đa phân và đa chiều - 17
Xem toàn bộ 137 trang tài liệu này.
31 | Nhận biết: Nghiệm phương trình bậc nhất, bậc hai hệ số thực của số phức. | 22 | 15 | 19 | 15 | |
32 | Thông hiểu: Các bài toán tính toán liên quan đến dạng biểu diễn của số phức, nghiệm phức của phương trình. | 38 | 38 | 20 | 40 | |
33 | Thông hiểu: Các bài toán liên quan đến môđun, đến tính toán biểu thức phức | 42 | 25 | 40 | 29 | |
34 | Vận dụng: Các tính toán phức tạp, các bài toán hình học liên quan đến mô đun số phức. | 48 | 46 | 47 | 48 | |
5. Thể tích khối đa diện (5 câu) | 35 | Nhận biết: Thể tích khối chóp dễ xác định đường cao, diện tích đáy. Thể tích khối lăng trụ đứng dễ xác định đường cao, diện tích đáy | 24 | 30 | 11 | 23 |
36 | Thông hiểu: Tính thể tích khối chóp có liên quan đến yếu tố cạnh hoặc góc đơn giản . Tính thể tích khối lăng trụ đứng có liên quan đến yếu tố cạnh hoặc góc đơn giản | 41 | 41 | 22 | 29 | |
37 | Thông hiểu: Các khái niệm liên quan đến khối đa diện: Mặt, cạnh, đỉnh, mặt đối xứng,…, đa diện đều. Phân chia khối đa diện. | 13 | 23 | 43 | 14 | |
38 | Vận dụng: Tính thể tích khối chóp có sử dụng kiến thức ở mức độ cao hơn về quan hệ vuông góc, góc, khoảng cách để xác định đường cao, diện tích đáy. Tính thể tích khối lăng trụ có sử dụng kiến thức ở mức độ cao hơn về quan hệ vuông góc, góc, khoảng cách để xác định đường cao, diện tích đáy. Tính thể tích khối lăng trụ, khối hộp xiên. Kết hợp khối tròn xoay và khối đa diện. | 21 | 16 | 35 | 12 | |
39 | Vận dụng cao: Tính thể tích khối chóp không xác định trực tiếp phải sử dụng thông qua tỉ số thể tích, phân chia khối đa diện. Cực trị khối đa diện. | 44 | 44 | 48 | 45 | |
6. Khối tròn | 40 | Nhận biết: Công thức thể tích khối nón, diện tích xung quanh, diện tích toàn phần của hình nón. Công thức tính thể tích khối trụ, diện tích xung quanh ,diện tích toàn phần hình trụ. Diện tích mặt | 5 | 39 | 13 | 31 |
cầu và thể tích khối cầu. | ||||||
41 | Thông hiểu: Khối nón có liên quan thiết diện. Khối trụ có liên quan thiết diện | 39 | 22 | 45 | 35 | |
42 | Vận dụng: Xác định tâm và tính bán kính mặt cầu ngoại tiếp khối chóp. Nón, trụ có liên quan đến góc, khoảng cách, thiết diện. Thể tích khối trụ, diện tích xung quanh ,diện tích toàn phần hình trụ- Bài toán thực tế. | 45 | 45 | 24 | 50 | |
7. Phương pháp tọa độ trong không gian (8 câu) | 43 | Nhận biết: Các phép toán về véc tơ, điểm. | 10 | 10 | 5 | 11 |
44 | Nhận biết: Viết, xác định phương trình mặt phẳng khi biết một điểm và một vec tơ pháp tuyến | 20 | 1 | 21 | 10 | |
45 | Nhận biết: Viết, xác định phương trình đường thẳng khi biết một điểm và một vectơ chỉ phương | 2 | 17 | 3 | 24 | |
46 | Nhận biết: Viết phương trình mặt cầu khi biết tâm và bán kính. | 16 | 26 | 26 | 17 | |
47 | Thông hiểu: Các bài toán viết phương trình mặt phẳng, đường thẳng cần xác định được vectơ pháp tuyến hay chỉ phương liên quan điểm các đường thẳng, mặt phẳng đặc biệt.(hình chiếu, khoảng cách từ điểm lên các trục Ox, hay mặt phẳng (Oxy) | 28 | 19 | 16 | 28 | |
48 | Thông hiểu: Các bài toán liên quan đến tương giao, hình chiếu, khoảng cách của điểm, đường thẳng, mặt phẳng. | 33 | 33 | 33 | 34 | |
49 | Vận dụng: Các bài toán tìm điểm trên mặt phẳng, đường thẳng,… thỏa mãn các điều kiện cho trước. | 50 | 37 | 41 | 36 | |
50 | Vận dụng cao: Ứng dụng hình giải tích vào hình không gian hoặc xử lý các bài toán cực trị hình học liên quan đến véc tơ, điểm, mặt phẳng, mặt cầu, đường thẳng. | 37 | 50 | 49 | 49 |
Phụ lục 5: Đề thi thử nghiệm 01
KÌ THI KIỂM TRA KIẾN THỨC LỚP 12 Môn: Toán Thời gian làm bài: 90 phút |
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
|
Câu 2: Tìm tất cả các tiệm cận của đồ thị hàm số
y 2x 1.
x 1
A. x 1 và
y 2.
B. x 2 và
y 1.
C. x 1 và
y 2.
D. x 1 và
y 1.
Câu 3: Cho hàm số
y
3x. Mệnh đề nào dưới đây sai ?
A. Hàm số đã cho có tập xác định là D (0; ).
B. Hàm số đã cho đồng biến trên khoảng (; ).
C. Đồ thị của hàm số đã cho có tiệm cận ngang là trục Ox.
D. Đồ thị của hàm số đã cho đi qua điểm (0;1).
Câu 4: Trên mặt phẳng tọa độ, điểm
?
M (3;8) là điểm biểu diễn của số phức nào dưới đây
A. z 3 8i.
B. z 3 8i.
C. z 8 3i.
D. z 8 3i.
Câu 5: Hàm số
y x3 3x 4 đồng biến trên khoảng nào dưới đây ?
A. (1;1).
B. (1; ).
C. (; 1).
D. (; ).
Câu 6: Xét các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng ?
A. log(ab) log a.log b.
C. log(ab) log a log b.
B. log(ab) log a log b.
D. log(ab) a log b.
|
A. Cực đại của hàm số bằng -4. B. Cực đại của hàm số bằng -3.
C. Cực đại của hàm số bằng 1. D. Cực đại của hàm số bằng 0.
Câu 8: Tìm nguyên hàm của hàm số
6x
f (x) 6x.
A. f (x)dx ln 6 C.
C. f (x)dx 6x ln 6 C.
B. f (x)dx 6x C.
6
x1
D. f (x)dx C. x 1
Câu 9: Tìm phần thực a và phần ảo b của số phức z 1 2i 3i2.
A. a 4, b 2.
B. a 2, b 2.
C. a 2, b 2.
D. a 2, b 4.
Câu 10: Trong không gian với hệ tọa độ
Oxyz,
cho mặt phẳng (P) : 2x y 3z 2 0.
n
Vectơ nào dưới đây không phải là vectơ pháp tuyến của (P) ?
n
n
n
A. 4; 2; 6.
B. 2;1;3.
C. 2; 1;3.
D. 2; 1; 3.
Câu 11: Trong không gian với hệ tọa độ
(Oxz)?
Oxyz,
điểm nào dưới đây thuộc mặt phẳng
A. P 0; 2; 2.
B. Q 2;3; 4.
C. N 3; 1;0.
D. M 2;0;1.
Câu 12: Cho hình lập phương cạnh a . Gọi V1,V2
và V3
lần lượt là thể tích khối cầu ngoại
tiếp, thể tích khối cầu nội tiếp và thể tích khối cầu tiếp xúc với tất cả các cạnh của hình lập phương đã cho. Mệnh đề nào dưới đây đúng ?
V
2
A. 1 1.
2 3
V 2 V 2
2
V
B. 1 2.
2 3
V 2 V 2
C.11 .
V
2 3
2
V 2 V 22
2
V
D. 1 3.
2 3
V 2 V 2
Câu 13: Cho hàm số
f (x)
có đạo hàm
f (x) x2 (x 1). Hỏi hàm số
f (x)
đồng biến trên
khoảng nào dưới đây ?
A. (;0).
B. (;1).
C. (0;1). D. (1; ).
A I B D J C |
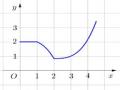
Câu 15: Tính môđun của số phức z, biết z (1 2i)2 (4 A. z 5 5. B. z 5. C. Câu 16: Cho hàm số y f (x) có đồ thị như hình bên. Tìm tất cả các giá trị của tham số thực m để phương trình f (x) 2m có nghiệm thuộc khoảng (1;1)? A. 0 m 4. B. 0 m 4. C. 0 m 2. D. 0 m 2. | 3i). z 25. D. |
z 15.
Câu 17: Trong không gian với hệ tọa độ
Oxyz,
cho hai điểm
I 1; 1; 0
và M (2;1;1).
Phương trình nào dưới đây là phương trình mặt cầu đi qua M và có tâm là I ?
A. (x 1)2 ( y 1)2 z2 10.
C. (x 1)2 ( y 1)2 z2 14.
B. (x 1)2 ( y 1)2 z2 14.
D. (x 1)2 ( y 1)2 z2 10.
2
Câu 18: Tính tổng S của tất cả các nghiệm của phương trình 52 x 7 x6 1.
A. S 3,5.
B. S 3.
C. S 3.
D. S 3,5.
Câu 19: Tính diện tích S của hình phẳng giới hạn bởi đồ thị
y e2 x ,
trục hoành, trục
tung và đường thẳng
x 2 ?
e4 1
A. S e4 e.
B. S . 2
C. S e4 1.
D. S 2e4 2.
Câu 20: Tìm tập xác định D của hàm số
y ln x 2 .
1x
A. D
{1}.
B. D (1; 2).
C. D (;1) (2; ).
1
D. D
{1, 2}.
Câu 21: Tính đạo hàm của hàm số
y e x .
1
1
1
1 1
1 11
A. y
.e x .
x2
B. y e x .
C. y
.e x .
x2
D. y
.e x .
x
Câu 22: Hàm số
y x2 (x 1)3 có bao nhiêu điểm cực tiểu ?
A. 1. B. 2. C. 3. D. 0.
Câu 23: Tính thể tích V của khối lăng trụ tam giác đều có cạnh đáy bằng 2a và chiều cao bằng 4a.
A. V 4 3a3.
B. V
3a3.
4 3a3
C. V . 3
3a3
D. V . 3
Câu 24: Trong không gian với hệ tọa độ
x 1t
Oxyz,
cho điểm
A1; 2;3
và đường thẳng
d : y 2t
z 3 t
. Phương trình đường thẳng đi qua A và song song với là:
A. x 1 y 2 z 3 . B. x 1 y 2 z 3 .
1 2 1 1 2 1
C. x 1 y 2 z 3 . D. x 1 y 2 z 3 .
1 2 1
8 x2
nếu
- 2 x 2
1 2 1
3
Câu 25: Cho hàm số
f (x) .
x2nếu x [2; 2]
Tính
I f (x)dx.
1
A. I 55 .
3
B. I 82 .
3
C. I 44 .
3
D. I 19 .
3
Câu 26: Cho biểu thức
x 8 1.x52 2 .x3
P
x 31 31
. Mệnh đề nào dưới đây đúng ?
A. P x1.
B. P x7 .
C. P x3.
D. P x5.
Câu 27: Tìm giá trị lớn nhất M của hàm số
y x
1x2 .
A. M 0.
B. M 1 .
2
C. M 1.
D. M 1 .
2
Câu 28: Trong không gian với hệ tọa độ Oxyz,
cho điểm
A2;3; 1. Gọi
M , N và P lần
lượt là hình chiếu vuông góc của A lên các trục mặt phẳng MNP.
x 'Ox, y 'Oy và
z 'Oz.
Viết phương trình
A. 3x 2y 6z 6 0.
C. 3x 2y 6z 6 0.
B. 3x 2y 6z 6 0.
D. 3x 2y 6z 6 0.
Câu 29: Cho các số thực x và y thỏa mãn
S x2 y2 2y.
(3x y)i x(2 i)2 6 13i.
Tính
A. S 1.
B. S 67.
C. S 7.
D. S 3.
Câu 30: Hàm số nào dưới đây không là nguyên hàm của hàm số
f (x) xex .
A. F(x) xex ex 7.
C. F(x) (x 1)ex 7.
B. F(x) xex ex 4.
D. F(x) (x 1)ex 2.
Câu 31: Trong không gian, cho hình chữ nhật ABCD có
AB 1, AC
5. Tính bán kính
R của hình trụ nhận được khi quay hình chữ nhật ABCD xung quanh trục AB ?
A. R 6.
b
B. R 2 6.
b
C. R 2.
D. R 4.
Câu 32: Biết
f (x)dx a 3b,
a
tính
I f (x) 2dx.
a
A. I 3a b.
B. I 3a 5b.
C. I a 3b 2.
D. I 5b a.
Câu 33: Tìm tất cả các giá trị của tham số thực m để đường thẳng
x y m 0
cắt đồ thị
hàm số hoành.
y 2x 1 tại hai điểm phân biệt
x 2
A, B sao cho trung điểm của đoạn AB thuộc trục
A. m 1 .
3
B. m 0.
C. m D. m 1 .
3
Câu 34: Trong không gian với hệ tọa độ
Oxyz, cho đường thẳng
d : x 3 y 2 z 1.
2 1 1
Viết phương trình đường thẳng d đối xứng với d qua mặt phẳng (P) : z 1 0.
A. d : x 1 y 3 z . B. d : x 1 y 3 z .
2 1 1 2 1 1
2 1 1 2 Câu 35: Hai hình chữ nhật có kích thước 28 được xếp chồng một phần lên nhau sao cho chúng đều nhận XY làm trục đối xứng tạo thành một hình phẳng như hình bên. Tính thể tích V của vật thể tròn xoay sinh bởi hình phẳng đã cho khi quay quanh XY. A. V 40. B. V 38. C. V 36. D. V 42. | 1 X | 1 Y |
C. d : x 3 y 2 z .
D. d: x 3 y 2 z 1.
Câu 36: Trong không gian với hệ tọa độ
Oxyz,
cho hai điểm
A1; 2; 4,
B(3;1; 1) và
đường thẳng
d : x y 1 z 3 . Điểm M thay đổi thuộc d ,
1 2 3
tính giá trị nhỏ nhất m của
tích vô hướng
A. m 1.
MA.MB ?
B. m 57 .
56
C. m 1 .
28
D. m 3 .
2
Câu 37: Một viên đá được bắn thẳng đứng lên trên với vận tốc ban đầu là 40 m/s từ một điểm cao 5 mét cách mặt đất. Vận tốc của viên đá sau t giây được cho bởi công thức v(t) 40 10t (m/s). Tính độ cao lớn nhất viên đá có thể lên tới so với mặt đất.
A. 80 m. B. 75 m. C. 90 m. D. 85 m.
Câu 38: Cho log 5 1, log 2.log 3 b. Tính P log 22log 32theo a và b.
30 a 5 5 5 5
A. P a2 2a 2b 1.
B. P a2 2b 1.
C. P a2 2b 1.
D. P a2 2a 2b 1.
Câu 39: Gọi
S1 , S2
lần lượt là diện tích toàn phần của hình lập phương
ABCD.ABCD
và diện tích toàn phần của tứ diện
ABCD. Tính k S2 .
S1
A. k 3 . 4
B. k 3 . 12
C. k 3 . 2
D. k 3 . 3
Câu 40: Cho a là số thực sao cho phương trình
z2 z a 0
có một nghiệm phức là
z 1 3 i. Kí hiệu z là nghiệm còn lại của phương trình đã cho và S z2 z2 . Mệnh
1 2 2 2 1 2
đề nào dưới đây đúng ?
A. S 3.
B. S 1 .
4
C. S 1.
D. S 3 .
4
3 4 x
Câu 41: Tập hợp tất cả các số thực x thỏa mãn 5
5 2x
3
là tập nào dưới đây ?
3
A. 2
B. 2
C. 2
D. 2
; .
5 ;+.
- 3;+ .
; .
5
Câu 42: Tìm tất cả các giá trị của tham số thực m để hàm số khoảng (;3).
y x 2
x m
nghịch biến trên
A. m 2.
B. 2 m 3.
C. m 3.
D. m 3.
|
|
