2.1. Néi dung kü thuËt
Chương 2
KỸ THUẬT CHIA ĐỂ TRỊ
Có thể nói rằng kĩ thuật quan trọng nhất, được áp dụng rộng rãi nhất để thiết kế các thuật toán có hiệu quả là kĩ thuật "chia để trị".
Nội dung của nó là: Ðể giải một bài toán kích thước n, ta chia bài toán đã cho thành một số bài toán con có kích thưóc nhỏ hơn. Giải các bài toán con này rồi tổng hợp kết quả lại để được lời giải của bài toán ban đầu. Ðối với các bài toán con, chúng ta lại sử dụng kĩ thuật chia để trị để có được các bài toán kích thước nhỏ hơn nữa. Quá trình trên sẽ dẫn đến những bài toán mà lời giải chúng là hiển nhiên hoặc dễ dàng thực hiện, ta gọi các bài toán này là bài toán cơ sở.
Tóm lại kĩ thuật chia để trị bao gồm hai quá trình: Phân tích bài toán đã cho thành các bài toán cơ sở và tổng hợp kết quả từ bài toán cơ sở để có lời giải của bài toán ban đầu. Tuy nhiên đối với một số bài toán, thì quá trình phân tích đã chứa đựng việc tổng hợp kết quả do đó nếu chúng ta đã giải xong các bài toán cơ sở thì bài toán ban đầu cũng đã được giải quyết. Ngược lại có những bài toán mà quá trình phân tích thì đơn giản nhưng việc tổng hợp kết quả lại rất khó khăn. Kĩ thuật này sẽ cho chúng ta một thuật toán đệ quy mà việc xác định độ phức tạp của nó sẽ phải giải một phương trình đệ quy như trong chương 1 đã trình bày.
Sơ đồ chia-để-trị gồm ba bước ở mỗi mức của đệ quy:
- Chia bài toán thành một số bài toán con.
- Trị các bài toán con bằng cách giải chúng đệ quy. Nếu kích thước các bài toán con là đủ nhỏ (bài toán cơ sở), giải trực tiếp các bài toán này.
- Kết hợp các lời giải của các bài toán con thành lời giải cho bài toán ban
đầu.
Phần tiếp sau trình bày một số ví dụ áp dụng kỹ thuật chia để trị để thiết kế
thuật toán cùng với sự đánh giá độ phức tạp tính toán của thuật toán.
2.2. C¸c vÝ dô ¸p dông
2.2.1. T×m min vµ max
1) Bài toán
Cho mảng a gồm n phần tử: a[1..n]. Tìm phần tử nhỏ nhất (min) và phần tử lớn nhất (max) trong dãy.
2) Thiết kế thuật toán
Tại mỗi bước chia đôi đoạn cần tìm rồi tìm min, max của từng đoạn, sau đó tổng hợp kết quả.
Nếu đoạn chỉ có một phần tử thì min = max và bằng phần tử đó. Hàm MinMax(a,l,r,Min,Max) cho Min và Max trong đoạn a[l..r].
Thuật toán
Input : a[1..n]
Output : Min = Min (a[1],..,a[n]),
Max = Max (a[1],..,a[n]).
MinMax(a,l, r, Min, Max) if (l == r)
{
}
Else
{
Min = a[l];
Max = a[l];
MinMax(a,l, (l+r)/ 2, Min1, Max1); MinMax(a,(l+r)/2 + 1, r , Min2, Max2); If (Min1 < Min2)
Min = Min1;
Else
Min = Min2;
If (Max1 > Max2) Max = Max1
Else
}
Max = Max2;
3) Đánh giá độ phức tạp tính toán của thuật toán
- Với n = 1, chỉ cần thực hiện 2 lệnh, do đó T(1) = O(1).
- Với n > 1 cần thực hiện lệnh các lệnh:
MinMax(a,l, (l+r) / 2, Min1, Max1);
MinMax(a,(l+r) /2 + 1, r , Min2, Max2); If (Min1 < Min2)
Else
Min = Min1;
Min = Min2;
If (Max1 > Max2) Max = Max1
Else
Max = Max2;
n
Ở đây có 2 lời gọi đệ quy với thời gian là T( 2 ). Khi kết thúc lời gọi đệ quy thì thực hiện phép so sánh và phép gán với thời gian là O(1). Tóm lại, ta có quan hệ sau:
T(1) = O(1)
n
T(n) = O(1) + 2T( 2 )
Thay các O(1) bởi các hằng nào đó, ta nhận được phương trình đệ quy:
C1 nếu n=1
Với n>1 ta có:
T(n)=
n
n
2T( 2 )+C2 nếu >1
T(n) = 2T( 2 ) + C2
n n
= 2(2T( 4 ) + C2) + C2 = 4T( 4 ) + 3C2
....
= 2iT(
n
2i ) + (2i - 1)C2
n
Quá trình dừng khi
2i =1
Khi đó:
n = 2i
i = log2n
T(n) = nT(1) +(2log2n -1)C2
= C1n + C2(2log2n -1)
Vậy T(n) = O(n)
2.2.2. Một số thuật toán sắp xếp Bài toán:
Cho dãy số a có n phần a1, a2, ..., an . Hãy sắp xếp dãy theo thứ tự tăng dần.
1) S¾p xÒp nhanh (Quicksort)
* Ý tưởng:
Chọn x là một phần tử làm biên (thường chọn là phần tử ở giữa dãy số). Phân hoạch dãy thành 3 dãy con
1. ak < x , với k = 1..i
2. ak = x , với k = i+1..j-1
3. ak > x , với k = j..n
ak=x | ak>x |
Có thể bạn quan tâm!
-
Ðộ Phức Tạp Của Chương Trình Có Gọi Chương Trình Con Không Đệ Qui -
Thiết kế và đánh giá thuật toán - 4 -
Thiết kế và đánh giá thuật toán - 5 -
Sắp Xếp Dãy A Theo Thứ Tự Tăng Dần Lúc Này A Đã Được Sắp Thứ Tự. -
Thiết kế và đánh giá thuật toán - 8 -
Trọng Lượng Và Giá Trị Của 4 Loại Đồ Vật Tính Đơn Giá Cho Các Loại Đồ Vật:
Xem toàn bộ 205 trang tài liệu này.
Hình 2.1. Phân hoạch dãy a thành 3 dãy con
Nếu số phần tử trong dãy con 1, dãy con 3 lớn hơn 1 thì ta tiếp tục phân hoạch theo phương pháp trên. Ngược lại thì dừng.
* Thiết kế thuật toán
Phân hoạch dãy am, am+1, ., an thành 2 dãy con:
Bước 1 : Chọn tùy ý một phần tử a[k] trong dãy là giá trị biên, m<= k <=n: x = a[k]; i = m; j = n;
Bước 2 : Phát hiện và hiệu chỉnh cặp phần tử a[i], a[j] nằm sai vị trí: Bước 2a : Trong khi (a[i]<x) i++;
Bước 2b : Trong khi (a[j]>x) j--; Bước 2c : Nếu i<= j
// a[i]>= x; a[j]<=x mà a[j] đứng sau a[i] Hoán vị (a[i],a[j]);
i++; j--;
Bước 3 :
Nếu i < j: Lặp lại Bước 2.//chưa xét hết mảng Ngược lại: Dừng
Có thể phát biểu thuật toán một cách đệ qui như sau : Bước 1 : Phân hoạch dãy am … an thành các dãy con :
- Dãy con 1 : am.. aj < x
- Dãy con 2 : aj+1.. ai-1 = x
- Dãy con 3 : ai.. an > x
Bước 2 :
Nếu ( m < j ) // dãy con 1 có nhiều hơn 1 phần tử Phân hoạch dãy am.. aj
Nếu ( i < n ) // dãy con 3 có nhiều hơn 1 phần tử
Phân hoạch dãy ai.. an Chẳng hạn cho dãy số a:
12 2 8 5 1 6 4 15
Phân hoạch đoạn l=1, r = 8: x = A[4] =5
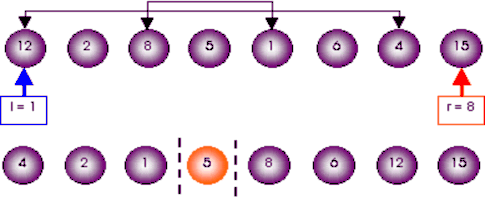
Phân hoạch đoạn l =1, r = 3: x = A[2] = 2
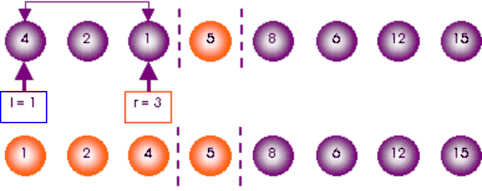
Phân hoạch đoạn l = 5, r = 8: x = A[6] = 6
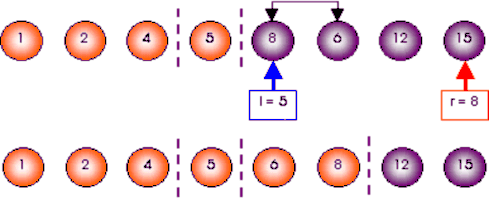
Phân hoạch đoạn l = 7, r = 8: x = A[7] = 6
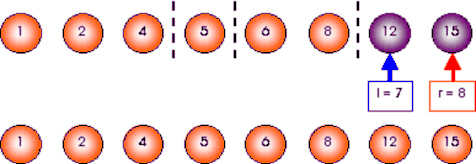
Hình 2.2. Sắp xếp dãy a theo thứ tự tăng dần
Quich-Sort(a,l,r)
{
i = l; j = r;
x = a[(l+r)/2]; // Chọn phần tử giữa while (i <= j)
{
while (a[i] < x ) i++;
while (a[j] > x)
j--;
if (i <= j)
{
tg = a[i];
a[i]=a[j]
a[j]=tg; i++;
}
if (l < j)
j--
}
QS(a,l,j); if (r > i )
QS(a,i,r);
* Đánh giá độ phức tạp tính toán của thuật toán
Gọi T(n) là thời gian thực hiện thuật toán, p(n) là thời gian để phân một dãy n phần tử thành hai dãy con thì:
T(n) = p(n) + T(J-l) + T(r-i)
= Cn + T(J-l) + T(r-i) (C là hằng số)
Trường hợp xấu nhất xảy ra khi phần tử được chọn luôn là lớn nhất hoặc nhỏ nhất: sau khi phân hoạch một trong hai dãy con chỉ có một phần tử, dãy kia gồm n-1 phần tử (khi j = l hoặc r = i)
Giả sử j = l thì ta có:
T(n) = Cn + T(0) + T(n-1)
= Cn + T(n-1)
= Cn + C(n-1) + T(n-2)
....
= Cn + C(n-1)+ ... +C + T(0)
= C n( n 1 )
2
Vậy T(n) = O(n2)
Trường hợp tốt nhất xảy ra khi dãy luôn được chia đôi. Khi đó ta có phương trình truy hồi:
T(n)=
n
C nếu n=1
2T( n ) + n nếu n>1
2
Trong đó: 2T( 2 ) là thời gian sắp xếp hai dãy con n là thời gian kiểm tra mỗi phần tử
Ta có với n>1 thì:
n
T(n) = 2T( 2 ) + n
n n n
= 2(2T( 4 )+ 2 ) + n = 4T( 4 ) +2 n
n n n
= 4(2T( 8 )+ 4 ) + 2n = 8T( 8 ) +3n
Dừng khi
= 2iT(
n =1
2i
n ) +i.n
2i
n= 2i
i= log2n Và khi đó ta có:
T(n) = nT(1) + nlog2n
= Cn + nlog2n
= O(nlog2n)
Trường hợp trung bình người ta đã chứng minh được rằng: T(n)= O(nlog2n)
2) Sắp xếp trộn
* Ý tưởng
Thuật toán sắp xếp kiểu trộn hai đường trực tiếp được thực hiện theo nhiều bước lặp. Mỗi bước lặp bao gồm hai giai đoạn :
Giai đoạn 1:
Phân bố luân phiên từng p phần tử từ dãy a vào các dãy trung gian b và c trong khi chưa hết dãy a.
Giai đoạn 2:
Trộn từng bộ p phần tử trong dãy b với p phần tử trong c, kết quả trộn được đưa vào a, trong khi chưa hết dãy b và chưa hết dãy c.
Các bước lặp còn được thực hiện trong khi p còn ≤ n . Bước đầu tiên p được khởi động bằng 1.