Sắp Xếp Dãy A Theo Thứ Tự Tăng Dần Lúc Này A Đã Được Sắp Thứ Tự.

Mỗi bước lặp sau( sau một lần phân bố và trộn ), số phần tử p sẽ khởi động lại là : p = p * 2 .

Ví dụ 2.1.

Giả sử a là dãy sau:

11

34

20

8

65

25

11

45

21

70

15

20

8

Có thể bạn quan tâm!

• Thiết kế và đánh giá thuật toán - 4
• Thiết kế và đánh giá thuật toán - 5
• Một Số Thuật Toán Sắp Xếp Bài Toán :
• Thiết kế và đánh giá thuật toán - 8
• Trọng Lượng Và Giá Trị Của 4 Loại Đồ Vật Tính Đơn Giá Cho Các Loại Đồ Vật:
• Thiết kế và đánh giá thuật toán - 10

Xem toàn bộ 205 trang tài liệu này.

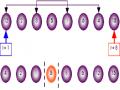
Đầu tiên ta phân bố luân phiên từng phần tử của dãy a vào các dãy trung gian b và c (p=1).

11

20

65

11

21

15

8

+ Lần phân bố đầu tiên (p=1) Dãy b:

Dãy c:

34

8

25

45

70

20

Thực hiện trộn hai đường từng phần tử của b với từng phần tử của c, kết quả đưa vào dãy a.

11, 34

8, 20

25, 65

11, 45

21, 70

15, 20

8

11, 34

25, 65

21, 70

8

+ Lần phân bố thứ 2 (p=2) Dãy b:

Dãy c:

8, 20

11, 45

15, 20

Thực hiện trộn hai đường p phần tử của b với p phần tử của c, kết quả đưa vào dãy a.

8, 11, 20, 34

11, 25, 45, 65

15, 20, 21, 70

8

8, 11, 20, 34

15, 20, 21, 70

+ Lần phân bố thứ 3 (p=4) Dãy b:

Dãy c:

11, 25, 45, 65

8

8, 15, 20, 21, 70

Thực hiện trộn hai đường p phần tử của b với p phần tử của c, kết quả đưa vào dãy a.

8, 11, 11, 20, 25, 34, 45, 65

8, 11, 11, 20, 25, 34, 45, 65

+ Lần phân bố thứ 4 (p=8) Dãy b:

Dãy c:

8, 15, 20, 21, 70

Thực hiện trộn hai đường p phần tử của b với p phần tử của c, kết quả đưa vào dãy a.

8, 8, 11, 11, 15, 20, 20, 21, 25, 34, 45, 65, 70

Hình 2.3. Sắp xếp dãy a theo thứ tự tăng dần Lúc này a đã được sắp thứ tự.

* Thiết kế thuật toán

input a[1..n]; // dãy cần sắp Output a đã được sắp

Mô tả: p = 1;

Trong khi (p <= n) ta thực hiện :

{

- Trong khi chưa hết dãy a thì phân bố luân phiên từng p phần tử từ dãy a vào các dãy trung gian b và c

- Trong khi chưa hết dãy b và chưa hết dãy c thì trộn từng cặp p phần tử trong dãy b với p phần tử trong dãy c, kết quả ghi vào a.

- p = 2p

}

Mô tả trên có thể viết thành hàm : mergesort()

{

p = 1;

while ( p <= n )

{

distribution (p); merge(p);

p = p * 2;

}

}

Như vậy, thuật toán chủ yếu được xây dựng trên 2 công việc :

- distribution(p) : Phân bố luân phiên p phần tử từ dãy a vào các dãy trung gian b, c trong khi chưa hết dãy a.

- merge(p) : Trộn từng cặp p phần tử trong b, và p phần tử trong c, kết quả lưu trử vào a, trong khi chưa hết dãy b và chưa hết dãy c.

Với công việc thứ nhất:

Phân bố luân phiên p phần tử từ dãy a vào các dãy trung gian b, c cho đến hết

dãy a.

Input a;

Output b, c; Mô tả

Thực hiện

{

Đọc từng p phần tử trong a và chép luân phiên vào b, c;

}

Trong khi (chưa hết dãy a);

Trong mô tả trên, có 2 thao tác con cần phải lưu ý : Thao tác 1:

Làm thế nào để xử lý một cách tự động việc chép luân phiên vào b và c. Ta thực hiện bằng cách : Dùng một khoá k, với k  {1,2} và quy định :

Nếu k = 1 thì chép vào b; Nếu k = 2 thì chép vào c;

Giả sử đầu tiên cho k = 1 để quyết định chép p phần tử của a vào b trước.

Sau mỗi lần chép xong p phần tử, ta chỉ cần khởi động lại giá trị k = 3-k .

Thao tác 2:

Đọc p phần tử của a chép vào b như thế nào ? Ta đọc từng phần tử của a và chép phần tử đó vào b; Việc đọc chép từng phần tử này còn được thực hiện trong khi chưa đủ p phần tử và chưa hết dãy a.

Vậy thao tác phân bố có thể mô tả chi tiết như sau :

do

{

i = 1;

while ( (i <= p) && (chưa hết dãy a) )

{

Đọc phần tử thứ i trong a; if ( k == 1)

chép vào b;

else

i++;

}

chép vào c;

k = 3-k;

}

while(chưa hết dãy F);

Thao tác phân bố cài đặt thành một hàm như sau :

//F, F1, F2, n, h1,h2 là các biến toàn cục. distribute(p)

{

int i, k=1, l = 1; h1 = 0; h2 = 0;

do

{

i = 1;

while( i<=p && l <= n)

{

if(k==1)

{

}

k = 3-k;

}

}

else

{

} i++; l++;

h1++;

F1[h1] = F[l];

h2++;

F2[h2] = F[l];

while(l <= n);

}

Với công việc thứ hai:

Trộn từng bộ p phần tử trong c, và p phần tử trong c, kết quả lưu tr? vào a, trong khi chưa hết b và c.

Input b, c;

Output a;

Mô tả :

Trong khi ( chưa hết dãy b và chưa hết dãy c )

{

Trộn từng cặp p phần tử của b và của c vào a;

}

Trong khi (chưa hết dãy c)

chép các phần tử còn lại của c vào a; Trong khi (chưa hết dãy b)

chép các phần tử còn lại của b vào a;

Ta cần chỉ rò công việc trộn từng cặp p phần tử của b và của c vào a hoạt động như thế nào ? Đó là :

- (*) : Đọc từng phần tử trong b, trong c, so sánh giá trị của chúng, giá trị nào nhỏ hơn thì chép phần tử tương ứng vào a. Nếu là phần tử của b thì đọc tiếp 1 phần tử của b; ngược lại thì đọc tiếp 1 phần tử của c

- ( ** ) :Thao tác trên còn được thực hiện trong khi : chưa đọc đủ p phần tử trong b và chưa đọc đủ p phần tử trong c và chưa hết dãy c và chưa hết dãy b;

Vòng lặp (**) dừng khi đã đọc đủ p phần tử trong c, hoặc đã đọc đủ p phần tử trong b, hoặc hết dãy b hoặc hết dãy c; Và khi đó ta cần xử lý các trường hợp sau :

Trong trường hợp chưa hết dãy b và chưa hết dãy c :

Nếu chưa đủ p phần tử trong b, thì đọc và chép các phần tử của b vào a cho đủ p. Tương tự như vậy cho c.

* Đánh giá độ phức tạp tính toán của thuật toán

Ta nhận xét rằng, trong phương pháp sắp xếp bằng trộn hai đường trực tiếp, số lượng các bước sao chép các phần tử từ dãy này sang dãy kia còn lớn hơn số lượng các bước so sánh giữa các phần tử : Vì ứng vớùi một lần so sánh thì có một thao tác sao chép, nhưng nếu một dãy nào đó xử lý cạn (hết dãy) thì phần đuôi của dãy còn lại được sao chép mà không ứng với một phép so sánh nào. Vì thế, đối với phương pháp này, ta chọn phép sao chép làm căn cứ đánh giá thời gian thực hiện của thuật toán.

Trong mỗi lần phân bố và trộn thì toàn bộ n phần tử được duyệt qua, so sánh và chép vào dãy đích (output). Như vậy thời gian chi phí cho mỗi bước có cấp là O(n).

Vì trong mỗi bước (bước thứ k) ta giải quyết được 2k = p giá trị và tiến trình dừng khi p ≥ n nên ta có lg2n bước, do đó cấp thời gian chi phí cho phương pháp này là O(nlg2n).

Một nhượïc điểm của phương pháp sắp xếp bằng kiểu trộn hai đường trực tiếp là chi phí cho không gian quá lớn: nó đòi hỏi cung cấp vùng nhớ 2n phần tử, gấp đôi so với phương pháp thông thường. Do đó phương pháp này chỉ thích hợp khi ta thao tác trên các tệp.

Mặt khác, phương pháp sắp xếp kiểu trộn hai đường trực tiếp có một nhược diểm quan trọng nữa là nó tự giới hạn số lượng các giá trị cố định là 1, 2, 4,.., 2k, trong đó 2k < n. Như vậy ta luôn luôn phải duyệt qua k bước chia và trộn. Nếu cho phép số lượng các phần tử trong một lần trộn có kích thước khác thì số các bước có thể giảm đi và trong trường hợp này việc sắp xếp có khả năng kết thúc sớm.

2.2.3. T×m kiÒm nhÞ ph©n

1) Bài toán

Cho dãy a gồm n phần tử đã được sắp tăng dần và một phần tử x. Tìm x có trong a hay không? Nếu có x trong a thì cho kết quả là chỉ số của phần tử đó, ngược lại cho kết quả 0.

2) Ý tưởng

Chia đôi dãy, mỗi lần chia đôi so sánh phần tử giữa x với nếu x bằng phần tử giữa thì dừng, ngược lại nếu x nhỏ hơn phần tử giữa thì lấy nửa trái, ngược lại thì lấy nửa phải

3) Thiết kế thuật toán

+ l là chỉ số dưới của dãy a

+ r là chỉ số dưới của dãy a

+ m là chỉ số giữa. Mô tả thuật toán:

- Nếu l > r kết thúc và trả lại giá trị 0 (không tìm thấy)

- Nếu l<=r thì:

+ tính m=[(l+r)/2];

+ So sánh x và a[m]:

Nếu x= a[m]: kết thúc và trả lại m ngược lại

nếu x<a[m]: tìm kiếm (đệ quy) ở nửa trái- từ a[l] đến a[m-1] ngược lại tìm kiếm (đệ quy) ở nửa phải- từ a[m+1] đến a[r]

Thuật toán:

KNP(l,r,a,x)

{

if(l>r) loc=0;

else

{

m=[(l+r)/2];

if(x<a[m]) loc=TKNP(l,m-1,a,x); else

if(x>a[m]) loc=TKNP(m+1,r,a,x) else

loc=m;

return(loc);

}

4) Đánh giá độ phức tạp tính toán của thuật toán

- Xây dựng phương trình truy hồi:

c1 nếu n=1

T(n)=

Với n>1 ta có:

T( n )+c2 nếu n>1

2

n

T(n) = T( )+ c2

2

= T( n )+ 2c2

4

= T( n )+ 3c2

8

....

= T(

n )+ ic2

2i

Dừng khi

n =1

2i

 n=2i

 i=log2n

Do đó T(n) = T(1) + c2log2n

= c1 + c2log2n