Sức bền vật liệu - 1

LỜI NÓI ĐẦU

Sức bền vật liệu là một phần kiến thức căn bản đối với kỹ sư thuộc các ngành kỹ thuật, vì vậy môn học này được bố trí trong chương trình đào tạo của nhiều trường đại học như Đại học Bách khoa Hà Nội, Đại học Giao thông vận tải, Đại học Thuỷ lợi, Đại học Xây dựng,… Ở trường Đại học Sư phạm Kỹ thuật Nam Định, môn học này được giảng dạy cho sinh viên hệ đại học chuyên nghành Cơ khí. Hiện nay, các trường đại học đều có tài liệu riêng giảng dạy về môn học này với nội dung, thời lượng và khối lượng kiến thức rất khác nhau do đặc thù của ngành.

Chính vì vậy việc biên soạn một bài giảng môn học Sức bền vật liệu riêng cho sinh viên trường Đại học Sư phạm Kỹ thuật Nam Định là rất cần thiết. Theo chương trình môn học Sức bền vật liệu được xây dựng để giảng dạy cho sinh viên ngành Cơ khí được xây dựng kế tiếp các nội dung cơ bản của Sức bền vật liệu đã được viết trong tập bài giảng Cơ học 1 giảng dạy cho sinh viên ngành Cơ khí trường Đại học Sư phạm Kỹ thuật Nam Định, nội dung của môn học bao gồm 4 chương với các nội dung chính: Thanh chịu tải trọng phức tạp, hệ thanh siêu tĩnh, ổn định hệ thanh và tải trọng động.

Cuốn bài giảng được viết trên cơ sở chương trình môn học Sức bền vật liệu. Người biên soạn đã cố gắng trình bày những vấn đề cơ bản của Cơ học vật rắn biến dạng theo quan điểm hiện đại, đảm bảo tính sư phạm và yêu cầu chất lượng của một bài giảng giảng dạy đại học. Những kiến thức trình bày trong bài giảng này là những kiến thức tối thiểu, cần thiết để sinh viên có thể học các môn học tiếp theo của các ngành Công nghệ hàn, công nghệ Ô tô, công nghệ chế tạo máy…

Cuốn bài giảng được biên soạn lần đầu nên chắc chắn còn nhiều thiếu sót. Chúng tôi rất mong nhận được sư góp ý của các đồng nghiệp và các em sinh viên để có điều kiện sửa chữa, hoàn thiện hơn cuốn bài giảng nhằm phục vụ tốt hơn cho công tác giảng dạy và học tập. Các ý kiến đóng góp xin gửi về địa chỉ: Bộ môn Kỹ thuật cơ sở, Khoa cơ khí, Trường Đại học Sư phạm Kỹ thuật Nam Định.

Nhóm tác giả biên soạn

MỤC LỤC

LỜI NÓI ĐẦU i

MỤC LỤC ii

Có thể bạn quan tâm!

• Sức bền vật liệu - 2
• Thanh Mặt Cắt Ngang Tròn Chịu Uốn Đồng Thời Xoắn
• Trục Chịu Uốn Và Xoắn Đồng Thời Các Biểu Đồ Nội Lực Được Biểu Diễn Trên Các Hình 1.22B, C, D. Thay Số Vào Ta Được:

Xem toàn bộ 91 trang tài liệu này.

Chương 1 1

THANH CHỊU LỰC PHỨC TẠP 1

1.1. KHÁI NIỆM CHUNG 1

1.1.1. Thanh chịu lực đơn giản 1

1.1.2. Thanh chịu lực phức tạp 1

1.1.3. Ứng suất trên tiết diện 1

1.2. THANH CHỊU UỐN XIÊN 2

1.2.1. Khái niệm 2

1.2.2. Ứng suất pháp trên mặt cắt ngang 3

1.2.3. Vị trí đường trung hoà 3

1.2.4. Biểu đồ ứng suất pháp trên mặt cắt ngang 4

1.2.5. Điều kiện bền 4

1.3. THANH CHỊU UỐN ĐỒNG THỜI KÉO (NÉN) 8

1.3.1. Khái niệm 8

1.3.2. Ứng suất pháp trên mặt cắt ngang 8

1.3.3. Vị trí đường trung hoà 9

1.3.4. Biểu đồ ứng suất pháp trên MCN 9

1.3.5. Điều kiện bền 10

1.3.6. Khái niệm về lòi mặt cắt ngang 10

1.4. THANH CHỊU KÉO (NÉN) LỆCH TÂM 13

1.4.1. Biểu thức ứng suất trên tiết diện 13

1.4.2. Đường trung hoà khi kéo (nén) lệch tâm 15

1.5. THANH CHỊU UỐN VÀ XOẮN ĐỒNG THỜI 17

1.5.1. Thanh có mặt cắt tròn 18

1.5.2. Thanh có mặt cắt hình chữ nhật 19

CÂU HỎI ÔN TẬP CHƯƠNG 1 25

Chương 2 27

GIẢI HỆ SIÊU TĨNH BẰNG PHƯƠNG PHÁP LỰC 28

2.1. KHÁI NIỆM CHUNG 28

2.2 NỘI DUNG PHƯƠNG PHÁP LỰC 29

2.2.1 Hệ cơ bản của hệ siêu tĩnh 29

2.2.2. Hệ tĩnh định tương đương 29

2.2.3. Tính hệ siêu tĩnh đối xứng 30

2.3. DẦM LIÊN TỤC 33

2.3.1. Định nghĩa 33

2.3.2. Phương trình ba mômen 33

2.3.3. Trường hợp đặc biệt 35

2.4. PHÉP NHÂN BIỂU ĐỒ VÊRÊXAGHIN 37

2.5. CÁCH TÍNH CHUYỂN VỊ TRONG HỆ SIÊU TĨNH 42

CÂU HỎI ÔN TẬP CHƯƠNG 2 43

Chương 3 44

ỔN ĐỊNH CỦA THANH THẲNG CHỊU NÉN, UỐN 44

3.1. KHÁI NIỆM CHUNG 44

3.2. BÀI TOÁN EULER XÁC ĐỊNH LỰC TỚI HẠN 46

3.2.1. Thanh thẳng liên kết khớp ở hai đầu 46

3.2.2. Thanh thẳng có liên kết khác ở hai đầu 48

3.3. ỨNG SUẤT TỚI HẠN. GIỚI HẠN ÁP DỤNG CÔNG THỨC EULER 49

3.3.1. Ứng suất tới hạn, độ mảnh 49

3.3.2. Giới hạn áp dụng công thức Euler 50

3.4 ỔN ĐỊNH CỦA THANH LÀM VIỆC NGOÀI GIỚI HẠN ĐÀN HỒI 50

3.5. PHƯƠNG PHÁP THỰC HÀNH TÍNH ỔN ĐỊNH 51

3.6. THANH CHỊU UỐN NGANG VÀ UỐN DỌC ĐỒNG THỜI 53

3.6.1. Khái niệm, phương trình vi phân của đường đàn hồi 53

3.6.2. Biểu thức gần đúng của độ vòng 55

3.6.3. Biểu thức gần đúng của mô men uốn 56

3.6.4. Ứng suất và điều kiện bền. 57

3.7. THANH CÓ ĐỘ MẢNH LỚN CHỊU NÉN LỆCH TÂM 57

3.8. ỔN ĐỊNH CỦA DẦM CHỊU UỐN 59

3.9. CÁC VÍ DỤ 61

3.10. CHỌN HÌNH DẠNG HỢP LÝ CỦA MẶT CẮT VÀ VẬT LIỆU 64

CÂU HỎI ÔN TẬP CHƯƠNG 3 65

Chương 4 67

TẢI TRỌNG ĐỘNG 67

4.1. KHÁI NIỆM CHUNG 67

4.1.1. Tải trọng tĩnh, tải trọng động 67

4.1.2. Phân loại tải trọng động 67

4.1.3. Các giả thiết khi tính toán 67

4.2. BÀI TOÁN CÓ GIA TỐC KHÔNG ĐỔI 68

4.2.1. Bài toán kéo vật nặng lên cao nhanh dần đều 68

4.2.2. Bài toán chuyển động quay với vận tốc góc không đổi 69

4.3. BÀI TOÁN CÓ GIA TỐC THAY ĐỔI THEO THỜI GIAN 72

4.3.1. Bậc tự do của hệ 72

4.3.2. Phương trình vi phân tổng quát của hệ một bậc tự do 72

4.4. BÀI TOÁN DAO ĐỘNG TỰ DO 73

4.4.1. Khái niệm chung về dao động 73

4.4.2. Dao động của hệ đàn hồi một bậc tự do 74

4.5. BÀI TOÁN VA CHẠM 77

4.5.1. Va chạm theo phương thẳng đứng 77

4.5.2. Va chạm theo phương nằm ngang 80

4.5.3. Kết luận chung về bài toán va chạm 82

CÂU HỎI ÔN TẬP CHƯƠNG 4 84

TÀI LIỆU THAM KHẢO 86

Chương 1

THANH CHỊU LỰC PHỨC TẠP

1.1. KHÁI NIỆM CHUNG

1.1.1. Thanh chịu lực đơn giản

Những trường hợp chịu lực của thanh khi kéo (nén), uốn phẳng, xoắn đã xét trong học phần Cơ học 1 được gọi là những trường hợp chịu lực đơn giản. Lúc này, trên tiết diện của thanh chỉ tồn tại một loại ứng lực độc lập: hoặc lực dọc, hoặc mô men uốn đi kèm theo lực cắt, hoặc mô men xoắn.

1.1.2. Thanh chịu lực phức tạp

Tổ hợp những trường hợp chịu lực đơn giản được gọi là trường hợp chịu lực phức tạp.

Tổng quát nhất trên tiết diện của thanh có đủ sáu thành phần ứng lực như hình vẽ 1.1 bao gồm:

- Lực dọc: Nz

- Mô men uốn: Mx , My

- Lực cắt: Qx, Qy

- Mô men xoắn: Mz

Hình 1.1: Thanh chịu lực phức tạp tổng quát

1.1.3. Ứng suất trên tiết diện

Theo nguyên lý cộng tác dụng thì ứng suất và biến dạng của thanh khi chịu lực phức tạp sẽ bằng tổng ứng suất hoặc tổng biến dạng do từng lực gây ra riêng rẽ.

Ứng suất pháp trên tiết diện chỉ do lực dọc, mô men uốn gây ra và bằng:

x y

rrN rM rM 

Các ứng suất thành phần có cùng phương nên ta viết tổng theo trị số đại số:

N M x M y 

N M x

A Ix

y M y x I y

(1.1)

Ứng suất tiếp trên tiết diện chỉ do lực cắt, mô men xoắn gây ra và bằng:

y x z

r r Q r Q r M 

(1.2)

Các ứng suất tiếp thành phần có phương khác nhau nên không chuyển được biểu thức sang phép cộng đại số.

y

Thành phần r Q có phương chiều phù hợp với lực cắt Qy và có trị số:

y

r Q

Q S C



y x

Ixb

x

Thành phần r Q

có phương chiều phù hợp với lực cắt Qx và có trị số:

x

r Q

Q S C



x y

I y h

Thông thường, đối với các dầm dài khi tính ứng suất và biến dạng có thể bỏ qua ảnh hưởng của lực cắt so với ảnh hưởng của mô men uốn do đó trong các phần tính

x y

toán tiếp theo, ta không xét đến ảnh hưởng của ứng suất tiếp r Q ,r Q 

z

Thành phần r M 

có trị số và phương chiều phụ thuộc vào dạng tiết diện, với

tiết diện tròn thì ứng suất tiếp có phương vuông góc với bán kính, có chiều phù hợp với mô men xoắn nội lực Mz và có trị số:

M z

MZ 

I

(1.3)

P

1.2. THANH CHỊU UỐN XIÊN

1.2.1. Khái niệm

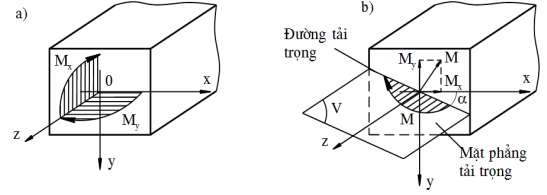
Hình 1.2:Thanh chịu uốn xiên

Thanh chịu uốn xiên (uốn không gian) khi thanh chịu uốn trong cả hai mặt phẳng quán tính chính. Ứng lực trên tiết diện, khi bỏ qua các lực cắt sẽ bao gồm mô men uốn Mx và mô men uốn My như hình vẽ 1.2a

Gọi M là vectơ tổng của các vectơ Mx và My, nằm trong mặt phẳng V chứa

trục z, nhưng không trùng với một mặt phẳng quán tính chính trung tâm nào. Giao tuyến của mặt phẳng này với mặt phẳng cắt ngang gọi là đường tải trọng. Trong uốn

xiên đường tải trọng đi qua trọng tâm nhưng không trùng với một trục quán tính trung tâm nào (hình 1.2b ).

1.2.2. Ứng suất pháp trên mặt cắt ngang

Theo nguyên lý cộng tác dụng, ứng suất pháp tại một điểm bất kì trên mặt cắt ngang (MCN) có toạ độ x, y được tính theo công thức:

z

M x y M y x

(1.4)

Ix I y

Trong đó Mx, My coi là dương khi làm căng phần chiều dương của trục y, trục x. Trong kĩ thuật người ta dùng công thức sau để không cần chú ý đến dấu của Mx,

My và toạ độ x, y:

M x

Ix

M y

I y

z y x

(1.5)

Ta sẽ chọn dấu “ + ” hoặc dấu “ - ” trước mỗi số hạng tuỳ theo các mômen uốn

Mx và My gây ra ứng suất kéo hay nén ở điểm đang xét.

Nếu gọi là góc của đường tải trọng hợp với trục x (hình 1.2b):

M M x M sin

tgx

M y M y M cos

Góc được gọi là dương khi quay từ chiều dương trục x đến đường tải trọng theo chiều kim đồng hồ.

1.2.3. Vị trí đường trung hoà

Từ (1.5) ta có phương trình đường trung hoà:

Hay:

M x y M y x  0

Ix I y

(1.6)

y M x . Ix .x tg.x

(1.7)

M y I y

Trong đó :

tgM x . Ix

M y I y

Hay:

tg

1 . Ix

(1.8)

tgI y

Đường trung hoà là một đường thẳng đi qua trọng tâm của mặt cắt ngang và không vuông góc với đường tải trọng như trong uốn phẳng.

Từ biểu thức (1.8) ta nhận thấy đối với các mặt cắt ngang có vô số hệ trục quán tính chính trung tâm như hình tròn, các đa giác đều cạnh sẽ có Ix= Iy nên tgtg= -1

thì không xảy ra hiện tượng uốn xiên phẳng. Vì đường tải trọng sẽ trùng với một trục quán tính chính trung tâm, còn đường trung hoà sẽ trùng với một trục quán tính chính trung tâm thứ hai vuông góc với đường tải trọng. Bài toán khi đó chỉ là uốn phẳng.

1.2.4. Biểu đồ ứng suất pháp trên mặt cắt ngang

Theo (1.5) mặt ứng suất là mặt phẳng, nên ứng suất pháp phân bố đều trên đường thẳng song song với đường trung hoà. Do đó ta có thể vẽ biểu đồ phân bố ứng suất pháp trên mặt cắt ngang trong hệ toạ độ như hình 1.3. Trục tung là đường trung hoà, trục hoành vuông góc với đường trung hoà.

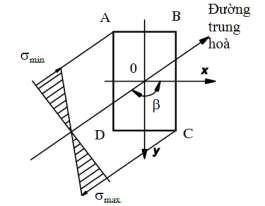
Hình 1.3: Biểu đồ ứng suất pháp trên MCN của dầm chịu uốn xiên

1.2.5. Điều kiện bền

Điểm nguy hiểm là các điểm xa đường trung hoà nhất về phía kéo hoặc nén.

Trạng thái ứng suất của điểm nguy hiểm là trạng thái ứng suất đơn.

max

Điều kiện bền có dạng:

- Đối với vật liệu dẻo:

- Đối với vật liệu giòn:



(1.9)

k



max



(1.10)

Trong đó:





M x

Ix

M y

I y

y x

min n

M x

Ix

M y

I y



; y x

(1.11)

max

k k min 



n n 



Nếu mặt cắt ngang của thanh là những mặt cắt có thể nội tiếp trong hình chữ nhật như hình 1.4 thì:

Do đó:

xk xn

xmax ;

yk yn

ymax

M x

M y

; (1.12)

max min

max

Wx Wy

Trong đó :

Wx x

I y

xmax

I

; Wy 

(1.13)

ymax

Trong trường hợp này điều kiện bền sẽ là:

- Đối với vật liệu dẻo:

Wx

- Đối với vật liệu giòn:



M x

M y

Wy

M x

M y

k



(1.14)

(1.15)

Wx Wy

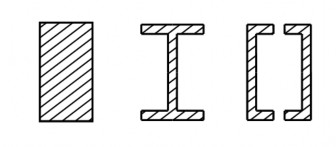
Hình 1.4: Một số mặt cắt nội tiếp hình chữ nhật

Từ điều kiện bền trên ta suy ra ba bài toán cơ bản sau:

- Bài toán kiểm tra bền

- Bài toán tìm tải trọng cho phép.

- Bài toán chọn kích thước MCN

Ví dụ 1.1

Một dầm công xon bằng gỗ, dài 2m, mặt cắt ngang hình chữ nhật (12  20) cm2, ở đầu tự do chịu lực tập trung P = 2,4 kN. Lực P đặt vuông góc với trục dầm và xiên góc = 30o với trục Oy (hình 1.5a).

Xác định vị trí đường tải trọng và ứng suất pháp ở các điểm góc A, B, C, D trên mặt cắt ngang ở ngàm.

Bài giải:

Phân tích lực P làm hai thành phần theo các trục Ox và Oy

Px P.sin2, 4 0, 5 1, 2 kN 

Py P. cos2, 4 0,866 2,08 kN 

Biểu đồ mô men uốn Mx và My được biểu diễn trên hình 1.5b,c. Vị trí đường tải trọng được xác định theo công thức:

tg = Mx Py l 2,08  1,732;

 60o .

My Px l

1,2

Mô men quán tính của mặt cắt ngang đối với các trục x và y

cm 

3 3

I x ;

12 12

3 3

cm 

I y ;

12 12