Kiểm Định Lựa Chọn Độ Trễ Tối Ưu Cho Mô Hình

hàng năm, mức lạm phát hàng ngày, chỉ số VNIndex…), và chuỗi các quan sát được thu thập trên cùng một đối tượng tại các mốc thời gian đều nhau được gọi là chuỗi thời gian3. Đối với việc phân tích hồi quy số liệu chuỗi thời gian, nếu mô hình hồi quy không chỉ bao gồm các giá trị hiện tại mà còn bao gồm các giá trị trễ (giá trị quá khứ) của các biến, mô hình đó được gọi là mô hình phân phối trễ. Nếu các biến giải thích của mô hình bao gồm một hay nhiều giá trị trễ của biến phụ thuộc, mô hình được gọi là mô hình tự hồi quy.

Mô hình VAR là mô hình vector tự hồi quy kết hợp giữa hai mô hình tự hồi quy đơn chiều (uinvariate autoregression – AR) và hệ phương trình đồng thời (simultaneous equations – Ses). VAR là một hệ thống các phương trình tuyến tính tất cả các biến số trong hệ thống đều được xem là biến nội sinh, mỗi phương trình (của từng biến nội sinh) trong hệ thống đều được giải thích bởi biến trễ của chính nó và các biến khác trong hệ thống. Mô hình VAR bao gồm nhiều dạng khác nhau như: mô hình VAR dạng rút gọn (reduced form VAR), dạng hệ qui (Recursive VAR), dạng cấu trúc (Structure VAR), dạng hiệu chỉnh sai số (Vector Error Correction). Xét về bản chất mô hình VAR được sử dụng phổ biến để ước lượng mối quan hệ giữa các biến kinh tế vĩ mô theo chuỗi thời gian dừng, có tác động qua lại và tác động này có tính trễ theo thời gian. Do đó, mô hình VAR không cần quan tâm đến tính nội sinh của các biến kinh tế trong mô hình, thông thường các biến kinh tế vĩ mô thường mang tính nội sinh nghĩa là tác động qua lại với nhau, điều này sẽ làm ảnh hưởng đến mức độ tin cậy của kết quả hồi quy đối với các phương pháp nghiên cứu hồi quy 1 phương trình đơn chiều.

Theo Nguyễn Quang Dong và Nguyễn Thị Minh (2013) thì trong mô hình Var, mỗi biến số được giải thích bằng một phương trình chứa các giá trị trễ của chính biến số và các giá trị trễ của các biến số khác. Mô hình Var được Christopher Sims (1999) sử dụng như mô hình không dựa trên lý thuyết kinh tế nào để nghiên cứu, và nó dự báo động thái của một số biến kinh tế. Mô hình Var dạng tổng quát (Svetlozar, Mittnik, Fabozzi, Focardi, Teo Jasic, 2007):

Y = A1Yt-1 + A2Yt-2 +....+ ApYt-p + st + ut (3.1)

3 Đôi khi các mốc này không thực sự cách đều nhau, ví dụ như chỉ số VNIndex bị gián đoạn bởi các ngày lễ và chủ nhật (Nguyễn Quang Dong và Nguyễn Thị Minh, 2013).

Trong đó: Yt = (Y1t , Y2t ,…Ynt) là chuỗi vector dòng (nx1) biến nội sinh theo chuỗi thời gian t, Ai ma trận hệ số (k x k) đối với i= 1,…, p của các biến nội sinh có độ trễ Yt-p; ut là sai số nhiễu trắng của các phương trình trong hệ thống có ma trận hiệp phương sai là ma trận đơn vị E(ut,ut’)=1; st = (s1t, s2t,...., smt) véctơ các yếu tố xác định, có thể bao gồm hằng số, xu thế tuyến tính hoặc đa thức.

Hay còn được viết lại là:

Yt = A0-1* A1Yt-1 + A0-1* A2Yt-2 + ... A0-1* ApYt-p + A0-1 ut (3.2) Yt = B1Yt-1 + B2Yt-2 + ... BpYt-p + et

Trong đó: Bs=A0-1As, s=1, 2, …, p và et=A0-1ut; et, ut là phần dư tương ứng của

các phương trình (3.1 và 3.2).

Mô hình VAR là một công cụ cơ bản trong phân tích kinh tế lượng với nhiều ứng dụng, ngoài ra mô hình VAR không đòi hỏi những chuỗi dữ liệu trong thời gian quá dài, vì vậy có thể sử dụng cho các nền kinh tế đang phát triển. Bên cạnh đó, mô hình VAR cũng có những tranh luận nhất định như khi số lượng quan sát đưa vào mô hình bị hạn chế thì có thể làm thay đổi độ trễ tối ưu của mô hình, và với những dữ liệu như nhau trong cùng khoảng thời gian nghiên cứu, nếu các nhà nghiên cứu có những giả định và luận giải khác nhau thì các kết quả nghiên cứu sẽ khác nhau.

Từ những ưu điểm của mô hình VAR, tác giả tiến hành nghiên cứu tuần tự theo các bước như sau:

(1) Các phép thử nghiệm đơn vị và đồng liên kết;

(2) Các kiểm định và ước lượng VAR;

(3) Các phép phân tích phân rã phương sai và các hàm phản ứng xung.

Ngoài việc cung cấp thông tin về tính chất thời gian của các biến, bước (1) đòi hỏi phải phân tích sơ bộ các chuỗi dữ liệu để xác định đúng đặc điểm của VAR trong bước (2). Trong khi đó, bước (3) đánh giá các kết quả ước tính của VAR.

Trong nghiên cứu này, đối với mục tiêu nghiên cứu thứ 2 là xem xét mối quan hệ giữa tăng trưởng kinh tế và vốn ĐTC trong lĩnh vực Nông nghiệp, Giao thông và CNTT&TT (MH2), nghiên cứu sử dụng mô hình VAR với phương pháp phân tích quan hệ nhân quả (Granger) được kế thừa từ các nghiên cứu vấn đề tương tự của Jibir và Abdu (2017), Gingo và Demireli (2018), Bakari (2018), Bakari, Fakraoui và Tiba (2019) nhằm xem xét tác động của ĐTC trong ba lĩnh vực trên đối với GDRP

của Tiền Giang. Lý do sử dụng mô hình VAR trong vấn đề này là vì mô hình này hỗ trợ việc phân tích tác động của các cú sốc ĐTC trong từng ngành đến tăng trưởng kinh tế tại Tiền Giang (tích hợp sẵn hàm phản ứng đẩy, phân rã phương sai…).

Mô hình hồi quy sẽ được xem xét lựa chọn sau khi tiến hành các kiểm định, đặc biệt là kiểm định tính dừng của các chuỗi thời gian bằng phương pháp phổ biến là Augmented Dickey-Fuller (ADF). Dữ liệu được sử dụng trong phân tích hàng quý 1998. Q1-2018.Q4, nếu dữ liệu chưa dừng thì sử dụng phương pháp sai phân để biến đổi. Kết quả lựa chọn độ trễ tối ưu cho mô hình được đánh giá dựa trên các tiêu chuẩn khác nhau như LR, FPE, AIC, SC, HQ. Trong nghiên cứu này tác giả căn cứ theo tiêu chuẩn thông dụng AIC. Kết quả kiểm định tính ổn định tổng quát của mô hình bằng nghiệm nghịch đảo của đa thức đặc tính AR cho thấy tất cả các nghiệm của đa thức đều nằm trong vòng tròn đơn vị, thì kết quả đạt được là mô hình VAR được ước lượng có tính ổn định.

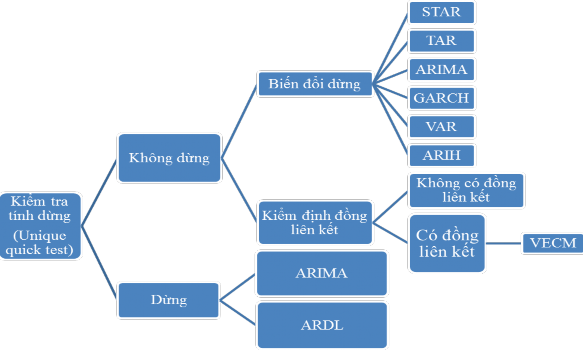
Nguồn: Tác giả tổng hợp theo Nguyễn Quang Dong và Nguyễn Thị Minh (2013)

Hình 3.2 Lựa chọn mô hình và các kiểm định hồi quy

3.2.2. Mô tả các biến của mô hình nghiên cứu

Đối với mục tiêu nghiên cứu 2 có bốn biến số, cụ thể là: Tăng trưởng kinh tế của Tiền Giang (GDRP) và vốn ĐTC trong ngành Nông nghiệp, Giao thông và CNTT&TT. Thực tế có thể có nhiều biến hơn nữa phù hợp cho phân tích. Tuy nhiên, mô hình mà tác giả sử dụng đòi hỏi phải có đủ số quan sát. Mô hình được xem xét có

ba biến số về ĐTC của ba ngành là những biến số đủ để quan sát tác động của ĐTC trong ba ngành chủ lực tác động đến tăng trưởng kinh tế tại Tiền Giang.

Bảng 3.3 Tổng hợp các biến số sử dụng trong mô hình

Biến số

Kí hiệu	Cách tính	Cơ sở chọn biến	Nguồn
Tăng trưởng kinh tế	LNGDRP	Ln_Tổng sản phẩm của Tiền Giang theo giá 2010	Keynes (1936), Solow (1956), Bakari (2018); Appiah (2018)	Cục Thống kê Tiền Giang, Sở Kế hoạch và Đầu tư Tiền Giang, Tổng Cục Thống kê Việt Nam
Vốn đầu tư trong lĩnh vực Nông nghiệp	LNDTNN	Ln_ Tổng vốn đầu tư trong lĩnh vực nông nghiệp
Vốn đầu tư trong lĩnh vực Giao thông	LNDTGT	Ln_ Tổng vốn đầu tư trong lĩnh vực giao thông
Vốn đầu tư trong lĩnh vực CNTT&TT	LNCNTT	Ln_ Tổng vốn đầu tư trong lĩnh vực CNTT&TT

Có thể bạn quan tâm!

Xem toàn bộ 180 trang tài liệu này.

Nguồn: Tác giả tổng hợp

3.2.3. Giả thuyết nghiên cứu

Vốn ĐTC trong lĩnh vực Nông nghiệp (LNDTNN), vốn ĐTC trong lĩnh vực Giao thông (LNDTGT) và vốn ĐTC trong lĩnh vực CNTT&TT (LNCNTT) có tác động đến tăng trưởng kinh tế tại Tiền Giang.

3.2.4. Dữ liệu nghiên cứu

Nghiên cứu sử dụng dữ liệu chuỗi thời gian gồm 84 đơn vị thời gian theo quí từ 1998.Q1 đến 2018.Q4. Dữ liệu được sử dụng trong nghiên cứu được tác giả tổng hợp và tính toán từ số liệu từ Cục Thống kê Tiền Giang, Sở Kế hoạch và Đầu tư Tiền Giang, Tổng Cục thống kê Việt Nam. Dữ liệu sau khi thu thập sẽ tiến hành tính toán cho các biến theo mô hình nghiên cứu. Hầu hết các biến đều có giá trị lớn là: GDP, vốn đầu tư trong ngành Nông nghiệp, Giao thông, CNTT&TT được lấy Ln trước khi đưa vào phân tích hồi qui.

Với mục đích kiểm tra nguồn vốn ĐTC vào từng ngành Nông nghiệp, Giao thông, CNTT&TT có tác động như thế nào đến GDRP của Tiền Giang.

3.2.5. Các kiểm định của mô hình

3.2.5.1 Tính dừng của các chuỗi dữ liệu

Dữ liệu của bất kỳ chuỗi thời gian có thể được xem là một quá trình ngẫu nhiên của một tập hợp dữ liệu cụ thể, được đo lường bởi kết quả của quá trình ngẫu nhiên

đó, tức là một mẫu của một tổng thể. Một dạng của quá trình ngẫu nhiên được các nhà phân tích về chuỗi thời gian đặc biệt quan tâm và xem xét kỹ lưỡng được gọi là quá trình ngẫu nhiên dừng.

Theo Nguyễn Quang Dong và Nguyễn Thị Minh (2013), một quá trình ngẫu nhiên hay một chuỗi thời gian Yt được coi là dừng nếu trung bình và phương sai của nó không đổi theo thời gian và giá trị của đồng phương sai giữa hai thời đoạn chỉ phụ thuộc vào khoảng cách, tức độ trễ về thời gian giữa hai thời đoạn này chứ không phụ thuộc vào thời điểm thực tế mà đồng phương sai được tính:

Trung bình: E (Yt) = µ

Phương sai: Var (Yt) = E (Yt - µ)2 = ϭ2 Đồng phương sai: γk = E [(Yt - µ) Yt+k - µ)]

Nếu trong hồi qui: Yt = β1t + β2t + ut, ut thực ra là dừng với trung bình bằng 0, và phương sai = ϭ2, thể hiện một chuỗi có xu hướng dừng TSP.

Theo Yaffee (2003), một chuỗi thời gian là dừng khi giá trị trung bình, phương sai, hiệp phương sai (tại các độ trễ khác nhau) giữ nguyên không đổi dù chuỗi được xác định vào thời điểm nào. Một chuỗi thời gian không dừng sẽ có giá trị trung bình thay đổi theo thời gian, hoặc giá trị phương sai thay đổi theo thời gian hoặc cả hai.

Theo Gujarati (2009), có nhiều phương pháp kiểm tra tính dừng của chuỗi thời gian: kiểm định Dickey–Fuller (DF), kiểm định Phillip–Person (PP), kiểm định Dickey và Fuller mở rộng (ADF), kiểm tra bằng giản đồ tự tương quan. Ngoài ra, phương pháp kiểm định nghiệm đơn vị cũng là một kiểm định thường được sử dụng để kiểm định một chuỗi thời gian là dừng hay không dừng. Dickey và Fuller (1981) đã đưa ra kiểm định Dickey và Fuller (DF) và kiểm định Dickey và Fuller mở rộng (ADF). Nghiên cứu này sử dụng kiểm định ADF để thực hiện kiểm định tính dừng của chuỗi dữ liệu, theo Dickey và Fuller (1981) mô hình kiểm định nghiệm đơn vị mở rộng ADF có dạng:

ΔYt = α0 + βYt–1 + ∑k∗ ∅j ∆Yt–1 + et (3.3)

j=1

ΔYt = α0 + δt + βYt–1 + ∑k ∗ ∅ j∆Yt–1 + et (3.4)

Trong đó: ΔYt = (Yt - Yt–1); Yt là chuỗi số liệu theo thời gian đang xem xét (t

= 1, 2….42 quan sát ); k là chiều dài độ trễ; et là nhiễu trắng

Mô hình (3.3) khác với mô hình (3.4) là có thêm biến xu hướng về thời gian t. Biến xu hướng là một biến có giá trị từ 1 đến n, trong đó 1 đại diện cho quan sát đầu tiên trong dữ liệu và n đại diện cho quan sát cuối cùng trong chuỗi dữ liệu. Nhiễu trắng là số hạng chỉ sai số ngẫu nhiên xuất phát từ các giả định cổ điển rằng nó có giá trị trung bình bằng 0, phương sai là hằng số và không tự tương quan. Giả thuyết kiểm định: H0: β = 0 (Yt là chuỗi dữ liệu không dừng).

Trong kiểm định ADF, giá trị kiểm định ADF không theo phân phối chuẩn. Theo Dickey và Fuller (1981), giá trị t ước lượng của các hệ số trong các mô hình (3.3) và (3.4) sẽ theo phân phối xác suất τ (τ = giá trị hệ số ước lượng/sai số của hệ số ước lượng). Giá trị tới hạn τ được xác định dựa trên bảng giá trị tính sẵn của MacKinnon (1996). Giá trị tới hạn này cũng được tính sẵn khi kiểm định ADF. Để kiểm định giả thuyết H0, nghiên cứu so sánh giá trị kiểm định τ tính toán với giá trị τ tới hạn của Mackinnon và kết luận về tính dừng của các chuỗi quan sát. Cụ thể, nếu trị tuyệt đối của giá trị tính toán lớn hơn trị tuyệt đối giá trị tới hạn thì giả thuyết H0 sẽ bị bác bỏ, tức chuỗi dữ liệu có tính dừng và ngược lại chấp nhận giả thuyết H0, tức dữ liệu không có tính dừng.

Một cách kiểm định tính dừng khác là kiểm định nghiệm đơn vị. Để tiến hành kiểm định này sẽ xem xét mô hình sau:

AR(1): Yt= Y t–1 + Ut Yt - Yt–1 = Ut

Tiếp đến sử dụng toán tử độ trễ L: LYt= Y t–1

(1-L) Yt = Ut. Thuật ngữ nghiệm đơn vị là để nói tới nghiệm của đa thức trong toán tử độ trễ.

Ở đây, Ut là số hạng chỉ sai số ngẫu nhiên xuất phát từ các giả định cổ điển rằng nó có giá trị trung bình bằng 0, phương sai ϭ2 là hằng số và không tự tương quan. Số hạng sai số này còn được biết tới dưới cái tên sai số nhiễu ngẫu nhiên (while noise error term). Nếu hệ số của Yt–1 trong thực tế bằng 1 thì chúng ta đang phải đối mặt với tình huống không dừng. Trong kinh tế lượng với chuỗi thời gian, một chuỗi thời gian có nghiệm đơn vị là kết quả của chuỗi thời gian không dừng. Nếu không có nghiệm đơn vị thì chuỗi thời gian thể hiện xu hướng xác định. Để biết được liệu chuỗi thời gian Yt có phải là chuỗi không dừng hay không, thực hiện hồi qui và kiểm tra xem L có bằng 1 về mặt thống kê hay không.

Tuy nhiên, nếu Yt được phát sinh từ: Yt - Yt–1 = α + ut; Với ut là dừng với trung bình bằng 0 và phương sai ϭ2, thì quá trình như thế là quá trình biến đổi sai phân của một chuỗi là dừng DSP. Nếu như một chuỗi thời gian được lấy sai phân một lần và chuỗi sai phân đó là dừng thì có thể nói rằng chuỗi ban đầu (dạng bước ngẫu nhiên) là một chuỗi kết hợp bậc 1 được ký hiệu là I(1): ΔYt = (Yt - Yt–1).

Như vậy, nếu một chuỗi thời gian được lấy sai phân d lần thì nó sẽ là chuỗi kết hợp bậc d, hoặc I(d). Theo qui ước, nếu d = 0 thì quá trình I(0) hệ quả sẽ thể hiện một chuỗi thời gian dừng.

Nếu một chuỗi dữ liệu không dừng thì sai phân của chuỗi có thể làm cho chuỗi dừng. Nếu một chuỗi không dừng và bắt đầu dừng ở sai phân bậc d thì được gọi là chuỗi liên kết bậc d. Ký hiệu: Yt ≈ I(d). Áp dụng phương pháp kiểm định nghiệm đơn vị Dickey – Fuller để kiểm định tính dừng cho lần lượt các chuỗi.

3.2.5.2 Kiểm định lựa chọn độ trễ tối ưu cho mô hình

Thông thường, có thể sử dụng biểu đồ PACF của phương pháp BOX – JENKIN hoặc sử dụng các tiêu chí LogL, AIC, SC để xác định độ trễ tối ưu cho mô hình. Kết quả của kiểm định ADF thường rất nhạy cảm với sự lựa chọn chiều dài độ trễ k nên tiêu chuẩn thông tin AIC (Akaike’s Information Criterion) của Akaike (1973) được sử dụng để chọn lựa k tối ưu cho mô hình ADF , giá trị k được lựa chọn sao cho AIC nhỏ nhất.

3.2.5.3 Kiểm định nhân quả Granger

Kiểm định nhân quả Granger (Granger, 1969) được sử dụng nhằm trả lời câu hỏi đơn giản là có hay không sự thay đổi của yếu tố này xảy ra bởi yếu tố khác và ngược lại. Trong nghiên cứu này, kiểm định Granger nhằm xem xét cho câu hỏi nghiên cứu là “Có hay không sự thay đổi của GDP dẫn đến sự thay đổi của vốn ĐTC trong lĩnh vực Nông nghiệp, Giao thông và CNTT&TT và ngược lại”.

Phương pháp hồi qui (Granger, 1969) có dạng:

Yt = α0 + ∑k βƖYt–1 + ∑k δ Ɩ Xt–1 + εt (3.5)

Ɩ=1 Ɩ=1

Yt = α1+ ∑k∅Ɩ Xt–1 + ∑kρƖYt–1 + υt(3.6)

Ɩ=1 Ɩ=1

Các trường hợp xảy ra khi kiểm định nhân quả Granger như sau:

- Nếu δ Ɩ ≠ 0 và có ý nghĩa thống kê nhưng ρƖ không có ý nghĩa thống kê, kết luận rằng sự biến động của X là nguyên nhân gây ra biến động của Y.

- Nếu δ Ɩ không có ý nghĩa thống kê nhưng ρƖ ≠ 0 và có ý nghĩa thống kê, kết luận rằng X chịu ảnh hưởng của sự biến động của Y.

- Nếu δ Ɩ và ρƖ đều khác 0 và không có ý nghĩa thống kê, kết luận rằng X và Y

độc lập với nhau.

- Nếu δ Ɩ và ρƖ đều khác 0 và có ý nghĩa thống kê, kết luận rằng X và Y tác

động qua lại lẫn nhau.

3.2.5.4 Kiểm định tính nhiễu trắng của phần dư

Phần dư của mô hình VAR phải là nhiễu trắng thì mô hình VAR mới có thể được sử dụng để dự báo.

3.2.5.5 Kiểm định tính ổn định của mô hình

Để kiểm định tính ổn định của mô hình VAR, sử dụng AR Root Test để xem xét các nghiệm hay các giá trị riêng đều nhỏ hơn 1 hoặc đều nằm trong vòng tròn đơn vị thì mô hình VAR đạt được tính ổn định.

3.2.5.6 Các phân tích trên mô hình VAR

Phân tích hàm phản ứng đẩy: Hàm phản ứng đẩy phát hiện phản ứng của các biến phụ thuộc trong hệ VAR đối với các cú sốc của các biến trong mô hình ở các giai đoạn tương lai.

Phân rã phương sai: Phân tích phân rã phương sai để phân tích mức độ tác động của yếu tố này đến yếu tố khác và ngược lại. Phân rã phương sai của sai số khi dự báo các biến trong mô hình VAR nghĩa là phân tách phần đóng góp của các chuỗi thời gian khác cũng như của chính chuỗi thời gian đó trong phương sai của sai số dự báo.

TÓM TẮT CHƯƠNG 3

Chương 3 đã đề cập đến phương pháp nghiên cứu để giải quyết các mục tiêu nghiên cứu của đề tài bằng cách trả lời câu hỏi nghiên cứu và các giả thuyết nghiên cứu. Đối với mục tiêu nghiên cứu 1: Nghiên cứu tiếp cận theo quy trình đánh giá hiệu quả quản lý ĐTC theo Rajaram (2010); Petrie, Murray (2010) và Vũ Thành Tự