Cơ Sở Lý Thuyết Xây Dựng Mô Hình Tính Toán Sức Kháng Cắt Dầm Btcđc Cst

thuộc chủ yếu vào dữ liệu thực tế, đầy đủ và đáng tin cậy. ANNs có thể giải quyết các vấn đề phi tuyến tính và phức tạp cao, bao gồm các vấn đề không chính xác và dữ liệu bị phân tán. Năm 2014 Naik và Kute đã phát triển mô hình ANNs dựa trên bảy và tám nút đầu vào để dự đoán khả năng chịu cắt của dầm sâu BT CĐC CST. Yassir M. Abbas, M. Iqbal Khan[103] đã phát triển mô hình ANN để tính toán cường độ chịu cắt tới hạn của dầm BTCST không cốt đai(sử dụng ANN 10). Mô hình ANN10 bào gồm 10 nút đầu vào, hai lớp ẩn, 14 nơ-ron, một đầu ra như Hình 2.24. Để đạt được kết quả mong muốn, trọng lượng (thể hiện sức mạnh kết nối giữa các nơ-ron) và sai lệch đã được điều chỉnh với tốc độ huấn luyện liên tục bằng cách sử dụng quy tắc học perceptron như được đưa ra bởi như 2.42. Sau đó, lỗi mạng (sự khác biệt giữa các mẫu đích được tính toán và dự kiến) đã được truyền lại từ lớp đầu ra sang lớp đầu vào. Quá trình điều chỉnh trọng lượng và nhận biết của nơ-ron đã được thực hiện cho đến khi hiệu quả đến được tại một mức độ chính xác.

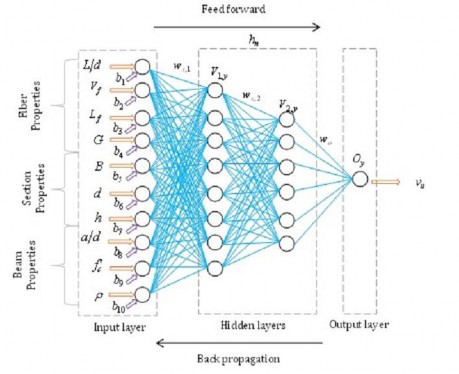
Hình 2.24 Cấu trúc của mạng ANN 10

Các nhà nghiên cứu đã sử dụng ANN cải tiến để điều tra ảnh hưởng của tỷ lệ nhịp cắt cắt tới khả năng chịu cắt của dầm sâu BTCĐC CST dầm. Họ báo cáo rằng ANNs là một kỹ thuật hứa hẹn để dự đoán hành vi cắt phức tạp của dầm BTCST theo

các thông số khác nhau, có thể làm giảm chi phí của các nghiên cứu thực nghiệm. Sử dụng bốn và năm nút đầu vào của ANNs, Adhikari và Mutsuyoshi (2006) dự đoán cường độ cắt tới hạn của dầm BTCSTdựa trên kết quả thực nghiệm. Đã có các nghiên cứu cho rằng kết quả dự báo của mạng tăng lên khi số nút đầu vào tăng lên. Ngoài ra, các tác giả quan sát thấy rằng mô hình ANNs có hiệu quả dự đoán tốt hơn so với phương pháp tính toán khác.

Xây dựng mô hình tính toán sức kháng cắt dầm BTCĐC CST

2.3.1. Cơ sở lý thuyết xây dựng mô hình tính toán sức kháng cắt dầm BTCĐC CST

Các mô hình lý thuyết kết hợp thực nghiệm (bán thực nghiệm) xem xét ứng xử cắt trên tiết diện nghiêng ở nhiều khía cạnh hơn. Nhiều mô hình bán thực nghiệm đã được lựa chọn tính toán sức kháng cắt cho dầm BTCST cường độ thường, có hoặc không cốt đai. Việc lựa chọn mô hình bán thực nghiệm phù hợp để dự báo sức kháng cắt của dầm BTCĐC CST là rất quan trọng. Mô hình bán thực nghiệm đó không những đánh giá đúng ứng xử cắt của dầm BTCĐC CST mà còn cho phép ta xem xét nhiều yếu tố ảnh hưởng đến sức kháng cắt của dầm nói trên. Mô hình bán thực nghiệm có thể cho ta biết rõ về ứng xử cắt của dầm như dự báo được vết nứt nghiêng, dự báo biến dạng trong cốt dọc chủ cũng như cốt đai…

Mô hình Trường trường nén sửa đổi (MCFT) hoặc sửa đổi đơn giản (SMCFT) là mô hình bán thực nghiệm phù hợp đã được lựa chọn để dự báo sức kháng cắt cho dầm BT CST. Đặc biệt sử dụng mô hình MCFT để tính toán về cắt cho dầm BTCĐC CST phù hợp hơn do tính chặt chẽ của nó. Sự đóng góp của sợi thép đối với sức kháng cắt trong mô hình MCFT có thể xem xét một cách độc lập.

Đối với dầm BTCST, đã có một số tác giả sử dụng mô hình này để dự báo sức kháng cắt. Theo các tác giả Fasheng Zhang, Yining Ding, Jing Xu, Yulin Zhang, Weiqing Zhu, Yunxing Shi [61], áp dụng mô hình MCFT dự báo sức kháng cắt cho BTCST thích hợp hơn dầm BTCT không sợi bởi vì quan hệ ứng suất biến dạng tuyến tính hơn trong phạm vi thời điểm đạt tới hạn khi kéo. Sự đóng góp của cốt sợi thép trong sức kháng cắt của dầm BTCST được cho là do sự cải thiện cường độ chịu kéo của bê tông và cường độ chịu kéo dư trong mô hình MCFT. Sự phá hoại của BTCSTcó

thể bị ảnh hưởng bởi ứng suất cục bộ xảy ra ở vết nứt hơn là ứng suất trung bình. Thành phần lực truyền qua vết nứt là do sức kháng kéo tuột của cốt sợi và sức kháng cắt trên toàn bề mặt vết nứt tại giao giữa cốt sợi thép và vết nứt chính [61].

Mô hình MCFT cho dầm BTCST bao gồm 15 phương trình gồm các phương trình cân bằng, phương trình tương thích biến dạng và các phương trình tương quan giữa ứng suất và biến dạng như Bảng 2.2.

Bảng 2.2 Phương trình tương thích biến dạng, các phương trình cân bằng trong mô hình và ứng suất biếng dạng MCFT cho đầm BTCST [61]

Ứng suất tại vết nứt

0.33 fc '

1 5001

Theo mô hình MCFT như mô tả ở bảng 2.2, sức kháng cắt của dầm BTCST phụ thuộc rất nhiều vào ứng suất kéo chính sau nứt (f1) của BTCĐC CST. Giá trị của ứng suất kéo chính (f1) bao gồm hai thành phần: phần ứng suất kéo của bê tông

( f1 

(1Vf )

và phần ứng suất kéo sau nứt(ứng suất kéo dư) của BTCST

sau nứt (σf). Như vậy, giá trị ứng suất kéo dư (σf) là phần đóng góp của cốt sợi thép trong ứng suất kéo chính (f1). Mô hình vật liệu của bê tông cốt sợi thép được đề xuất như Hình 2.25.

RC

Biến dạng khi kéo,%

Ứng suất kéo, Mpa

Hình 2.25 Mô hình ứng xử kéo của bê tông cốt sợi thép theo MCTF [112]

Bê tông sau khi nứt, cốt sợi thép tiếp tục chịu kéo vì vậy ứng suất kéo sau nứt của BTCST tiếp tục đóng góp cho sức cắt của dầm BTCST. Ứng suất kéo sau nứt (σf) của BTCST đã được một số nghiên cứu trước đây đề xuất thông qua thí nghiệm kéo trực tiếp hoặc kéo gián tiếp cho BTCST cường độ thường.

Đối với BTCĐC CST rất ít nghiên cứu thực nghiệm đưa ra được công thức tính ứng suất kéo sau nứt. Vì vậy, luận án nghiên cứu thực nghiêm để xác định được ứng suất kéo sau nứt(σf) của BT CĐC CST. Từ đó đưa ra được công thức tính toán ứng suất kéo chính (f1). Từ đó xây dựng mô hình tính ứng xuất cắt trung bình của dầm BTĐC CST.

Theo mô hình MCFT, cường độ chịu cắt trung bình(ν) của dầm BTCST là hàm số của ứng suất kéo chính (f1) được thể hiện như phương trình (2-60). Thực vậy, xét mặt cắt nghiêng tại vết nứt của dầm BTCST, sơ đồ phân bố ứng suất của một phần dầm BTCST như Hình 2.26. Trong hình vẽ này, đưa ra sự so sánh giữa tính toán ứng suất trung bình và tính toán ứng suất cục bộ có thực tại vết nứt. Phương hướng của vết nứt tới hạn được cho là phương của biến dạng chính. Với hai khuynh hướng ứng suất như hình (2-25)

z fz cosf1 cosfsycr v cosfci cosvci sinPf sinNA sin

Pf (cosf sin)NA cos

(2-56)

Có thể bạn quan tâm!

• So Sánh Cường Độ Chịu Cắt Thử Nghiệm Và Trong Tiêu Chuẩn Khi Tăng Cường Độ Chịu Nén Tới 100Mpa [102]
• Mô Hình Tính Toán Sức Kháng Cắt Theo Hai H. Dinh Và Cộng Sự [69]
• Xác Định Giá Trị  Và  Cho Các Dầm Không Chứa Cốt Thép Đai [60].
• Kế Hoạch Thí Nghiệm Xây Dựng Mô Hình Tính Toán Cường Độ Chịu Kéo Dư (Σf).
• Kết Quả Xử Lý Số Liệu Của Mẫu Sử Dụng Loại Sợi Ngắn (Lf/df=63.63)
• Bố Trí Cốt Thép Và Các Vị Trí Đo Biến Dạng Và Độ Võng Khi Uốn Dầm Btcđc Cst

Xem toàn bộ 184 trang tài liệu này.

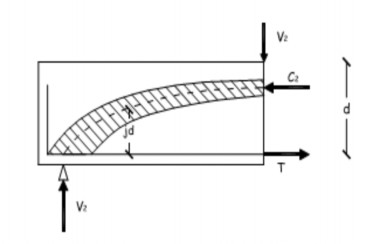
Thành phần cấu thành nên Pf song song với vết nứt f

Pf sinNA

và vuông

góc với vết nứt f Pf (cosf sin)NA thu được nhờ phân tích sự truyền ứng suất

giữa sợi và bê tông như Hình 2.26a. Khi đó phương trình (2-56) được đổi thành

z fsz cosf1 cosfszcr v cosfci c

f s inf cos

osvci sin(2-57)
Vết nứt a) b)	c)

Hình 2.26 Phân bố ứng suất trên tiết diện vết nứt nghiêng [61]

a) Thành phần ứng suất của sợi thép ngang qua vết nứt và song song với vết nứt,

b) ứng suất trung bình tính toán, c) Ứng suất cục bộ tại vết nứt

Yêu cầu hai trường hợp ứng suất trên mặt phẳng 1 cho kết quả như nhau theo phương x như sau phương trình (2-58):

x fxz sinf1 sinfsxcr v sinfci sinvci cosf s inf cos

(2-58)

Trong đó: Pf: Giá trị chịu lực trung bình của cốt sợi cắt qua vết nứt;

NA: Số sợi trên một đơn vị diện tích theo ba phương ( NA

vf )

2 d

f

α: Góc tạo bởi hướng của tải trọng và cốt sợi

fci : Ứng suất nén trên bề mặt vết nứt

vci : Ứng suất cắt trên bề mặt vết nứt

v f : Sự tham gia của lực Pf

song song với vết nứt ( vf

f (1f ))

Khi mà lực theo phương x và phương z thỏa mãn điều kiện cân bằng thì

fci =0;

Cho rằng phần tử sử dụng đưa ra sử dụng mô hình mặt cắt trong vùng cắt uốn trong

f1 'ci tanz fszcr

(2-59)

dầm, ứng suất kẹp như sau:

fz coi như rất nhỏ. Do vậy, có thể thu được phương trình (2-59)

Trong đó: 'ci ci f f cot; và 'ci : Là ứng suất cắt trên bề mặt vết nứt của dầm bê tông cốt sợi

Sự cân bằng, khả năng tương thích và các mối quan hệ cấu thành được xây

dựng dựa trên các ứng suất và biến dạng trung bình cho bê tông có được bằng cách đưa ra cơ chế truyền ứng suất tại giao cắt giữa sợi thép và vết nứt đầu tiên. Phương trình cường độ chịu cắt trung bình theo mô hình MCFT khi dầm có cốt đai như (2-60) và (2-61):

v f1 cotZ fszcr cot

(2-60)
v ' f cot ci z szcr	(2-61)

Đối với dầm BTCT không có cốt sợi thép: Ứng suất kéo chính trung bình sau khi nứt (f1) được Vecchio, F. J., và Collins, M. P., [112] đưa ra từ nghiên cứu thực nghiệm như phương trình(2-62).

f 0.33 fc ' (MPa)

1 1 500

1

(2-62)

Căn cứ vào các phương trình tính toán ứng suất cắt trung bình (2-60) có thể xây dựng mô hình tính toán cường độ chịu cắt trung bình cho dầm như phương trình (2-63):

v f 'c z fszcr cot(MPa)

(2-63)

Trong đó:

 0, 33cot 1

5001

Đối với BTCĐC CST ứng suất kéo chính (f1) theo mô hình MCFT trình bày ở bảng 2.2 bao gồm hai thành phần: phần đóng góp của bê tông CĐC và phần đóng góp của cốt sợi thép (σf) như phương trình (2-64). Phần đóng góp của bê tông

f 0.33 fc ' (1V )  1 1 500f f 1

(2-64)

được nhân với (1-Vf ) vì phải bỏ qua phần thể tích chiếm chỗ của cốt sợi thép trong bê tông.

Trong đó: f - là cường độ chịu kéo dư sau nứt của bê tông CĐC cốt sợi thép, MPa; V - là hàm lượng sợi tính theo%

Từ phương trình tính ứng suất kéo chính được đề xuất cho dầm BTCĐC CST

như phương trình (2-64), thay vào phương trình(2-60) ta được phương trình tính cường độ chịu cắt trung bình của dầm BTCĐC CST như (2-65):

 0, 33 f ' 

v c (1V ) f  cot

1 500f f z szcr 

1 

(2-65)

Có thể tách các thành phần đóng góp của bê tông, cốt sợi thép và cốt đai như (2-66). Trong đó để xét riêng phần ảnh hưởng của bê tông và cốt sợi thép hệ số β cần nhân thêm với (1-νf) để xét đến phần thể tích chiếm chỗ của sợi thép:

v f 'c f cotz fszcr cot

(2-66)
Trong đó:  0.33cot(1V ) 1 500f 1	(2-67)

Ứng xử cắt của dầm BTCST, đặc biệt là dầm ngắn, có thể ảnh hưởng bởi một phần bởi hiệu ứng vòm và một phần bởi hiệu ứng dầm. Giải quyết cơ chế truyền lực cắt của dầm BTCST cần xem xét đến hiệu ứng dầm và hiệu ứng vòm. Sự đóng góp sức kháng cắt trong cơ cấu vòm cần được đáng giá và được thể hiện theo cơ chế như Hình 2.26. Tác động của hiệu ứng vòm là đáng kể khi tỷ số a /d <2.5. Khi đó, ứng suất cắt cần được điều chỉnh bởi hệ số do dv có giá trị thay đổi tùy theo vị trí mặt cắt. Đối với dầm ngắn (a /d <2.5), hiệu ứng vòm được xem xét bằng cách nhân phần đóng góp của bê tông với 2.5d/a.

Hình 2.27 Hiệu ứng vòm trong dầm BTCST

Vì vậy ứng suất cắt trung bình của dầm BTCST được đề xuất như (2-68) và (2-69) cho hai trường hợp nêu trên.

v fc ' f cotz fszcr cot, khi a/d≥2.5;

(2-68)
v  2.5d / a[fc ' f cotz fszcr cot], khi a/d<2.5;	(2-69)

Góc nghiêng của ứng suất kéo chính (θ) được xem là thay đổi tùy theo biến dạng theo phương dọc trục dầm (Ɛx) như ở phương trình (2-55). Đặc biệt trong dầm BTCST có sử dụng cốt đai, ứng xử của vết nứt nghiêng như góc nghiêng của vết nứt phụ thuộc nhiều yếu tố. Tuy nhiên, để đơn giản hơn trong tính toán, có thể sử dụng phương pháp trong mô hình trường nén sửa đổi đơn giản cho dầm BTCĐC CST.

Mô hình trường nén sửa đổi đơn giản (SMCFT) như đã phân tích cho phép tính hệ số β độc lập với góc θ. Với giá trị của Sxe=300mm, phương trình (2-55) cho phép tính giá trị góc nghiêng của ứng suất nén chính (θ) như phương trình (2-70) và đã được đưa vào tiêu chuẩn AASHTO-2017 [43]

 29  7000x

(2-70)

Hệ số xét đến ảnh hưởng của ứng suất kéo của bê tông sau nứt được lấy theo mô hình trường nén sửa đổi đơn giản từ phương trình (2-54), với việc lấy giá trị của Sxe=300mm thu được phương trình (2-71). Tham số (1-Vf) được đưa vào để bỏ qua phần thể tích của cốt sợi thép trong bê tông(vì cụm phương trình này là đóng góp của riêng phần bê tông)

Xem tất cả 184 trang.