Kế Hoạch Thí Nghiệm Xây Dựng Mô Hình Tính Toán Cường Độ Chịu Kéo Dư (Σf).

0.4 (1V ) 11500f

(2-71)

Có thể bạn quan tâm!

Trong phương trình (2-70), cho thấy góc nghiêng của vết nứt phụ thuộc vào biến dạng theo phương dọc trục dầm hay phụ thuộc vào biến dạng trong cốt dọc chủ (Ɛs). Theo đề xuất trong tiêu chuẩn TCVN11823-2017 đề xuất tính biến dạng theo phương này cho dầm BTCT thường không dự ứng lực, như phương trình (2-72). Tuy nhiên với sự tham gia của cốt sợi thép, biến dạng trong cốt thép dọc bị ảnh hưởng. Do mô men tại tiết diện có thêm thành phần đóng góp của cốt sợi thép như ở phương trình(2-73) và biến dạng trong cốt dọc được tính toán lại như(2-74).

M u V

du

v

s A E

s s

(2-72)

M b(h e)( h e a )

(2-73)

f t

Trong đó:

2 2 2

e = (s+0.003)c/0.003, mm

t = 0.00772Lf/DffFbe, MPa Lf - chiều dài của sợi thép, mm

Df - đường kính của sợi thép, mm

f - thể tích sợi thép, %

a - chiều cao khối ứng suất quy ước ở miền chịu nén, mm b - chiều rộng của dầm, mm

c - Chiều cao miền bê tông chịu nén, mm d - Chiều cao hữu hiệu của dầm, mm

e - khoảng cách từ mép trên khối ứng suất kéo(do cốt sợi) đến thớ chịu nén xa nhất, mm

s - biến dạng của sợi thép theo lý thuyết cân bằng mô men trong dầm, s = s/Es, quy định s=2.3MPa

f’c - cường độ chịu nén của bê tông, MPa

fy - giới hạn chảy trong các thanh tăng cường, MPa

C - Lực nén trong bê tông, N h - chiều cao của dầm, mm

t - ứng suất kéo trong BTCST, MPa Es - mô đun đàn hồi của BTCST, MPa

Tfc - lực kéo trong BTCST Tfc = tb (h - e), N Trb - lực kéo trong cốt thép tăng cường = Asfy, N

Trong bài toán thiết kế cốt đai cho dầm BTCĐC CST, do miền bê tông chịu kéo có phần đóng góp của cốt sợi thép nên công thức tính toán biến dạng trong cốt dọc chủ như (2-74)

Mu M f V

dv

s A E

s s

(2-74)

Từ mô hình bán thực nghiệm như đã đề xuất trong công thức (2-69) và (2-68), cho thấy phần đóng góp cho sức kháng cắt dầm BTCĐC CST chính là ứng suất kéo dư (f). Theo các nghiên cứu thực nghiệm đã chỉ ra trên, ứng suất kéo dư phụ thuộc vào cấp bê tông, loại sợi thép, hình dạng sợi, tỷ lệ hương sợi, hàm lượng sợi …Các tác giả Fasheng Zhang, Yining Ding, Jing Xu, Yulin Zhang, Weiqing Zhu, Yunxing Shi [100] đã đề xuất được công thức tính toán toán ứng suất kéo dư (f) cho BTCST cấp thông thường. Trong công thức đề xuất bởi tác giả nêu trên thì giá trị của f phụ thuộc vào hàm lượng sợi, tỷ số hình dạng và lực dính bám giữa sợi thép và bê tông. Việc thí nghiệm xác định dính bám giữa các loại sợi và bê tông ít được thực hiện nên số liệu không được công bố nhiều. Tuy nhiên, với BTCĐC dính bám giữa sợi thép và bê tông tốt hơn. Chưa nhiều công bố ứng suất kéo sau nứt cho riêng BTCĐC.

Việc xác định sự đóng góp của cốt sợi thép cho cường độ chịu kéo sau nứt của BTCĐC CST có thể thông qua thí nghiệm kéo trực tiếp hoặc ép chẻ. Tuy nhiên kéo trực tiếp gặp khó khăn về mặt thiết bị và khó thực hiện nên ta có thể dùng phương pháp ép chẻ.

Vì cường độ chịu kéo trực tiếp có thể tính được thông qua cường độ ép chẻ bằng cách nhân hệ số như trong tiêu chuẩn ACI 544-4R [32] đã chỉ ra. Do vậy, có thể dùng

thực nghiệm ép chẻ để đánh giá được đóng góp của cốt sợi thép trong cường độ chịu kéo. Từ kết quả thí nghiệm ép chẻ (kéo gián tiếp) tách phần đóng góp của riêng cốt sợi thép. Từ đó, có thể đưa ra được phần tham gia chịu kéo sau nứt của riêng cốt sợi thép (chính là f). Phần thực nghiệm được trình bày ở mục 2.3.2.

2.3.2. Kế hoạch thí nghiệm xây dựng mô hình tính toán cường độ chịu kéo dư (σf).

2.3.2.1. Trình tự thí nghiệm

- Xác định hàm mục tiêu và các yếu tố ảnh hưởng

- Xác định số lượng mẫu và lập kế hoạch thí nghiệm

- Tiến hành thí nghiệm

- Tổng hợp và phân tích kết quả thí nghiệm

- Xác định và đánh giá mối tương quan hồi quy giữa hàm mục tiêu và biến yếu tố đầu vào.

2.3.2.2. Xác định hàm mục tiêu các yếu tố ảnh hưởng

- Hàm mục tiêu

Mục đích quan trọng nhất của nghiên cứu thực nghiệm là xây dựng được hàm mục tiêu. Xây dựng hàm mục tiêu quan hệ với các thông số đầu vào sao cho biểu diễn gần đúng nhất với tập dữ liệu thí nghiệm. Phương trình này được gọi là phương trình hồi quy. Ở mức độ cơ bản, ta sử dụng phương trình hồi quy bậc nhất. Phương trình hồi quy bậc nhất có dạng một hàm bậc nhất, một biến. Có nhiều thông số ảnh hưởng đến ứng suất kéo sau nứt của BTCST như đã trình bày ở trên. Trong đó, hàm lượng sợi là thông số quan trọng vì nó làm tăng đáng kể cường độ chịu kéo cho bê tông. Vì vậy hàm mục tiêu trong thực nghiệm này là hàm quan hệ cường độ chịu ép chẻ (fsp) và hàm lượng sợi thép (Vf). Ngoài ra một số tham số khác như: tỷ lệ hình dạng sợi (Lf/Df) và cường độ chịu nén của bê tông (f’c) được xem như cố định.

- Xác định hệ số hồi quy

Khi ta thực hiện n giá trị thí nghiệm, để khảo sát sự phụ thuộc của cường độ chịu ép chẻ của BTCST vào biến số là hàm lượng sợi. Ta biểu diễn mối quan hệ giữa cường độ chịu ép chẻ (fsp) và hàm lượng sợi thép (Vf) dưới dạng bậc nhất như sau:

fsp= A + B. Vf;

(2-75)

Trong đó A và B là các hệ số hồi quy. Chúng ta chỉ có thể lập được phương trình hồi quy mà biểu diễn gần đúng nhất với tập dữ liệu thí nghiệm. Với phương trình hồi quy như (2-75) mỗi giá trị của hàm lượng sợi, tính được một giá trị của cường độ chịu ép chẻ khác với thí nghiệm. Mong muốn là làm sao sai khác giữa giá trị tính ra theo phương trình hồi quy và giá trị thí nghiệm là nhỏ nhất như công thức

(3) ở phụ lục 3. Cách tốt nhất là dùng phương pháp sai số bình phương tối thiểu(xem phụ lục 3). Phương pháp này được thực hiện như sau:

+ Tính trung bình của các giá trị fsp và νf

+ Tính số dư mô hình theo phương trình (4),(5), (6)của Phụ lục 3

+ Tính các hệ số A và B theo các phương trình (7) và (8)theo phụ lục 3

- Đánh giá sai số hồi quy

Để đánh giá được mức độ chính xác của mô hình hồi quy tìm được so với kết quả thí nghiệm, ta sử dụng hệ số đánh giá quyết định r2 theo như phương trình (9) Phụ lục 3.

Giá trị của r2 nằm trong khoảng 0 < r2 < 1. Nếu giá tri r2 chứng tỏ các số liệu tìm được hoặc chưa đủ để có được mô hình hồi quy đúng đắn, hoặc còn quá nhiều sai số thu thập dữ liệu. Giá trị r2 lớn chứng tỏ các dữ liệu thu thập được khá tốt để dụng được mô hình hồi quy có ít sai lệch với thực nghiệm.

Với mục tiêu nêu trên, NCS thiết kế thực nghiệm để xác định cường độ chịu ép chẻ của các tổ hợp mẫu trụ bê tông cốt sợi thép DRAMIX cho hai loại sợi có chiều dài khác nhau. Hàm lượng sợi thay đổi từ 0% đến 2%. Số lượng mẫu được quy định theo tiêu chuẩn ACI 318-11 gồm của 105 mẫu trụ kéo gián tiếp (ép chẻ) và 21 mẫu nén để để kiểm tra cấp bê tông (f’c). Các thông số đầu vào là cường độ bê tông (f’c), hàm lượng sợi (Vf), tỷ lệ hình dạng sợi (Lf/Df). Căn cứ vào kết quả thí nghiệm, xây dựng công thức xác định cường độ chịu ép chẻ (kéo bửa) của BTCĐC CST theo biến số là hàm lượng sợi(Vf), các tham số khác được xem là cố định. Sử dụng phần mềm Minitab V17 để xử lý và đưa ra hàm hồi quy tuyến tính liên quan giữa cường độ chịu kéo gián tiếp (ép chẻ) với hàm lượng sợi thép (Vf) với mục tiêu nêu trên. Mô hình sẽ được trình bày dưới dạng tách riêng phần tham gia của bê tông và phần tham gia của cốt sợi thép. Qua đó, xác định được ứng suất kéo dư của BTCST.

f '

Trước đây, đã có một số nghiên cứu thực nghiệm về cường độ chịu kéo của BTCST đề xuất mô hình bậc nhất để dự báo cường độ ép chẻ BTCST theo hàm lượng sợi thép và các thông số khác như cường độ chịu nén và tỷ lệ kích thước của sợi thép. Mazen Musmar (2013) đã đề xuất mô hình tính toán cường độ chịu kéo như ở phương

trình (2-76). Trong mô hình này phần đóng góp của bê tông ( 0.6

f '

) và phần đóng

góp của riêng cốt sợi thép ( 0.4 f

bê tông cấp thông thường.

).Tuy nhiên đây mới chỉ là thử nghiệm cho

f  0.6 f '  0.4 f V f '

sp c D f c

(2-76)

Đối với phần đóng góp của bê tông, theo các tác giả Phạm Duy Hữu, Đào Văn Đông, Phạm Duy Anh [13] và theo tiêu chuẩn ACI 363R - 92[30] thì cường độ chịu ép chẻ của bê tông cấp 21 - 83 MPa có tương quan với cường độ chịu nén như phương trình (2-79).

f  0.59 f '

sp c

(2-77)

Cường độ chịu ép chẻ của riêng bê tông phụ thuộc cấp bê tông có giá trị như phương trình (2-77) [15], [93]. Đối với BTCST, phần còn lại trong phương trình (2-76) chính là đóng góp của cốt sợi thép cho ứng suất kéo sau nứt. Do đó, thông qua thí nghiệm ép chẻ mẫu BTCĐCST phần đóng góp của riêng cốt sợi thép cho cường độ chịu kéo hoàn toàn có thể xác định được.

2.3.2.3. Số lượng mẫu thí nghiệm

Số lượng mẫu thí nghiệm phụ thuộc vào số lượng cấp phối bê tông lựa chọn. Xác định cỡ mẫu trong một tổ mẫu thí nghiệm được tính toán nhằm ước đoán trung bình của một tập dữ liệu với mức ý nghĩa α = 0.05 và năng lực thống kê lớn hơn 80% với hy vọng dự đoán được giá trị trung bình sai khác so với thực tế không quá

1.5 lần độ lệch chuẩn (δ = 1.5σ). Bằng phần mềm Minitab V17 tính toán được cỡ mẫu đảm bảo các điều kiện trên được thể hiện ở Bảng 2.3 và Hình 2.28.

Bảng 2.3 Kết quả tính toán số lượng mẫu trong một tổ mẫu bằng Minitab V17

Power and Sample Size

Sample

1-Sample t Test

Difference

Size

Power

Testing mean = null (versus ≠ null) Calculating power for mean = null + difference α = 0.05

Assumed standard deviation = 1

1.5

0.832529

0.999684

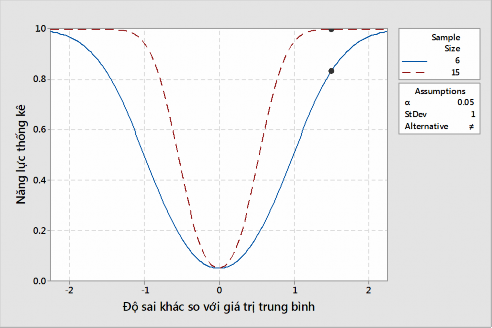
Hình 2.28. Môi quan hệ giữa năng lực thống kê phụ thuộc theo cỡ mẫu và độ sai khác so với giá trị trung bình

Từ kết quả trên tiến hành lập kế hoạch thí nghiệm với số lượng mẫu thí nghiệm được thể hiện ở bảng 2.4. Riêng mẫu nén xác định cường độ chịu nén dùng mẫu kích thước D*H = 10cm*20cm (do năng lực máy nén hạn chế).

Bảng 2.4 Số lượng và kích thước mẫu ép chẻ và mẫu nén

Loại hỗn hợp

Hàm lượng sợi (%)	Loại sợi, chiều dài sợi, mm	Số lượng mẫu xác định cường độ ép chẻ (DH=1530cm)	Số mẫu xác định cường độ nén (DH=1020)	Tổng số mẫu hình trụ 1530 cm và 1020cm	Tiêu chuẩn
CP0-F'C70	0		15	3	126	ACI 318-11
CP1-S1- F'C70	0.63	Dramix 3D 65/35 BG	15	3
CP1-S2- F'C70	0.63	Dramix 3D 80/60 BG	15	3
CP2-S1- F'C70	1	Dramix 3D 65/35 BG	15	3
CP2-S2- F'C70	1	Dramix 3D 80/60 BG	15	3
CP3-S1- F'C70	1.5	Dramix 3D 65/35 BG	15	3
CP3-S2- F'C70	1.5	Dramix 3D 80/60 BG	15	3
		Tổng số mẫu	105	21

2.3.2.4. Phân tích kết quả xây dựng hàm mục tiêu

Quá trình thí nghiệm mẫu được trình bày ở phụ lục 2. Kết quả cường độ chịu ép chẻ của 105 mẫu bê tông cường độ cao cốt sợi thép(kích thước D*H = 15cm*30cm) của các hỗn hợp BTCST thu được như bảng 1 phụ lục 2.

Các kết quả thí nghiệm được phân tích thống kê, hàm mật độ xác suất các mẫu thí nghiệm ứng với các trường hợp không có sợi, sợi ngắn và sợi dài với các hàm lượng sợi khác nhau được thể hiện ở Hình 2.29, Hình 2.30 và Hình 2.31. Thông qua các hàm mật độ xác suất và các tham số thông kê như độ lệch chuẩn, hệ số phân tán cho thấy các kết quả cường độ chịu ép chẻ là các đều là các đại lượng ngẫu nhiên liên tục phân bố theo đúng quy luật phân phối chuẩn, các kết quả thí nghiệm với độ lệch chuẩn nhỏ từ 0.33-1.18 MPa phân phối đều đặn xung quanh giá trị trung bình. Điều này cho thấy việc thí nghiệm xác định chỉ tiêu cường độ ép chẻ đạt yêu cầu về độ chụm.

1.2

1.0

0.8

Variable Không sợi N-0.63% N-1%

N-1.5%

Mean StDev N 5.679 0.8135 15

6.929 0.3259 15

8.201 0.5231 12

10.15 0.6115 12

0.6

0.4

0.2

0.0

Cường độ é p chẻ (MPa)

0.8

0.7

0.6

0.5

Variable 0%

D-0.63% D-1%

D-1.5%

Mean StDev N 5.679 0.8135 15

8.484 0.6956 15

9.401 0.5639 12

11.39 1.184 12

0.4

0.3

0.2

0.1

0.0

Cường độ ép chẻ (MPa)

Mật độ

Hình 2.29. Hàm phân phối chuẩn cường độ ép chẻ của mẫu không sợi và sợi ngắn

1.2

1.0

0.8

0.6

Variable N-0.63% N-1%

N-1.5% D-0.63% D-1%

D-1.5%

Mean StDev N 6.929 0.3259 15

8.201 0.5231 12

10.15 0.6115 12

8.484 0.6956 15

9.401 0.5639 12

11.39 1.184 12

0.4

0.2

0.0

Cường độ ép chẻ (MPa)

Mật độ

Hình 2.30. Hàm phân phối chuẩn cường độ ép chẻ của mẫu không sợi và sợi dài

Hình 2.31. Hàm phân phối chuẩn cường độ ép chẻ của mẫu sợi ngắn và sợi dài

Xem tất cả 184 trang.

Ngày đăng: 22/10/2023