trong đó:
(t) s(t),e(t)T.
s(t) : là khoảng cách along-track. e(t): là sai số bám quỹ đạo.
Theo tài liệu [31] thì giá trị ma trận
R p (k ) được tính như sau:
R a
Tcos ak
sin ak
T
(3.55)
p k sin a cos a
k k
Ta có thể xác định được sai số bám quỹ đạo của con tàu như sau:
et xt xk sin aky t yk cos ak
(3.56)
Nhiệm vụ chính của hệ thống dẫn đường (Guidance) là tính toán các trạng thái mong muốn giúp cho AUV bám theo quỹ đạo được định trước, điều này cũng tương đương với việc hệ thống dẫn đường phải làm cho sai số bám quỹ đạo e(t) tiến về 0 ( lim e(t) 0 ). Để thực hiện được điều này thì hệ thống
t
dẫn đường LOS sử dụng nguyên lý Lookahead-based Steering để tính toán
hướng đi mong muốn d
và từ đó tính ra góc mũi tàu mong muốn d
cung
cấp cho hệ thống máy lái tự động. Hệ thống máy lái tự động sẽ sử dụng d như là tín hiệu điều khiển đầu vào nhằm điều khiển con tàu bám theo quỹ đạo mong muốn và làm cho sai số bám quỹ đạo của con tàu giảm dần về 0.
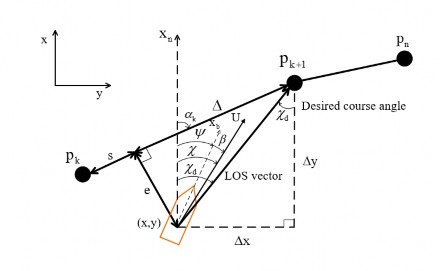
Hình 3.10 Luật điều hướng LOS
Phương pháp điều khiển tàu bằng nguyên lý Lookahead-based Steering sẽ làm cho sai số bám quỹ đạo e(t) tiến về 0 bằng cách hướng vector vận tốc của AUV đến điểm chuyển hướng kế tiếp trên quỹ đạo mà con tàu cần phải
k1
đi đến hay cũng chính là điểm chuyển hướng pn trên đoạn thẳng quỹ đạo mà
con tàu đang bám theo như hình 3.10.
Theo tài liệu [31] thì hướng đi mong muốn d
theo nguyên lý
Lookahead-based Steering sẽ được tách thành hai thành phần như sau:
d p r e
(3.57)
Trong đó p
là góc tiếp tuyến của đoạn thẳng quỹ đạo mong muốn còn
r là góc tương quan giữa vận tốc và quỹ đạo chuyển. Góc r được thêm vào
n
d nhằm đảm bảo rằng vector vận tốc U của con tàu luôn hướng về điểm
p
chuyển hướng
k1 .
p ak
(3.58)
𝜒𝑟
(𝑒) = 𝑎𝑟𝑐𝑡𝑎𝑛 (− 𝑒(𝑡) ) (3.59)
Δ
Trong đó
là khoảng cách từ hình chiếu của điểm
pn (t)
trên đoạn
p
thẳng quỹ đạo mong muốn cho đến điểm chuyển hướng
n k1
.
Từ (3.57), (3.58) và (3.59) thì ta có thể tính được hướng đi mong muốn (desired heading) theo nguyên lý Lookahead-based Steering như sau:
d d p r
(3.60)
Trong đó
arcsin v
U
là góc trượt của con tàu. Tuy nhiên vì v U
nên ta có thể giả thiết như 0 .
Khi đó (3.60) được viết lại thành:
d p r e
(3.61)
Khoảng cách từ vị trí AUV đến điểm chuyển hướng được tính như sau:
x xt2y y t2R2
(3.62)
n n n
Đây là điều kiện để AUV chuyển sang điểm chuyển hướng tiếp theo. Trong trường hợp không gian 3 chiều (3D), độ sâu điểm chuyển hướng được tính đến:
𝑛
[𝑥𝑛 − 𝑥(𝑡)]2 + [𝑦𝑛 − 𝑦(𝑡)]2 + [𝑧𝑛 − 𝑧(𝑡)]2 ≤ 𝑅2 (3.63)
Trong đề tài này, tác giả điều khiển AUV theo quỹ đạo vuông góc và zig-zag. Các kết quả mô phỏng được trình bày ở Chương 4.
3.4.2 Điều khiển AUV bám theo địa hình đáy
Trong hoạt động này, AUV có thể chuyển động thẳng hoặc chuyển hướng nhưng luôn giữ một độ sâu nhất định so với đáy ở vị trí hiện tại. Giá trị độ sâu mong muốn mà hệ thống điều khiển độ sâu nhận được phụ thuộc vào độ sâu đo được từ máy đo sâu hồi âm. Vị trí của AUV theo chiều thẳng đứng thay đổi theo địa hình đáy.
Thực chất trong nghiên cứu này, bộ điều khiển sẽ giúp AUV bám theo giá trị độ sâu mong muốn khi độ sâu thay đổi. Hàm mục tiêu của trường hợp này giống như tình huống điều khiển độ sâu đơn thuần nhưng điểm đặt thay đổi liên tục trong khi bộ điều khiển hướng và tốc độ giữ ổn định hướng đi và tốc độ mong muốn.
3.5 Các phương án thích nghi cho hệ thống điều khiển AUV
3.5.1 Mô hình dòng chảy tác động lên AUV
Đề tài sử dụng mô hình dòng chảy 3 chiều (Fossen, 2002) [31]. Các thành phần dòng chảy theo hệ tọa độ cố định trên trái đất được mô tả bởi hai tham số là: vận tốc dòng chảy trung bình 𝑉𝑐 và hướng dòng chảy 𝛾𝑐, góc thẳng
đứng của dòng chảy là 𝑐.
Các thành phần của hệ tọa độ cố định trên vật thể (AUV) được tính từ:
𝑢𝑐= 𝑉𝑐𝑐os(𝛾𝑐− 𝜓)
𝑣𝑐 = 𝑉𝑐 𝑠𝑖𝑛(𝛾𝑐 − 𝜓)
𝑤𝑐 = 𝑉𝑐 𝑐𝑜𝑠(𝑐 − ) (3.65)
𝑉𝑐 = √𝑢2 + 𝑣2 + 𝑤2
𝑐 𝑐 𝑐
Vận tốc dòng chảy trung bình cho mô phỏng được tạo ra bằng cách sử dụng phương pháp Gauss – Markov bậc nhất như sau:
dVc t V
t t
(3.66)
dt 0 c
trong đó, 𝜔(𝑡)là một chuỗi nhiễu trắng Gaussian và 𝜇0 ≥ 0 là một hằng số. Nếu 𝜇0 = 0, mô hình dòng chảy này rút gọn thành bước đi ngẫu nhiên (random walk) tương ứng với tích phân nhiễu trắng theo thời gian. Một phần tử bão hòa thường được sử dụng trong quá trình tích phân để giới hạn vận tốc dòng chảy:
Vmin Vc tVmax
(3.67)
Với các số liệu dòng chảy cụ thể, ba thành phần vận tốc dòng chảy theo 3 trục tọa độ được đưa vào chuyển động của AUV trong chương trình mô phỏng. Ba thành phần của dòng chảy đó được tính theo các phương trình (3.65).
3.5.2 Thích nghi với tác động của dòng chảy
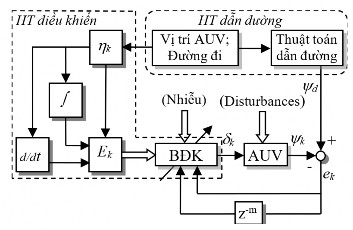
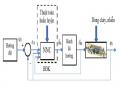
Hình 3.51 Sơ đồ hệ thống điều khiển AUV theo quỹ đạo tính đến độ dạt do dòng chảy gây ra.
Hình 3.11 Mô tả sơ đồ hệ thống điều khiển AUV theo quỹ đạo đặt trước. Hàm mục tiêu Ek để huấn luyện mạng nơ-ron điều khiển được điều chỉnh. Tác giả dựa theo phương pháp giới thiệu trong [3], khoảng cách dạt khỏi đường đi mong muốn (d) trên mặt phẳng ngang và dấu của khoảng cách
này có thể xác định được. Định nghĩa giá trị khoảng cách này theo chiều dài thân tàu là = d/L, trong đó L là chiều dài thân tàu tính bằng mét.
Hàm mục tiêu sẽ có dạng sau đây:
𝐸 = 1 [𝜌 (𝜓𝑑 − 𝜓
)2 + 𝜌 (𝜂𝑑 − 𝜂
)2 + 𝜆𝛿2 + 𝜎𝑟2] , (3.68)
𝑘 2 1 𝑘 𝑘
2 𝑘 𝑘
𝑘 𝑘
d
d
trong đó k và k lần lượt là hướng đi mong muốn và hướng đi thực tế của AUV trên mặt phẳng ngang; k và k là giá trị độ dạt khỏi đường đi mong
k
muốn và thực tế; k là góc bánh lái hướng; rk là tốc độ thay đổi hướng ( r
k);
1, 2, , lần lượt là các hệ số dương. Gọi sai số hướng đi AUV là:
𝑘
𝑒𝑘 = 𝜓𝑑 − 𝜓𝑘 (3.69)
𝑘
Và chú ý là giá trị độ dạt khỏi đường đi cần đạt được là 𝜂𝑑 = 0, hàm
mục tiêu lúc này sẽ trở thành:
1 2 2 2 2 2 2
𝐸𝑘 = 2 (𝜌1𝑒𝑘 + 𝜌2𝜂𝑘 + 𝜆𝛿𝑘 + 𝜎1𝑟𝑘 + 𝜎2𝑧𝑘 + 𝜎3𝑞𝑘 ), (3.70)
Trong đó
𝑧𝑘(𝑡) = ∫ 𝜂𝑘(𝑡)𝑑𝑡, (3.71)
𝑞𝑘 = 𝜂̇𝑘, (3.72)
and 1, 2, 3 cũng lần lượt là các hệ số dương. Tương tự trong [3], có thể viết:
𝜕𝐸𝑘
= 𝜕𝐸𝑘 − 𝜕𝐸𝑘 + 2 𝜕𝐸𝑘 𝜕𝑟𝑘 − 𝜕𝐸𝑘 𝜕𝜂𝑘 + 𝜕𝐸𝑘 𝜕𝑧𝑘 − 𝜕𝐸𝑘 𝜕𝑞𝑘. (3.73)
𝜕𝜓𝑘
𝜕𝜓𝑘
𝜕𝛿𝑘
𝜕𝑟𝑘 𝜕𝛿𝑘
𝜕𝜂𝑘 𝜕𝛿𝑘
𝜕𝑧𝑘 𝜕𝛿𝑘
𝜕𝑞𝑘 𝜕𝛿𝑘
Thay thế 𝜕𝑟𝑘/𝜕𝛿𝑘 và 𝜕𝜂𝑘/𝜕𝛿𝑘 lần lượt bằng 𝑠𝑖𝑔𝑛(𝜕𝑟𝑘/𝜕𝛿𝑘) = −1 and 𝑠𝑖𝑔𝑛(𝜕𝜂𝑘/𝜕𝛿𝑘) = −1; và để ý rằng có thể thay 𝜕𝑧𝑘/𝜕𝛿𝑘 và 𝜕𝑞𝑘/𝜕𝛿𝑘 bằng các giá trị 𝑠𝑖𝑔𝑛(𝜕𝑧𝑘/𝜕𝛿𝑘) = 1 và 𝑠𝑖𝑔𝑛(𝜕𝑞𝑘/𝜕𝛿𝑘) = −1, thu được:
𝜕𝐸𝑘
𝜕𝜓𝑘
= −𝜌1(𝜓𝑑 − 𝜓𝑘
) − 𝜌2(𝜂𝑑 − 𝜂𝑘
𝜕𝜂𝑘
𝑘
)𝑠𝑖𝑔𝑛(𝜕𝛿 )
−𝜆𝛿
+ 2𝜎 𝑟
𝑠𝑖𝑔𝑛(𝜕𝑟𝑘 ) + 𝜎 𝑧
𝑘
𝑘
𝑠𝑖𝑔𝑛(𝜕𝑧𝑘 ) + 𝜎 𝑞
𝑠𝑖𝑔𝑛(𝜕𝑞𝑘) ,
𝑘 1 𝑘
𝜕𝛿𝑘
2 𝑘
𝜕𝛿𝑘
3 𝑘
𝜕𝛿𝑘
(3.74)
𝜕𝐸𝑘
𝜕𝜓𝑘
= −[𝜌1(𝜓𝑑 − 𝜓𝑘
) − 𝜌2(𝜂𝑑 − 𝜂𝑘) + 𝜆𝛿𝑘
𝑘
𝑘
+𝜎1𝑟𝑘 − 𝜎2𝑧𝑘 + 𝜎3𝑞𝑘] . (3.75)
Khi thay 𝑒𝑘 = 𝜓𝑑 − 𝜓𝑘, 𝜂𝑑 = 0 vào (3.75) sẽ được:
𝑘 𝑘
𝜕𝐸𝑘
𝜕𝜓𝑘
= −[𝜌1
𝑒𝑘
+ 𝜌2
𝜂𝑘
+ 𝜆𝛿𝑘
+ 𝜎1
𝑟𝑘
− 𝜎2
𝑧𝑘
+ 𝜎3
𝑞𝑘
]. (3.76)
Sử dụng luật thích nghi cho mạng nơ-ron như trong [3] sẽ được:
𝑤̇𝑗𝑝 = 𝑂𝑝[𝜑𝑗𝜎(−𝐼𝑗) + 𝛾. 0] = 𝑂𝑝𝜑𝑗𝜎(−𝐼𝑗), (3.77)
𝑤 = −𝛾. 𝜎(𝐼 ). 𝜕𝐸𝑘 , (3.78)
ở đó,
𝑖𝑗
𝑗 𝜕𝜓𝑘
𝜑𝑗 = 𝑤𝑖𝑗 . 𝑤̇ 𝑖𝑗, (3.79)
𝜎(𝐼 ) = 1
, (3.80)
𝑗 1+𝑒𝑥𝑝(−𝐼𝑗)
𝐼𝑗 = ∑𝑝(𝑤𝑗𝑝𝑂𝑝) + 𝜃𝑗. (3.81) Thay (3.76) vào (3.78) sẽ được
𝑤̇ 𝑖𝑗 = 𝛾. 𝜎(𝐼𝑗). (𝜌1. 𝑒𝑘 + 𝜌2𝜂𝑘 + 𝜆𝛿𝑘 + 𝜎1𝑟𝑘 − 𝜎2𝑧𝑘 + 𝜎3𝑞𝑘)
= 𝛾. 𝑂𝑗. (𝜌1. 𝑒𝑘 + 𝜌2𝜂𝑘 + 𝜆𝛿𝑘 + 𝜎1𝑟𝑘 − 𝜎2𝑧𝑘 + 𝜎3𝑞𝑘) . (3.81)
Tóm lại, bộ điều khiển nơ-ron cho AUV có luật cập nhật trọng số mạng nơ-ron cho lớp ẩn và lớp ra lần lượt theo phương trình (3.79) và (3.81). Đây là luật điều khiển thích nghi với độ lệch vị trí AUV do dòng chảy gây ra.
3.6 Kết luận chương 3
Trong Chương 3, tác giả đã trình bày chi tiết mô hình toán học NPS AUV II được sử dụng trong các tình huống mô phỏng. Chương này cũng trình bày nguyên lý BĐK nơ-ron ứng dụng cho AUV mà tác giả đề xuất theo phương án điều khiển riêng biệt (decoupled control) cho các chuyển động của AUV. Các nguyên lý lý thuyết thiết kế BĐK nơ-ron cho hướng đi, độ sâu, tốc độ và toàn bộ chuyển động của AUV được trình bày. Tác giả cũng đề xuất hệ thống điều khiển AUV theo quỹ đạo và bám theo đáy biển. Các phương trình toán học bộ điều khiển, hệ thống dẫn đường trong chương này là cơ sở lập trình mô phỏng và lập trình điều khiển của toàn bộ luận án.
Trong Chương 4 tác giả trình bày kết quả các thí nghiệm mô phỏng trên máy tính cho các thuật toán điều khiển được đề xuất ở Chương 3 và phân tích các kết quả thu được.
CHƯƠNG 4
MÔ PHỎNG ĐIỀU KHIỂN AUV BẰNG BỘ ĐIỀU KHIỂN NƠ-RON THÍCH NGHI
4.1 Giới thiệu phương pháp và điều kiện mô phỏng
4.1.1 Phương pháp mô phỏng
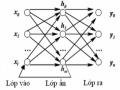
Theo nguyên lý và kết quả trong [3], [8], [9] cấu trúc BĐK nơ-ron dùng cho mô phỏng điều khiển là mạng 3 lớp truyền thẳng. Số lượng nơ-ron lớp vào, lớp ẩn và lớp ra lần lượt là 4, 6 và 1. Phương pháp huấn luyện mạng trực tuyến được áp dụng với số lần huấn luyện trong một chu trình là 50. Thuật toán điều khiển và mạng nơ-ron được viết bằng Matlab M-file.
Dữ liệu mô phỏng và kết quả được tạo và lưu dạng file *.dat để xử lý, phân tích.
4.1.2 Điều kiện mô phỏng
Bảng 4. 1 Các hệ số của mô hình động học NPS AUV II (Matlab code)
= | 7.0e-3; | Xqq | = | -1.5e-2; | Xrr | = | 4.0e-3; | Xpr | = | 7.5e-4; | |
Xudot | = | -7.6e-3; | Xwq | = | -2.0e-1; | Xvp | = | -3.0e-3; | Xvr | = | 2.0e-2; |
Xqds | = | 2.5e-2; | Xqdb2 | = | -1.3e-3; | Xrdr | = | -1.0e-3; | Xvv | = | 5.3e-2; |
Xww | = | 1.7e-1; | Xvdr | = | 1.7e-3; | Xwds | = | 4.6e-2; | Xwdb2 | = | 0.5e-2; |
Xdsds | = | -1.0e-2; | Xdbdb2 | = | -4.0e-3; | Xdrdr | = | -1.0e-2; | Xqdsn | = | 2.0e-3; |
Xwdsn | = | 3.5e-3; | Xdsdsn | = | -1.6e-3; | ||||||
Ypdot | = | 1.2e-4; | Yrdot | = | 1.2e-3; | Ypq | = | 4.0e-3; | Yqr | = | -6.5e-3; |
Yvdot | = | -5.5e-2; | Yp | = | 3.0e-3; | Yr | = | 3.0e-2; | Yvq | = | 2.4e-2; |
Ywp Ydr | = = | 2.3e-1; 2.7e-2; | Ywr | = | -1.9e-2; | Y v | = | -1.0e-1; | Yvw | = | 6.8e-2; |
Zqdot | = | -6.8e-3; | Zpp | = | 1.3e-4; | Zpr | = | 6.7e-3; | Zrr | = | -7.4e-3; |
Zwdot | = | -2.4e-1; | Zq | = | -1.4e-1; | Zvp | = | -4.8e-2; | Zvr | = | 4.5e-2; |
Zw | = | -3.0e-1; | Zvv | = | -6.8e-2; | Zds | = | -7.3e-2; | Zdb2 | = | -1.3e-2; |
Zqn | = | -2.9e-3; | Zwn | = | -5.1e-3; | Zdsn | = | -1.0e-2; | |||
Kpdot | = | -1.0e-3; | Krdot | = | -3.4e-5; | Kpq | = | -6.9e-5; | Kqr | = | 1.7e-2; |
Kvdot | = | 1.2e-4; | Kp | = | -1.1e-2; | Kr | = | -8.4e-4; | Kvq | = | -5.1e-3; |
Kwp | = | -1.3e-4; | Kwr | = | 1.4e-2; | Kv | = | 3.1e-3; | Kvw | = | -1.9e-1; |
Kdb2 | = | 0; | Kpn | = | -5.7e-4; | Kprop | = | 0; | |||
Mqdot | = | -1.7e-2; | Mpp | = | 5.3e-5; | Mpr | = | 5.0e-3; | Mrr | = | 2.9e-3; |
Mwdot | = | -6.8e-3; | Muq | = | -6.8e-2; | Mvp | = | 1.2e-3; | Mvr | = | 1.7e-2; |
Muw | = | 1.0e-1; | Mvv | = | -2.6e-2; | Mds | = | -4.1e-2; | Mdb2 | = | 3.5e-3; |
Mqn | = | -1.6e-3; | Mwn | = | -2.9e-3; | Mdsn | = | -5.2e-3; | |||
Npdot | = | -3.4e-5; | Nrdot | = | -3.4e-3; | Npq | = | -2.1e-2; | Nqr | = | 2.7e-3; |
Nvdot | = | 1.2e-3; | Np | = | -8.4e-4; | Nr | = | -1.6e-2; | Nvq | = | -1.0e-2; |
Nwp | = | -1.7e-2; | Nwr | = | 7.4e-3; | Nv | = | -7.4e-3; | Nvw | = | -2.7e-2; |
Có thể bạn quan tâm!
-
 Điều Khiển Tự Động Dùng Mạng Nơ-Ron Nhân Tạo
Điều Khiển Tự Động Dùng Mạng Nơ-Ron Nhân Tạo -
 Wij O J I , (3.29)
Wij O J I , (3.29) -
 Mô Hình Tổng Quát Của Bộ Điều Khiển Nnc Huấn Luyện Trực Tuyến
Mô Hình Tổng Quát Của Bộ Điều Khiển Nnc Huấn Luyện Trực Tuyến -
 Đáp Ứng Hướng Đi Của Auv Khi Có Dòng Chảy (Tn3)
Đáp Ứng Hướng Đi Của Auv Khi Có Dòng Chảy (Tn3) -
 Đáp Ứng Hướng Đi Của Auv Khi Có Dòng Chảy (Tn5)
Đáp Ứng Hướng Đi Của Auv Khi Có Dòng Chảy (Tn5) -
 Đáp Ứng Độ Sâu Của Auv Trong Tn7
Đáp Ứng Độ Sâu Của Auv Trong Tn7
Xem toàn bộ 169 trang tài liệu này.
Ndr = -1.3e-2; Nprop = 0;
Mô hình toán học NPS AUV II viết trên Matlab M-file được Fossen giới thiệu trong [31], chi tiết trong Phụ lục, các thông số chính liệt kê trong Bảng 4.1. Sơ đồ các tình huống mô phỏng chính được thể hiện trên hình 4.1, hình 4.4 và hình 4.11. Giả thiết về tình huống mô phỏng được nêu trong phần đầu mỗi thí nghiệm mô phỏng.
4.2 Mô phỏng điều khiển các chuyển động của AUV
Các tình huống mô phỏng được thiết lập trên Matlab M-file gồm chương trình chính và nhiều mô-đun có chức năng khác nhau. Tình huống trong phần này gồm các mô-đun sau:
submarine.m: là file chương trình mô phỏng chính.
npsauv.m: là file mô hình toán học AUV.
CurrGen.m: là file tạo ra tác động của dòng chảy lên AUV.
annaiTrain.m: là file chương trình huấn luyện mạng nơ-ron điều khiển theo thuật toán thích nghi tương tác.
mlnnc.m: là file mạng nơ-ron tạo ra các tham số điều khiển.
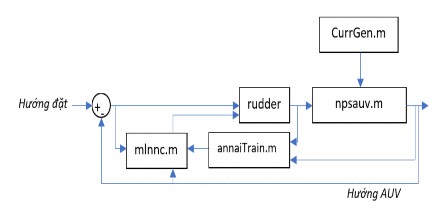
Hình 4.1 Sơ đồ mô phỏng điều khiển hướng AUV
Phần này chỉ mới sử dụng bánh lái hướng và cánh điều khiển độ sâu phía sau của NPS AUV II. Các thí nghiệm mô phỏng được thực hiện trong phần này bao gồm:
- Thí nghiệm 1: Mô phỏng điều khiển riêng hướng đi AUV và so sánh với BĐK PID đơn giản.
- Thí nghiệm 2: Mô phỏng điều khiển độ sâu AUV.