Nâng Cao Hiệu Quả Mô Phỏng Đối Tượng Dạng Sợi, Mảnh

Trong đó:

+ Số điểm điều khiển của NURBS là n+1

+ P(i) là các điểm điều khiển

+ w(i) là trọng số tương ứng với mỗi P(i) và có tác động làm cho NURBS thay đổi có tỷ lệ.

+ N(i,k_u)(u) là hàm cơ sở B-Spline theo miền u với bậc k_u. Hàm N(i,k_u)(u) được biểu diễn bởi công thức (2.7).

- Mô hình NURBS tổng quát được sử dụng để biểu diễn đối tượng có hình dạng mảnh (mặt cong) được xác định bởi công thức sau đây [1,2]:

n

m

w( i , j ) N( i ,k _ u )( u )N( j ,k _ v )( v )P( i , j )

P i 0 j 0

(2.6)

( u ,v )

Trong đó:

n



i 0

m

w( i , j ) N( i ,k _ u )( u )N( j ,k _ v )( v )

j 0

+ Số điểm điều khiển của mô hình NURBS là (n+1)(m+1).

+ P(i,j) là các điểm điều khiển

+ w(i,j) là trọng số tương ứng với mỗi P(i,j) và có tác động làm cho NURBS thay đổi có tỷ lệ.

+ k_u, k_v là bậc của các hàm cơ sở theo hai miền u, v tương ứng.

+ N(i,k_u)(u), N(j,k_v)(v) là các hàm cơ sở B-Spline tương ứng với hai miền u, v.

* Công thức biểu diễn hàm cơ sở N(i,k_u)(u) ứng với chỉ số i và bậc k_u:

N( i ,1 )

( u ) 1 : knotiu knoti1



0 : u [ knoti, knoti1 )

N ( u ) 

u knoti N

( u ) 

knotik _ u u N

( u ) (2.7)

( i ,k _ u )

Trong đó:

knotik _ u1

knoti

( i ,k _ u1 )

knotik _ u

knoti1

( i1,k _ u1 )

+ k_u là bậc của hàm cơ sở B-Spline theo miền u.

+ knoti là các vectơ nút, gồm tập hợp các phần tử kiểm soát độ cong của sợi và mảnh.

* Công thức biểu diễn hàm cơ sở N(j,k_v)(v) ứng với chỉ số j và bậc k_v:

N( j ,1)

(v) 1: knotjv knotj1



0 : v [knotj , knotj1 )

N (v) 

v knotj N

(v) 

knotjk _ v v N

(v)

(2.8)

( j,k _ v)

knot

jk _ v1

knotj

( j,k _ v1)

knot

jk _ v

knot

j1

( j1,k _ v1)

Trong đó:

+ k_v là bậc của hàm cơ sở B-Spline theo miền v.

+ knotj là các vectơ nút, gồm tập hợp các phần tử kiểm soát độ cong của sợi và mảnh.

- Các vectơ nút knoti, knotj là những tập hợp các phần tử kiểm soát độ cong của sợi và mảnh theo các miền tương ứng i và j.

Vectơ nút với miền u và chỉ số i được biểu diễn như sau:

{knot0,knot1,...,knotn+k_u-1,knotn+k_u}

Số phần tử của một vectơ nút được tính bằng tổng (n+k_u+1) Vectơ nút với miền v và chỉ số j được biểu diễn như sau:

{knot0,knot1,...,knotn+k_v-1,knotn+k_v}

Số phần tử của một vectơ nút được tính bằng tổng (n+k_v+1)

Vectơ nút là một tập hợp các phần tử kiểm soát độ cong của sợi và mảnh, thể hiện sợi hay mảnh cong là đều hay không đều, tuần hoàn hay không tuần hoàn,…

Dựa vào đặc điểm của mô hình NURBS được đưa ra để mô hình hoá và điều khiển mô hình các đối tượng có hình dạng sợi hay mảnh cong với độ cong lồi lõm bất kỳ, cục bộ, tức là không đều, không tuần hoàn nhưng chúng vẫn có độ trơn cần thiết như mô hình các sợi tóc, vải,...

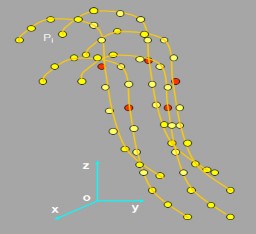
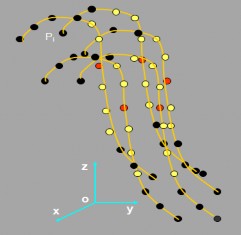
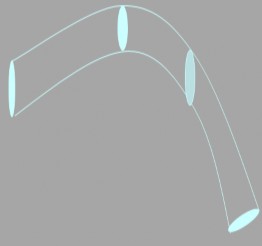
Hình dưới đây minh họa việc mô phỏng một số đối tượng có hình dạng sợi, mảnh dựa vào mô hình NURBS.

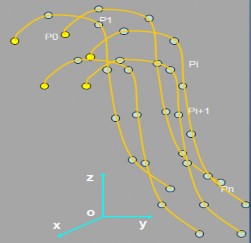
Hình 2.10. Mô phỏng đối tượng dạng sợi

Hình 2.11. Mô phỏng đối tượng dạng mảnh

2.2.2. Nâng cao hiệu quả mô phỏng đối tượng dạng sợi, mảnh

Một trong những vấn đề luôn được đặt ra trong các bài toán mô phỏng, đó là vấn đề về tốc độ. Vì dữ liệu trong quá trình mô hình hóa các đối tượng trong các bài toán mô phỏng thường lớn, hơn nữa các đối tượng dạng sợi, mảnh thường có tính cục bộ như tóc, vải. Dựa vào đặc điểm, khi các đối tượng dạng sợi hay mảnh như vải, tóc chuyển động hay bị tác động thì luôn có những bộ phận gần như không bị ảnh hưởng, ít có sự dịch chuyển. Trong phần này, bài báo đề xuất kỹ thuật nâng cao hiệu quả mô phỏng các đối tượng dạng sợi, mảnh dựa vào mô hình NURBS, trên cơ sở hiệu chỉnh giảm miền ảnh hưởng của các điểm điều khiển tác động lên điểm đang xét nhằm tăng tốc độ mô phỏng, tăng tính cục bộ của đối tượng.

Do mô hình NURBS được sử dụng để mô phỏng đối tượng dạng sợi theo công thức (2.8) và mảnh theo công thức (2.9), mà trong chúng đều có hàm cơ sở B- Spline, một đại lượng chính ảnh hưởng lớn tới giá trị của NURBS và được biểu diễn theo công thức (2.7) theo miền u và chỉ số i, miền v và chỉ số j trong mục 2.2.2 ở trên.

Do các hàm cơ sở N(i,k_u)(u), N(j,k_v)(v) được biểu diễn bởi các công thức giống nhau và chỉ khác nhau về các miền và chỉ số. Nên để thuận tiện cho quá trình trình bày, bài báo chỉ trình bày đề xuất cải tiến dựa vào hàm cơ sở N(i,k_u)(u) ứng với miền u và chỉ số i, còn đề xuất dựa vào với hàm cơ sở N(j,k_v)(v) được trình bày tương tự.

Công thức biểu diễn hàm cơ sở N(i,k_u)(u):

N( i ,1 )

( u ) 1 : knoti u knoti 1



0 : u [ knoti , knoti 1 )

N ( u ) 

u knoti N

( u ) 

knoti k _ u u N

( u )

( i ,k _ u )

knoti k _ u 1

knoti

( i ,k _ u 1 )

knoti k _ u

knoti 1

( i 1,k _ u 1 )

Theo công thức trên, với một vectơ nút không giảm và nằm trong đoạn [0,1] thì giá trị của hàm cơ sở N(i,k_u)(u) sẽ giảm dần theo khoảng cách giữa điểm đang xét với một điểm điều khiển bất kỳ và giá trị của hàm cơ sở N(i,k_u)(u) thể hiện sự ảnh hưởng của điểm điều khiển P(i) tới điểm đang xét P(u). Tức là, sự ảnh hưởng của các điểm điều khiển càng xa điểm đang xét thì sự ảnh hưởng của nó càng nhỏ, knoti là giá trị tại nút P(u) với biến số là u được gọi là vectơ nút.

Trong trường hợp phù hợp, với giá trị của một vectơ nút và bậc của hàm cơ sở N(i,k_u)(u) là k_u thì sẽ có 2k_u giá trị của hàm cơ sở N(i,k_u)(u)≠0 nằm đều về hai bên của điểm đang xét, còn lại các giá trị khác đều bằng không. Vấn đề đặt ra là xây dựng vectơ nút như thế nào để thỏa mãn được tính chất trên.

Trong thực tế, khi mô phỏng các đối tượng 3D dạng sợi hay mảnh, không phải vị trí nào của đối tượng cũng cần trơn, hay cong đều mà có những vị trí trơn nhưng lại có những độ cong bất kỳ, cục bộ (hình 1, 2). Với những vị trí đối tượng có độ cong, lồi lõm cục bộ như hình 1,2 ở trên thì đòi hỏi khi thay đổi vị trí của một điểm điều khiển thì yêu cầu phải có sự thay đổi cục bộ chứ không phải toàn cục trên

đối tượng. Để đáp ứng yêu cầu trên, người ta đưa ra một kiểu vectơ nút không đều ở trên.

Tuy nhiên, từ công thức mô phỏng đối tượng dạng sợi (2.8) và mảnh (2.9), có thể thấy với mỗi điểm đang xét, nó được tính toán từ tập tất cả các điểm điều khiển, trong khi các đối tượng lại có tính chất cục bộ [61,62,65]. Như vậy, dẫn tới tốc độ mô phỏng chậm. Vấn đề đặt ra là: làm thế nào để có thể thu nhỏ miền ảnh hưởng của các điểm điều khiển lên điểm đang xét, làm cho tính chất cục bộ của đối tượng được thể hiện rõ ràng hơn và tăng tốc độ mô phỏng mà không làm ảnh hưởng nhiều tới chất lượng của mô hình?

Hình 2.12 minh họa cho trường hợp phù hợp, với A là điểm đang xét có u=4, bậc k_u=2 thì điểm nằm trong miền 2u6 là các điểm điều khiển tác động lên điểm A mà có N(i,k_u)(u)0, còn lại các điểm khác đều có N(i,k_u)(u)=0, tức là không ảnh hưởng lên điểm A.

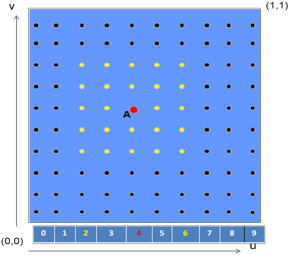
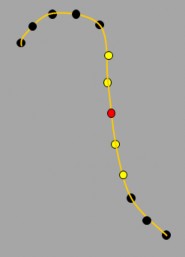
Hình 2.12. Xác định vectơ nút ứng với trường hợp tối ưu

Trong thực tế, việc mô hình hoá và mô phỏng các đối tượng 3D dạng sợi hay mảnh không đều, lồi lõm cục bộ là rất cần thiết mà dùng mô hình NURBS tổng quát thì khó có thể đáp ứng được cả về 2 mặt chất lượng cũng như tốc độ.

Trên cơ sở các phân tích ở trên, nhằm tăng tốc độ mô phỏng, bài báo này đề xuất hiệu chỉnh giảm miền ảnh hưởng của các điểm điều khiển lên điểm đang xét do các đối tượng dạng sợi hay mảnh như vải, tóc,... thường có tính chất cục bộ, nên

việc ảnh hưởng của chúng chỉ xảy ra có tính chất cục bộ chứ không xảy ra trên toàn bộ đối tượng. Việc giảm ảnh hưởng này trên cơ sở xây dựng các vectơ nút.

Với vectơ nút đều tuần hoàn hoặc không đều thì tại một nút đang xét, nút đó sẽ chịu sự ảnh hưởng của toàn bộ các điểm điều khiển, tức là N(i,k_u)(u)≠0 với mọi i. Với vectơ nút là không tuần hoàn, thì giá trị của N(i,k_u)(u)≠0 khi và chỉ khi (nowu-k_u)i(nowu+k_u), trong đó nowu là giá trị thứ tự của điểm đang xét A. Trong hình 2.12 ở trên, với k_u=2, nowu=4 thì 2i6.

Qua thực nghiệm, ta xác định được công thức tính vectơ nút knoti với miền u, bậc hàm cơ sở k_u và chỉ số i sau:



knot 

0

k _ u 1 ) /( n k _ u 1 )

0 i k _ u

k _ u i n



i ( i

1

n i n k _ u

(2.9)

Còn công thức tính vectơ nút knotj với miền v, bậc hàm cơ sở k_v và chỉ số j sẽ được trình bày tương tự và chỉ việc thay i=j, k_u=k_v và n=m và như vậy, ta xác định được công thức tính vectơ nút knotj như sau:

 0 0 j k _ v

knotj





( j

k _ v  1) /(n k _ v  1)

k _ v 

j n

(2.10)

1



n 

j n k _ v

* Công thức mô hình NURBS cải tiến trong mô phỏng các đối tượng dạng sợi và mảnh được viết như sau:

- Công thức NURBS mô phỏng đối tượng dạng sợi (2.8) trở thành (2.11):

nowu k _ u

N( i ,k _ u ) ( u )w( i ) P( i )



P( u )

i nowu k _ u

nowu k _ u

N( i ,k _ u ) ( u )w( i ) i nowu k _ u

(2.11)

- Công thức NURBS mô phỏng đối tượng mảnh (2.9) trở thành (2.12):

nowu k _ u



nowvk _ v

w( i , j ) N( i ,k _ u ) ( u )N( j ,k _ v ) ( v )P( i , j )

P i nowu k _ u j nowvk _ v

( u ,v )

nowu k _ u



nowvk _ v

w( i , j ) N( i ,k _ u ) ( u )N( j ,k _ v ) ( v )

(2.12)

i nowu k _ u j nowvk _ v

Trong đó: nowu và nowv là các giá trị thứ tự của điểm đang xét theo hai miền u và v tương ứng.

Với công thức cải tiến NURBS trong mô phỏng đối tượng dạng sợi (2.11) và mảnh (2.12), khi thay đổi vị trí của một điểm điều khiển thì chỉ ảnh hưởng tới 2k_u điểm khác. Hơn nữa, nó lại đáp ứng được yêu cầu chỉ thay đổi cục bộ các điểm đang xét trên mô hình đối tượng và có thể đáp ứng mô phỏng những vị trí của đối tượng có độ cong mong muốn, kể cả những vị trí có độ cong phức tạp. Hình

2.13 1 minh họa các miền ảnh hưởng của các điểm điều khiển lên một điểm đang xét giữa mô hình NURBS ở công thức (2.8) và (2.11).

NURBS ở công thức (2.8)	NURBS ở công thức (2.11)

Có thể bạn quan tâm!

• Từ Trái Sang Phải Là Các Thao Tác Dịch Chuyển, Xoay, Co Giãn, Ứng Với Mỗi Trục Toạ Độ Là Một Màu.
• Kỹ Thuật Mô Phỏng Đối Tượng Dạng Ảnh Dựa Vào Texture Mapping
• Nội Suy Các Điểm Còn Lại Để Đảm Bảo Ràng Buộc Trong Một Vùng Tóc
• Kỹ Thuật Mô Phỏng Đối Tượng Dựa Vào Mass-Springs
• Kết Quả Thử Nghiệm Kỹ Thuật Mô Phỏng Sử Dụng Nurbs
• Kỹ thuật mô phỏng đối tượng dạng sợi và ứng dụng mô phỏng tóc trong thực tại ảo - 9

Xem toàn bộ 81 trang tài liệu này.

Hình 2.13. Miền ảnh hưởng của các điểm điều khiển lên điểm đang xét

* Đánh giá độ phức tạp:

- Mô phỏng đối tượng dạng sợi: So sánh độ phức tạp giữa công thức (2.8) và (2.11) ta thấy, từ công thức (2.8) ta tính được độ phức tạp của thuật toán này như sau: Giả sử O(l) là độ phức tạp của hàm cơ sở B-Spline theo u.

Khi đó, độ phức tạp tính toán của một điểm trên mô hình đối tượng được biểu diễn bởi công thức (2.8) là: O(n*l), trong khi độ phức tạp tính toán của một điểm trên mô hình đối tượng được biểu diễn bởi công thức (2.11) là: O(k_u*l).

Khi đó, O(k_u*l)<O(n*l) vì k_un.

- Mô phỏng đối tượng dạng mảnh: So sánh độ phức tạp giữa công thức (2.9) và (2.12) ta thấy, từ công thức (2.9) ta tính được độ phức tạp của thuật toán này như sau:

Giả sử O(p+q) là độ phức tạp của hàm cơ sở B-Spline, khi đó độ phức tạp tính toán của một điểm trên mô hình đối tượng được biểu diễn bởi NURBS ở công thức (2.9) là: O(m*n*(p+q)). Trong khi đó, độ phức tạp tính toán của một điểm trên được biểu diễn bởi công thức (2.12) là: O(k_u*k_v*(p+q)).

Khi đó, O(k_u*k_v*(p+q))<O(m*n*(p+q)) vì k_un, k_vm.

2.2.3. Thuật toán mô phỏng đối tượng dạng sợi AHS

Thuật toán AHS (Attaching Hairs to Scalp) mô phỏng theo mô hình NURBS cải tiến trên mô hình C, gồm các bước sau: Đầu tiên là xây dựng tập vectơ hướng P cho mỗi sợi ứng với mỗi điểm P trên C. Tiếp theo là phủ sợi lên C: với mỗi điểm PC, xây dựng sợi tại vị trí P với m điểm điều khiển Tq, vectơ hướng P với điểm điều khiển đầu tiên là: T1=P, các điểm điều khiển tiếp theo của sợi được tínhP *leng. Cuối cùng, hiển thị sợi kết quả.

* Thuật toán mô phỏng sợi AHS:

Đầu vào: Bề mặt mô hình C,

n số sợi, m điểm điều khiển Tq|q=1,..,m trên mỗi sợi, độ dài đoạn sợi leng,

Tổng hợp ngoại lực tác động vào mỗi điểm điều khiển ={wind}{gravity}, wind là ngoại lực tác động của gió thổi,gravity là ngoại lực tác động của trọng lực.