94
Đối với những nội dung có nhiệm vụ hướng dẫn HS giải bài tập.
Lời giải cho một bài toán có thể chiếm nhiều trang màn hình. Để giúp HS được lần lượt tiếp cận với các nội dung chi tiết của lời giải, chúng tôi đã vận dụng lý thuyết về các bước giải bài tập của Polia để phân chia lời giải thành các trang, trong đó mỗi trang lại có thể tích hợp các đường link chuyển đến các trang khác và các nội dung lý thuyết làm cơ sở cho mỗi bước giải như sau:
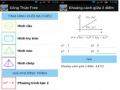
Trang 1 bao gồm những thông tin
giúp HS xác định rõ bài toán và hiểu được
Hình 2.16
những yếu tố chưa tường minh ẩn chứa trong lời phát biểu của bài toán.
Trang 2 bao gồm những thông tin có tính chất gợi mở, dẫn dắt HS phát hiện ra hướng giải quyết bài toán.
Trang 3 trình bày lời giải của bài toán.
Trang 4 trình bày một số bài toán tương tự (để HS rèn luyện kỹ năng giải toán) hoặc những câu hỏi đặt ra từ lời giải bài toán để HS tìm tòi, phát triển mở rộng bài toán hoặc đưa ra thêm những hướng giải quyết mới cho bài toán.
2.4. Quy trình khai thác một số ứng dụng trên điện thoại di động hỗ trợ học sinh tự học Toán
Như đã trình bày ở chương 1, ở Việt Nam hiện nay đã có một số hệ thống M-learning hỗ trợ HS tự học Toán. Như vậy, GV hoàn toàn có thể giới thiệu với HS các hệ thống M-learning này tương tự như những biện pháp mà đề tài đã triển khai đối với hệ thống M-learning do đề tài thiết kế, biên tập nguồn HLĐT.
95
Qua nghiên cứu lý luận và tìm hiểu thực tiễn, việc khai thác một số ứng dụng trên ĐTDĐ hỗ trợ HS tự học Toán được chúng tôi xác định và triển khai theo các bước sau:
Bước 1: Xác định mục tiêu, nhiệm vụ tự học
Để triển khai tự học, trước hết GV phải xác định mục tiêu tự học mà ta hướng tới. Tiếp theo, căn cứ vào mục tiêu, GV định hướng cho từng nhóm HS, từng HS xác định nhiệm vụ tự học một cách cụ thể (qua phiếu học tập hoặc trên trang web).
Ví dụ sau khi học xong bài “Phương trình mặt phẳng” [26], mục tiêu, nhiệm vụ tự học của HS được xác định như sau:
Mục tiêu:
Hiểu được bản chất các khái niệm, công thức trong bài học ”Phương trình mặt phẳng” và vận dụng chúng vào giải bài tập.
Nhiệm vụ của HS:
(i). Căn cứ vào bài giảng (kết hợp trí nhớ với vở ghi, SGK) và tóm tắt những kiến thức cơ bản cần nhớ vào vở (*).
(ii). Sử dụng ĐTDĐ để truy cập mục “Phương trình mặt phẳng trong không gian” tại địa chỉ: http://mlearningvn.com đọc nội dung “Tóm tắt kiến thức cần nhớ” và so sánh với (*) và tiếp tục bổ sung để hoàn thiện hệ thống các kiến thức trọng tâm của bài.
(iii). Trong quá trình tự học nếu có khó khăn hoặc sau khi hoàn thành nhiệm vụ thì thông báo kết quả lên hệ thống.
Bước 2: Xác định nội dung thông tin
Nhiệm vụ của GV trong bước này là phải xác định những tri thức, kỹ năng tối thiểu, nguồn thông tin tham khảo mà HS cần biết để hoàn thành các nhiệm vụ tự học, đặc biệt là tri thức sự vật và tri thức phương pháp. Một phần các tri thức này sẽ được thể hiện ngay trong nội dung HLĐT do GV chuẩn bị, một phần sẽ gồm các đường link để truy cập đến nguồn thông tin này.
96
Ví dụ, với nhiệm vụ tự học nội dung “Phương trình mặt phẳng”, nội dung thông tin dành cho HS bao gồm các phần: Các bài trắc nghiệm, bài tập, hệ thống lý thuyết... giúp HS phát hiện và giải quyết các vấn đề nảy sinh trong quá trình giải bài tập và các đề trắc nghiệm được chúng tôi thiết kế, biên tập như sau:
![]()
![]()
![]()
![]()
![]()
![]()
(a) Bài tập trắc nghiệm:
Kịch bản và thông tin trợ giúp | |
Bài tập 1: Mặt phẳng (P) qua A(1; 4; -3) và song song với mặt phẳng (Q): 2x – 4y + 3z – 2 = 0 có phương trình: A. 2x – 4y + 3z – 23 = 0 B. 2x + 4y + 3z – 10 = 0 C. 2x – 4y + 3z + 23 = 0 D. 2x – 4y + 3z – 10 = 0 | - Nếu HS chọn đáp án khác C, hệ thống hiện thông báo đã sai yêu cầu HS chọn lại. - Nếu HS nhấp chuột vào mục trợ giúp, sẽ nhận được thông tin: “Vì mp(P) song song với mp(Q): 2x – 4y + 3z – 2 = 0 nên (P) có dạng: 2x – 4y + 3z + D = 0 Vì mp(P) qua A(1;4;-3) tọa độ điểm D thỏa mãn phương trình mặt phẳng”. Với sự trợ giúp trên, HS sẽ thay số để có: 2.1 – 4.4 +3.(-3) + D = 0, từ đó tính được D và viết được phương trình mặt phẳng (P). - Nếu HS đã chọn được đáp án đúng, hệ thống tiếp tục đưa ra yêu cầu tiếp theo: |
Bài 2: Mặt phẳng (P) đi qua hai điểm A(1;0;1), B(2;1;2) và vuông góc với mặt phẳng (Q): x + 2y + 3z – 2010 = 0 có phương trình: A. x – 2y + z = 0 B. x + 2y + 3z – 4 = 0 C. x – 2y + z + 2 = 0 D. x – 2y + z – 2 = 0 | -Nếu HS chọn sai đáp án sẽ nhận được sự trợ giúp: “Ta có, AB 1;1;1, nQ 1; 2;3nên véc tơ pháp tuyến của mp(P) là nP AB nQ . Như vậy cần tính được nP để từ đó viết được phương trình mặt phẳng (P) qua A(1;0;1) có véctơ pháp tuyến là nP ” |
Có thể bạn quan tâm!
-
 Quy Trình Xây Dựng Hệ Thống M-Learning Hỗ Trợ Học Sinh Lớp 12 Tự Học Toán
Quy Trình Xây Dựng Hệ Thống M-Learning Hỗ Trợ Học Sinh Lớp 12 Tự Học Toán -
 Minh Họa Mô Hình Các Mô Đun Của Hệ Thống M-Learning
Minh Họa Mô Hình Các Mô Đun Của Hệ Thống M-Learning -
 Xây Dựng Học Liệu Điện Tử Hỗ Trợ Học Sinh Tự Học Toán Thông Qua Việc Khai Thác Một Số Ứng Dụng Trên Điện Thoại Di Động
Xây Dựng Học Liệu Điện Tử Hỗ Trợ Học Sinh Tự Học Toán Thông Qua Việc Khai Thác Một Số Ứng Dụng Trên Điện Thoại Di Động -
 Phương Án Tự Học Có Hướng Dẫn Trực Tiếp Của Giáo Viên
Phương Án Tự Học Có Hướng Dẫn Trực Tiếp Của Giáo Viên -
 Phương Án Khai Thác Một Số Ứng Dụng Trên Điện Thoại Di Động Trong Tự Học Toán Của Học Sinh Trong Giờ Lên Lớp Chính Khóa
Phương Án Khai Thác Một Số Ứng Dụng Trên Điện Thoại Di Động Trong Tự Học Toán Của Học Sinh Trong Giờ Lên Lớp Chính Khóa -
 Thời Gian, Địa Điểm Và Đối Tượng Thực Nghiệm Sư Phạm
Thời Gian, Địa Điểm Và Đối Tượng Thực Nghiệm Sư Phạm
Xem toàn bộ 221 trang tài liệu này.

97
![]()
![]()
![]()
![]()
![]()
d(M,() ) | A.x0 By0 Cz0 D |
A2 B2 C2 | |
(b). Bài tập đơn giản vận dụng trực tiếp lý thuyết
Kiến thức bổ trợ (nếu HS kích hoạt yêu cầu trợ giúp) | |
Bài tập 1: Trong không gian Oxyz, viết phương trình tổng quát của mặt phẳng () trong các trường hợp sau: a) () đi qua M (3; 2; -5) và nhận véc tơ n(2; 3;1) làm véc tơ pháp tuyến. b) () là mặt phẳng trung trực của đoạn thẳng AB với A3; 5; 4 , B1 ; 3; 2 | Dạng phương trình tổng quát của phương trình mặt phẳng khi biết véc tơ pháp tuyến và một điểm thuộc mặt phẳng là: A(x x0 ) B(y y0 ) C(z z0 ) 0. a)Hãy thay tọa độ M (3; 2; -5) và tọa độ của véc tơ pháp tuyến n(2; 3;1) vào phương trình tổng quát và rút gọn b) Để làm được ý b), Hãy nhớ lại: - Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng như thế nào? - Cách tìm tọa độ trung điểm như thế nào? - Véc tơ pháp tuyến là véc tơ nào? Và cách tìm chúng bằng công thức nào? |
Bài tập 2: Trong không gian Oxyz, viết phương trình tổng quát của mặt () chứa 3 điểm A(2;0;0), B(0;-3;0), C(0;0;5). | Áp dụng công thức phương trình mặt phẳng theo đoạn chắn x y z 1 cắt các trục Ox, Oy, Oz lần lượt tại các a b c điểm A(a;0;0), B(b;0;0); C(c;0;0). Hãy thay tọa độ 3 điểm A, B,C vào phương trình trên và rút gọn. |
Bài tập 3: Trong không gian Oxyz, viết phương trình mặt phẳng () đi qua M1; 2;3và song song với mặt phẳng () 3x 2y 4z 1 0. | Hai mặt phẳng mà song song với nhau sẽ có cùng véc tơ pháp tuyến. Như vậy mặt phẳng () có véc tơ pháp tuyến là n. Thay vào công thức A(x x0 ) B(y y0 ) C(z z0 ) 0 và rút gọn |
Bài tập 4: Trong không gian Oxyz, viết phương trình mặt phẳng () đi qua hai điểm P(1;- 1;1), Q(2;1;5) và vuông góc với mặt phẳng () x 2y 3z 11 0 . | () đi qua hai điểm P, Q và vuông góc với mặt phẳng () nên nó song song với giá của các véc tơ nvà PQ. Từ đó suy ra véc tơ pháp tuyến của () là n n, PQ. Thay vào công thức A(x x0) B(y y0) C(z z0) 0 sau đó rút gọn |
Bài tập 5: Trong không gian Oxyz, cho điểm M(2;-1;3) và mặt phẳng () x 2y 2z 1 0 a) Tính khoảng cách từ điểm M đến mặt phẳng (). b) Tìm điểm N trên trục Ox sao cho khoảng cách từ N đến()bằng khoảng cách từ M đến (). | a) Áp dụng công thức tính khoảng cách từ điểm M(x0; y0;z0 ) đến (): A.x0 By0 Cz0 D 0 Thay trực tiếp và tính Toán được ngay kết quả. b) Do N thuộc Ox suy ra N(n;0;0), ta có: d(N, () ) 3 . Từ đó ta có phương trình với ẩn n, giải phương trình này ta sẽ suy ra tọa độ điểm N. |
98
Tự kiểm tra: Hãy tự khẳng định lại nhận định của mình bằng cách trả lời các câu hỏi trắc nghiệm số 1 mục “Phương trình mặt phẳng trong không gian” (15 câu – thời gian 20 phút, các câu hỏi được chọn ngẫu nhiên từ ngân hàng câu hỏi của HLĐT).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
d(M,() ) | A.x0 By0 Cz0 D |
A2 B2 C2 | |
(c). Bài tập cơ bản:
Kiến thức bổ trợ (nếu HS kích hoạt yêu cầu trợ giúp) | |
Bài tập 6: Viết phương trình mặt phẳng (P) trong các trường hợp sau. a) (P) đi qua M(2;-3;1) và song song với() x 2y 2z 1 0 b) (P) là mặt phẳng trung trực của đoạn thẳng AB với A(-1;2;- 5), B(5;3;2). | a) Véc tơ pháp tuyến của (P) chính là véc tơ pháp tuyến của () . Sau đó Áp dụng công thức để viết phương trình mặt phẳng. b) Mặt phẳng trung trực của đoạn thẳng AB, là mặt phẳng đi qua trung điểm của AB và vuông góc với AB. Như vậy, các em làm theo các bước sau: + Tìm trung điểm I của đoạn thẳng AB + Tìm véc tơ pháp tuyến AB . + Áp dụng công thức để viết phương trình mặt phẳng. |
Bài tập 7: Viết phương trình mặt phẳng (P) trong các trường hợp sau. a) (P) đi qua ba điểm A(-1;2;1), B(2;3;0), C(1;-1;-2) b) (P) đi qua M(1;0;-1), N(3;-1;2) và vuông góc với () 2x y z 1 0. c) (P) đi qua I(1; 2; 1) và vuông góc với giao tuyến của hai mặt phẳng (Q): x y z 1 0 và (R) : x y z 5 0 | a) Mặt phẳng (P) đã biết điểm đi qua. (Chọn một trong 3 điểm A, B, C). Do mp(P) chứa A, B, C nên có cặp véc tơ chỉ phương là AB , AC , suy ra véc tơ pháp tuyến là: nPAB, AC b) Do mp(P) đi qua M, N nên giá của véc tơ MN song song với (P). Do mp(P) vuông góc với () nên giá của véc tơ pháp tuyến ncủa () song song với mp(P). Từ đó, suy ra mp(P) có cặp véc tơ chỉ phương là MN và n. Véc tơ pháp tuyến của mp(P) là nPMN, n. c) Do mp(P) vuông góc với mp(Q) và mp(R) nên mp(P) có cặp véc tơ chỉ phương là nQ và nR . Suy ra véc tơ pháp tuyến của mp(P) là: nPnQ, nR |
Bài tập 8: Viết phương trình mặt phẳng (P) song song với () 2x y z 1 0 và tiếp xúc với mặt cầu (S) (x 2)2 (y 1)2 (z 1)2 9. | Do mp(P) song song với () nên mp(P) có dạng 2x y z m 0 (m 1) Do mp(P) tiếp xúc với mặt cầu (S) nên khoảng cách từ tâm mặt cầu (S) đến mp(P) bằng bán kính mặt cầu. Áp dụng công thức tính khoảng cách Từ đó, ta tìm được tham số m, sau đó suy ra mặt phẳng cần tìm. |
99
Tự kiểm tra: Hãy tự khẳng định lại nhận định của mình bằng cách trả lời các câu hỏi trắc nghiệm mục “Phương trình mặt phẳng trong không gian” (15 câu – thời gian 20 phút, hệ thống câu hỏi được chọn ngẫu nhiên từ ngân hàng câu hỏi).
(d). Bài tập nâng cao:
Kiến thức bổ trợ (nếu HS kích hoạt yêu cầu trợ giúp) | |
Bài tập 9: Viết phương trình mặt phẳng (P) song song và cách () x y z 3 0 một khoảng bằng 3. | Hãy tìm cách trả lời các câu hỏi sau: - (P) song song với () x y z 3 0 thì (P) có dạng như thế nào? - Khoảng cách giữa (P) và () được hiểu như thế nào, tính chúng bằng công thức nào? - Làm thế nào để chọn điểm M thuộc () - Tính khoảng cách từ điểm M đến mặt phẳng P: d(M, (P) ) bằng công thức nào? Gợi ý: Từ giả thuyết d(M, (P) ) 3giải phương trình với ẩn m. Từ đó, ta tìm ra m và suy ra phương trình mặt phẳng (P). |
Bài tập 10: Trong không gian, cho tứ diện OABC có OA, OB, OC đôi một vuông góc, OA = a, OB = b, OC = c. Tính độ dài đường cao của tứ diện hạ từ đỉnh O. | Bước 1: Chọn hệ trục tọa độ: Do OA, OB, OC đôi một vuông góc, nên ta có thể chọn hệ trục tọa độ sao cho O là gốc tọa độ, OA nằm trên Ox, OB nằm trên Oy, OC nằm trên Oz. Bước 2: Tìm tọa độ của một số điểm liên quan đến bài giải theo hệ trục vừa chọn: Với hệ trục vừa chọn, ta có A(a; 0;0), B(0;b;0), C(0;0;c), O(0;0;0). Bước 3: Giải bài toán bằng phương pháp tọa độ Viết phương trình mặt phẳng (ABC). Độ dài đường cao hạ từ O bằng khoảng cách từ O đến mặt phẳng (ABC). |
Bài tập 11: Cho hình chóp đều S.ABCD, đáy ABCD là hình vuông cạnh a, chiều cao hạ từ đỉnh S của hình chóp bằng b. Tính khoảng cách từ đường thẳng CD đến mặt phẳng (SAB). | Ta có thể chọn hệ trục tọa độ sao cho: Tâm hình vuông ABCD trùng với gốc tọa độ O, AC nằm trên Ox, BD nằm trên Oy và OS nằm trên Oz Khi đó A( a 2 ;0;0), C(- a 2 ;0;0), B(0; a 2 ;0), 2 2 2 D(0;- a 2 ;0), S(0;0;b), O(0;0;0). 2 Chứng minh CD song song với mp(SAB). Khi đó khoảng cách từ đường thẳng CD đến mặt phẳng (SAB) bằng khoảng cách từ C đến mp(SAB). |
100
Hãy tự khẳng định lại nhận định của mình bằng cách trả lời các câu hỏi trắc nghiệm mục “Phương trình mặt phẳng trong không gian” (15 câu – thời gian 20 phút, hệ thống câu hỏi được chọn ngẫu nhiên từ hệ thống câu hỏi, bài tập kèm theo bài giảng).
Bước 3: Tổ chức cho HS tự học
Việc tổ chức cho HS tự học là quá trình thông qua các biện pháp sư phạm với sự hỗ trợ của ĐTDĐ, trên cơ sở nguồn HLĐT đã thiết kế, GV giúp HS chủ động tự giác, triển khai các công đoạn chính sau:
- Hình thành động cơ, xác định nhiệm vụ tự học một cách cụ thể;
- Xây dựng kế hoạch tự học cho bản thân, trong đó xác định rõ những nội dung tri thức, kỹ năng cần chiếm lĩnh và địa chỉ nguồn thông tin;
- Thực hiện kế hoạch tự học, lần lượt thực hiện từng nhiệm vụ đã đề ra trong kế hoạch;
- Kiểm tra đánh giá mức độ hoàn thành nhiệm vụ tự học.
Ví dụ, với mục đích, nhiệm vụ tự học nội dung “Phương trình mặt phẳng” được thiết kế như trên, HS sẽ tự lên kế hoạch và lựa chọn thời gian phù hợp để dành ra khoảng thời gian từ 1 đến 2 giờ tự học qua ĐTDĐ. Nếu gặp khó khăn, trước hết HS sẽ sử dụng các gợi ý có sẵn trên trang web, tiếp theo có thể đưa vấn đề lên diễn đàn để tranh thủ sự hỗ trợ của các bạn và GV.
Bước 4: Đánh giá kết quả tự học của HS.
Việc đánh giá kết quả tự học của HS có thể triển khai với các hình thức quen thuộc vẫn được sử dụng trong dạy học Toán, tuy nhiên điểm khác biệt trong kiểm tra đánh giá kết quả tự học của HS với sự hỗ trợ của ĐTDĐ là:
- Việc đánh giá kết quả tự học xảy ra song song với quá trình tự học của HS, cụ thể: Vừa tự học, HS vừa tự trả lời các câu hỏi trắc nghiệm để tự mình đánh giá và điều chỉnh phương án tự học. Mặt khác, kết quả tự học của mỗi HS sẽ được kiểm định thông qua quá trình trao đổi, tương tác giữa HS với HS trong quá trình tự học.
101
- Việc đánh giá được thực hiện từ nhiều phía vào nhiều thời điểm kể cả việc đánh giá trực tuyến do GV, các HS tham gia tự học và bản thân HS.
Kết quả tự học của HS được đánh giá qua các kênh thông tin sau:
- Trao đổi giữa GV và HS, trao đổi giữa HS với HS trong quá trình HS tự học và trong các giờ học Toán sau đó;
- Kết quả trả lời các câu hỏi trắc nghiệm khách quan đi kèm với ba mức độ của từng HS.
- Kết quả kiểm tra 15 phút, 45 phút, thi học kỳ...
Trong quá trình HS tự học, căn cứ vào mục tiêu tự học, GV có thể tiếp tục giao bổ sung nhiệm vụ tự học cho HS qua phiếu học tập hoặc qua hệ thống theo định hướng phân hóa, nâng cao dần yêu cầu.
2.5. Phương án khai thác một số ứng dụng trên điện thoại di động trong tự học Toán của học sinh ngoài giờ lên lớp
2.5.1. Đối tượng “giáo viên”, “học sinh” tham gia hệ thống
Trong quá trình nghiên cứu, triển khai việc khai thác một số ứng dụng trên ĐTDĐ hỗ trợ HS lớp 12 tự học Toán, hai đối tượng chính tham gia hệ thống được đề tài quan niệm theo nghĩa rộng như sau:
Đối tượng GV gồm:
- Những GV tham gia giảng dạy Toán trên lớp truyền thống.
- Những GV tham gia quá trình thiết kế, biên soạn HLĐT, tổ chức tự học, trao đổi giải đáp thắc mắc, kiểm tra, đánh giá kết quả tự học của HS thông qua các chức năng của hệ thống.
- Những HS hỗ trợ bạn qua hệ thống trong quá trình tự học (HS đảm nhiệm vai trò của GV).
- GV “ảo”: Bản thân HLĐT và một số chức năng của hệ thống trong một phạm vi nào đấy đóng vai trò là một người “GV ảo”, luôn có mặt bên cạnh và hỗ trợ, cung cấp thông tin phản hồi đến HS.