Định vị robot sử dụng công nghệ truyền thông ánh sáng nhìn thấy được kết hợp với bộ lọc Kalman

3.1.1. Cập nhật vị trí

Mô hình động học (Kinematic model) mô tả sự ảnh hưởng của các hành động điều khiển lên cấu hình động học của robot. Cấu hình của một robot di động thông thường được biểu diễn bởi sáu biến bao gồm: tọa độ ba chiều Đề các (x, y, z) và ba góc Ơ-le (, φ, ψ). Tuy nhiên, trong giới hạn của nghiên cứu này, robot chỉ di chuyển trên mặt phẳng sàn, cho nên trạng thái động học của robot được giản lược lại còn ba biến bao gồm các tọa độ trong mặt phẳng hai chiều trong hệ tọa độ toàn cục và góc định hướng của robot. Các biến này tạo thành một véc-tơ trạng thái được minh họa trong hình 3.1a.

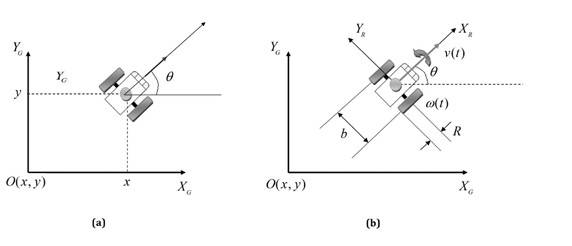
Hình 3.1. Mô hình robot hai bánh vi sai a) Trạng thái của hệ thống robot b) Robot trong hệ tọa độ địa phương và toàn cục

Hình 3.1b minh họa mô hình robot hai bánh vi sai được sử dụng trong luận văn này. Mô hình này được xét trong hệ tọa độ địa phương có gốc tọa độ đặt ở trọng tâm robot ) và trong hệ tọa độ toàn cục ). Các bánh xe lái có bán kính là a và khoảng cách giữa chúng là b. Tổng thời gian di chuyển của robot di động được lấy mẫu với khoảng thời gian lấy mẫu là ∆t đủ nhỏ. Khi đó, khoảng dịch chuyển tương đối của trọng tâm robot ∆s và góc lệch tương đối của robot ∆ trong mỗi khoảng thời gian lấy mẫu ∆t được tính toán từ khoảng dịch chuyển tuyến tính của bánh xe bên trái và bên phải của robot di động:

Có thể bạn quan tâm!

Xem toàn bộ 61 trang tài liệu này.

Trong đó, các khoảng dịch chuyển tuyến tính của bánh xe bên trái và bên phải được tính từ vận tốc góc của chúng và sau mỗi một chu kỳ lấy mẫu ∆t:

Khi đó, vị trí của robot di động tại thời điểm k+1 được tính toán theo vị trí của robot, khoảng dịch chuyển tương đối của tâm của robot ∆s và góc lệch tương đối của robot ∆ tại thời điểm k trong hệ tọa độ toàn cục:

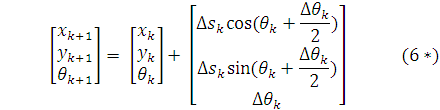
3.1.2. Sai số hệ thống

Phương trình (6*) chỉ được sử dụng trong các hệ thống lý tưởng. Trong thực tế, phương trình (6*) thường không chính xác trong các hệ thống thực tế do các tác động của một số sai số không thể tránh khỏi xuất phát từ hệ thống và môi trường. Một số nguyên nhân gây ra sự không hoàn hảo cho mô hình robot di động như bánh xe bị méo, các động cơ không đồng nhất, độ phân giải của các encoder của động cơ thấp. Các sai số trên có đặc tính tích lũy do đó nó có thể làm mất tính ổn định của các hệ thống trong thực tế. Trong phần này, chúng ta sẽ thực hiện mô hình hóa các sai số trên để có thể áp dụng bộ lọc Kalman mở rộng nhằm loại trừ chúng. Chúng ta giả sử rằng có thể mô hình hóa sai số hệ thống liên quan tới độ dịch chuyển tương đối của trọng tâm robot bằng một véc-tơ sai số ngẫu nhiên có phân bố Gauss độc lập và có giá trị trung bình bằng 0:

Trong đó, và lần lượt là các biến ngẫu nhiên biểu diễn sai số trong chuyển động của các bánh xe. là giá trị trung bình của véc-tơ :

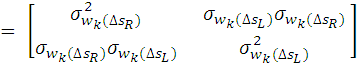
Ma trận được gọi là ma trận hiệp phương sai của sai số ngẫu nhiên . Do chúng ta đã giả sử rằng sai số này là độc lập nên các phần tử nằm ngoài đường chéo chính của ma trận hiệp phương sai bằng 0. Ma trận đồng thời phụ thuộc vào khoảng dịch chuyển tuyến tính của các bánh xe và và độ trượt của mặt sàn. Do đó, ma trận được thành lập như sau:

Trong đó, và lần lượt là hệ số tương tác giữa bánh xe và mặt sàn.

Véc-tơ sai số ngẫu nhiên được thêm vào độ dịch chuyển tương đối của trọng tâm robot ∆s và góc lệch tương đối của robot ∆ tại thời điểm k trong các hệ thống thực tế như sau:

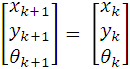
Khi đó vị trí của robot di động tại thời điểm k+1 trong thực tế được biểu diễn lại như sau:

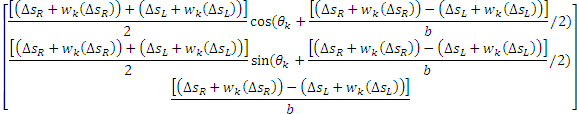
3.2. Mô hình phép đo

Mô hình phép đo lý tưởng

Giả sử trong trường hợp không có sai số, phép đo đơn giản là một véc-tơ chứa các biến tương ứng với trạng thái của robot di động :

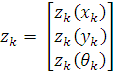
Chúng ta có mô hình phép đo tại thời điểm k là tọa độ của robot được cung cấp bởi phương pháp định vị kết hợp giữa AOA và RSS dựa trên công nghệ VLC và hướng của robot được cung cấp cảm biến gia tốc trọng trường:

Trong đó, h(.) là hàm biểu diễn mối quan hệ giữa phép đo và trạng thái của robot tại cùng thời điểm. Chúng ta có thể biểu diễn một cách đơn giản bởi công thức sau:

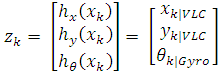
3.3. Bộ lọc Kalman

Trong phần này, chúng ta sẽ nghiên cứu việc áp dụng bộ lọc Kalman mở rộng nhằm nâng cao hiệu suất của phương pháp định vị sử dụng công nghệ VLC - phương pháp định vị kết hợp AOA-RSS.

Hình 3.3 minh họa hoạt động của bộ lọc Kalman cơ bản trong các ứng dụng thông thường. Trong đó, hệ thống trong hình có các đầu vào gồm: một tín hiệu điều khiển và các sai số hệ thống có phân bố Gauss. Các thiết bị đo đạc sẽ cung cấp các phép đo trạng thái của hệ thống với các sai số có phân bố Gauss. Bộ lọc Kalman thực chất là một kỹ thuật toán học nhằm tạo ra sự ước lượng tối ưu cho trạng thái hệ thống dựa trên các thông tin từ hệ thống và các thiết bị đo đạc.

Hình 3.4 minh họa cách thức hoạt động của bộ lọc Kalman trong vai trò bộ ước lượng cho phép định vị robot trong hai bước: ước đoán vị trí và hiệu chỉnh vị trí. Trong bước thứ nhất, robot thu thập dữ liệu từ encoder để tính toán vị trí của robot. Cùng thời điểm đó, các cảm biến bao gồm cảm biến VLC và Gyro sẽ thực hiện việc đo đạc vị trí của robot. Các thông tin về vị trí robot được tính toán từ encoder và cảm biến được kết hợp với nhau để ước định vị trí robot tối ưu. Hai bước trên sẽ được thảo luận kỹ trong các tiểu mục dưới đây.

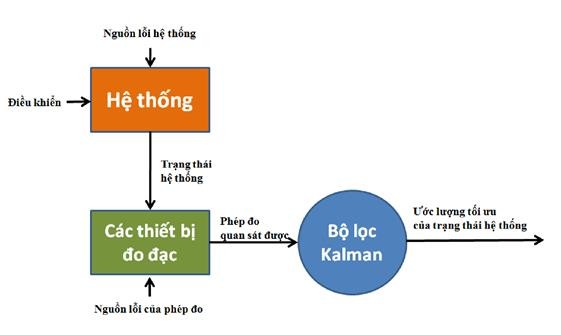
Hình 3.2. Ứng dụng thông thường của bộ lọc Kalman

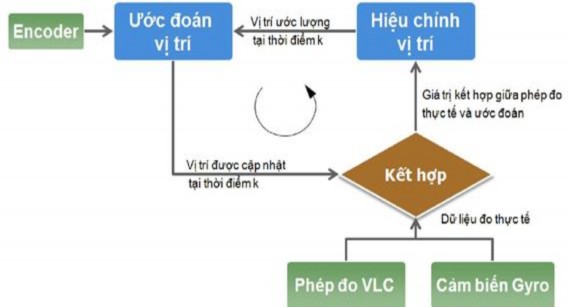
Hình 3.3. Sơ đồ minh họa ứng dụng của bộ lọc Kalman trong định vị robot

3.3.1. Ước đoán vị trí

Các phương trình của bước ước đoán vị trí tại thời điểm k+1:

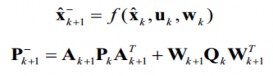
Trong đó, là vị trí ước lượng tiên nghiệm của robot tại thời điểm k+1 được ước đoán từ vị trí trước đó của nó tại thời điểm k và sự di chuyển của robot từ thời điểm k+1 đến thời điểm k dưới tác động của véc-tơ điều khiển . Hàm f(.,.,.) là hàm phi tuyến biểu diễn hệ thống dẫn động của robot. là giá trị ước lượng tốt nhất của sai số hệ thống với ma trận hiệp phương sai . Ma trận là ma trận Jacobin chứa các đạo hàm riêng của hàm theo các biến của véc-tơ trạng thái :

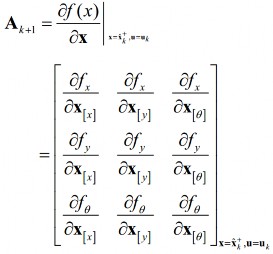
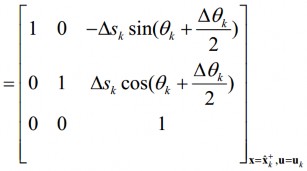
Ma trận là ma trận Jacobin chứa các đạo hàm riêng của hàm theo véc-tơ điều khiển :

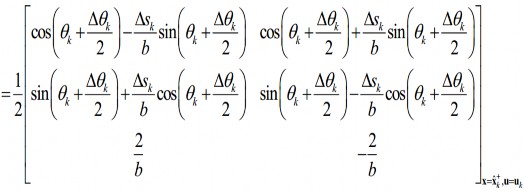
Hai ma trận trên tính toán các sự thay đổi tương đối của các biến trạng thái khi vị trí ước lượng của robot trước đó và véc-tơ điều khiển đầu vào thay đổi. Ma trận là ma trận hiệp phương sai của sai số hệ thống.

3.3.2. Hiệu chỉnh vị trí

Các phương trình của bước hiệu chỉnh vị trí tại thời điểm k+1:

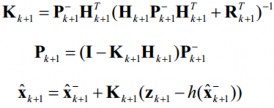
Trong đó, là véc-tơ chứa giá trị đo đạc vị trí của robot được thu thập từ các cảm biến (cảm biến VLC và Gyro) tại thời điểm k+1. Ma trận là ma trận Jacobin chứa các đạo hàm riêng của hàm biểu diễn phép đo phi tuyến h(.) theo véc-tơ vị trí ước lượng tiên nghiệm :

Có thể dễ dàng thấy trong công thức trên, ma trận Jacobin chỉ chứa các hằng số, do đó chúng ta không cần phải tính toán lại sau mỗi thời điểm. Ma trận là ma trận hiệp phương sai của véc-tơ sai số Gauss . Trong đó, phương sai của sai số trong phép đo AOA-RSS là 0.0036. Độ chính xác của cảm biến Gyro là tương ứng với phương sai của sai số này là 0.0028 trong hệ đơn vị rad.

Ngoài ra, là trọng số của bộ lọc Kalman; ma trận là ma trận hiệp phương sai của sai số trong bước hiệu chỉnh vị trí. Cuối cùng, là vị trí ước lượng hậu nghiệm của robot được ước tính từ giá trị tiên nghiệm trong bước ước đoán vị trí bằng việc cộng thêm một lượng điều chỉnh bằng tích của độ sai lệch giữa hai phép đo thu được từ encoder và các cảm biến và trọng số .

3.4. Tóm tắt chương ba

Trong chương này, chúng ta đã thảo luận về các mô hình hệ thống và mô hình phép đo sử dụng phương pháp định vị dựa trên công nghệ VLC và cảm biến Gyro. Đồng thời, chúng ta cũng đã mô hình hóa các sai số hệ thống và sai số của phép đo. Các sai số này có phân bố Gauss, độc lập và có giá trị trung bình bằng 0, được sinh ra do các yếu tố từ hệ thống và môi trường.

Để nâng cao độ chính xác của thuật toán định vị kết hợp AOA-RSS, chúng ta sử dụng bộ lọc Kalman mở rộng để kết hợp nó với thông tin về vị trí từ hệ thống nhằm đạt được một vị trí ước lượng tốt nhất. Trong phần nội dung của chương này đã trình bày hai bước trong thuật toán bộ lọc Kalman mở rộng: ước định vị trí và hiệu chỉnh vị trí để tìm vị trí ước lượng tối ưu của robot di động. Đây là nội dung chính của chương ba cũng như của toàn bộ luận văn này.