Các Định Lý Hợp Vận Tốc, Hợp Gia Tốc

(nghĩa là tính toán trong hệ quy chiếu cố định) được gọi là vận tốc tuyệt đối, gia tốc tuyệt đối. Ký hiệu va , aa .

Ta có:

v

d O1 M dr

(6-1)

(6-2)

a

dt

dt

aa 1

d 2 O M

d 2r

(1.40)

(1.41)

dt 2 dt



e

k

j

i

O

x

b. Chuyển động tương đối

Chuyển động của điểm M đối với hệ quy chiếu động Oxyz được gọi là chuyển động tương đối. Vận tốc, gia tốc z

điểm M trong chuyển động tương đối (nghĩa là tính toán trong y

hệ quy chiếu động) được gọi là vận tốc tương đối, gia tốc



tương đối. Ký hiệu:

vr , ar . Ký hiệu

i , j , k

là các véc tơ đơn

vị trên các trục Ox, Oy, Oz. Tọa độ của điểm M trong hệ quy chiếu động là x, y, z. Khi đó, ta có:



OM xi yj zk

Theo định nghĩa trên biểu thức của véc tơ vr , ar

có dạng:

Hình 1.43



dx 

i 

dt

dy 

j 

dt

xem i, j, k là các véc tơ hằng số:

v

a

d OM d OM 

dt





dt





dz 

k

dt

(1.42)

ar 

d 2 O M

dt 2

2

d x

dt 2 i 

d 2 y

dt 2

d 2 z

j k

dt 2

(1.43)

c. Chuyển động theo

Chuyển động của hệ quy chiếu động Oxyz đối với hệ quy chiếu cố định O1x1y1z1 gọi là chuyển động theo.

Để có thế thiết lập biểu thức của vận tốc theo, gia tốc theo, ta đưa vào khái niệm trùng điểm. Gọi điểm M* của hệ quy chiếu động mà ở thời điểm khảo sát có cùng vị trí với điểm M là trùng điểm của điểm M tại thời điểm đó. Như thế, ở mỗi thời điểm, điểm M trùng với một điểm M* nào đó của hệ quy chiếu động.

Vận tốc, gia tốc tuyệt đối của trùng điểm M* tại thời điểm khảo sát (nghĩa là tính toán trong hệ quy chiếu cố định) được gọi là vận tốc theo, gia tốc theo của điểm

M tại thời điểm đó. Ký hiệu: ve , ae .

Gọi x*, y*, z* là tọa độ của trùng điểm M* trong hệ quy chiếu động Oxyz (x*, y*, z* là các hằng số). Ta có:



O1M * O1O OM * O1O x * i y * j z * k

Theo định nghĩa:

v v

dO1M * dO1O x * di y * d j z * d k

e M *

dt dt dt dt dt

d 2 O M * d 2 O O d 2 i d 2 j

d 2 k

ae aM * 11x *

y *

z *

dt2

dt2

dt2

dt2

dt2

Do x(t) = x*(t), y(t) = y*(t), z(t) = z*(t), nên ta có

v dO1O x di y d j z d k

(1.44)

e dt dt dt dt

d 2 O O d 2 i d 2 j

d 2 k

ae 1x dt 2

dt 2

y dt 2

z dt 2

(1.45)

Trong các bài toán áp dụng để tính vận tốc theo, gia tốc theo ta tưởng tượng dừng điểm M lại trên hệ quy chiếu động. Sau đó tính toán vận tốc, gia tốc của điểm M do chuyển động của hệ động đối với hệ quy chiếu cố định gây ra.

3. Các định lý hợp vận tốc, hợp gia tốc

a. Định lý hợp vận tốc

Ở mỗi thời điểm, vận tốc tuyệt đối của điểm bằng tổng hình học các vận tốc tương đối và vận tốc theo của nó.

va vr ve

Chứng minh: Theo hình 1.42 ta có:



O1M O1O OM O1O xi yj zk

Đạo hàm biểu thức trên ta được:

(1.46)

dO1M

dO1O x di

y d j z d k dx i dy

j dz k

dt dt dt dt dt dt dt dt

Chú ý đến (1.40), (1.42) và (1.44) ta suy ra:

va vr ve

b. Định lý hợp gia tốc

Ở mỗi thời điểm, gia tốc tuyệt đối của điểm bằng tổng hình học của gia tốc tương đối, gia tốc theo và gia tốc Côriôlit.

aa ar ae ac

Khi hệ động Oxyz chuyển động tịnh tiến:

ac  0

(1.47)

thì

Khi hệ động Oxyz chuyển động quay quanh một trục cố định với vận tốc góc 

ac  2e vr

Chứng minh: Đạo hàm hai lần biểu thức:



O1M

O1O xi yj zk

Ta được:

d 2 O M d 2 O O d 2 i d 2 j d 2 k d 2 x d 2 y

d 2 z

11x y z i j 

dt 2 dt 2 dt 2 dt 2 dt 2 dt 2 dt 2

dx d i dy d j dz d k 

dt 2

2







dt dt dt dt dt dt 

Chú ý đến (1.41), (1.43) và (1.45) ta có:

aa ar ae ac

Trong đó: ac =

dx di





2 

dy d j

dz d k 





gọi là gia tốc Côriôlit.

dt dt dt dt dt dt 



Khi hệ quy chiếu động Oxyz chuyển động tịnh tiến, các véc tơ đơn vị i , j, k là

các véc tơ hằng. Do đó véc tơ

ac  0 .

Khi hệ quy chiếu chuyển động quay quanh một trục cố định ∆ (Hình 1.43), ta lấy điểm O trên trục ∆ làm gốc trên hệ quy chiếu ấy. Theo công thức tính vận tốc Ơle

Ta có:



dk 

di 

i ; dj 

j;

k

dt e

dt e

dt e

Từ đó ta suy ra:

a  2

dxdydz

 2v

(1.48)



c e dt i

j k e r

dt dt 

Chú ý: Khi làm các bài tập ta có thế sử dụng quy tắc thực hành để xác định véc tơ gia tốc Côriôlit như sau:

e

e

ac

vr



v'r ac

vr

Hình 1.44

Hình 1.45

Có thể bạn quan tâm!

• Cơ học ứng dụng - 2
• Khảo Sát Chuyển Động Của Các Điểm Thuộc Vật
• Định Nghĩa Chuyển Động Tuyệt Đối, Tương Đối Và Chuyển Động Theo
• Thông Số Làm Việc Chủ Yếu Của Bộ Truyền Bánh Răng
• Lực Liên Kết - Lực Hoạt Động - Phản Lực Liên Kết
• Định Luật 4: Định Luật Tác Dụng Và Phản Tác Dụng

Xem toàn bộ 180 trang tài liệu này.

- Khi điểm M chuyển động trên một mặt phẳng thì

e vr . Khi đó ta quay vr

theo chiều quay của e đi một góc 90o, ta sẽ được phương và chiều của véc tơ ac . Độ lớn của nó được tính theo công thức ac = 2ωevr (Hình 1.44).

- Khi điểm M không chuyển động trên một mặt phẳng. Trong mặt phẳng vr,e

, chiếu vr

lên mặt phẳng vuông góc với e

ta được véc tơ

v'r . Ta có

v'r = vr.sinα. Sau

đó quay

v'r

một góc 90o theo chiều của e

ta được phương và chiều của

ac . Độ lớn

của nó (Hình 1.45)

a  2v'  2v

sin

c e r e r

Ví dụ 1.7: Hai bờ sông của một con sông song song với nhau. Chiều rộng của dòng sông là h. Dòng sông chảy với vận tốc v có trị số không đổi. Một người lái thuyền sang ngang với vận tốc tương đối là u . Xác định hướng của vận tốc u để cho thời gian sang sông là ngắn nhất. Với điều kiện đó, xác định vị trí cập bến của thuyền. (Hình 1.46).

Bài giải:

Vật điểm khảo sát là con thuyền. Hệ quy chiếu chuyển động là dòng nước, hệ quy chiếu cố định là một mốc ở bờ sông. Khi đó con thuyền sẽ tham gia hai chuyển động: chuyển động tương đối với

vận tốc

vr u

và chuyển động với vận

tốc ve v .

Theo định lý hợp vận tốc:

va u v

Hình 1.46

Chiếu đẳng thức này lên các trục tọa độ ta được:

vax u sinv; vay u cos

Từ đó tích phân lên, với điều kiện đầu x(0) = 0; y(0) = 0, ta được:

x u sinvt; y u cost

Khi thuyền cập bến: y = (ucosα)t = h. Vậy thời gian sang sông là:

t h

u cos

Khi α = 0  cos 1 t h

min u

Vị trí cập bến của con thuyền sẽ bị lùy một đoạn so với điểm xuất phát là:

x v h

u

1.3.2. Hợp chuyển động của vật rắn

1.3.2.1 Hợp hai chuyển động tịnh tiến

Định lý: Hợp hai chuyển động tịnh tiến là một chuyển động tịnh tiến với véc tơ vận tốc bằng tổng hình học hai véc tơ vận tốc của các chuyển động đã cho.

Giả sử có vật rắn chuyển động tịnh tiến đối với hệ động, vận tốc

u1 ; trong khi

hệ động cũng tịnh tiến đối với hệ cố định, vận tốc

u2 . Ta xét một điểm M bất kỳ trên

vật. Vận tốc tuyệt đối của M được xác định như sau:

vaM veM vrM

Vì chuyển động tương đối và chuyển động theo đều là tịnh tiến:

vrM u1;veM u2

Nên:

vaM

u1 u2

Công thức này đúng cho mọi điểm thuộc vật. Trong chuyển động tuyệt đối mọi điểm thuộc vật tại cùng một thời điểm có cùng vận tốc, vậy đó là chuyển động tịnh tiến. Vận tốc tịnh tiến là:

u u1 u2

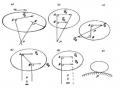
1.3.2.2 Hợp hai chuyển động quay quanh trục song song

1. Hai chuyển động quay cùng chiều

Định lý: Hợp hai chuyển động quay song song cùng chiều là một chuyển động quay song song cùng chiều với các chuyển động đó. Chuyển động tổng hợp có trục quay chia trong đoạn nối hai trục đã cho thành những đoạn tỉ lệ nghịch với các vận tốc góc và có trị số vận tốc góc bằng tổng các vận tốc góc đã cho.

Cho 2 chuyển động quay như hình 1.47, trục quay của chuyển động tổng hợp đi qua C nằm trong đoạn nối O1O2 với:

CO1 CO2

2 ;

1

1 2 ;

2. Hai chuyển động quay ngược chiều

Định lý: Hợp hai chuyển động quay song song ngược chiều là một chuyển động quay song song cùng chiều với chuyển động quay có vận tốc góc lớn. Chuyển động tổng hợp có trục quay chia ngoài đoạn nối hai trục đã cho thành những đoạn tỉ lệ nghịch với các vận tốc góc và có trị số vận tốc góc bằng hiệu các vận tốc góc đã cho.

ve

vr

O2

M

C O1





vo1

C

O1

vr

M

ve

O2

O1 C





O1 C

vo1

Hình 1.47 Hình 1.48

Cho 2 chuyển động quay như hình 1.48, trục quay của chuyển động tổng hợp đi qua C nằm trong đoạn nối O1O2 với:

CO1 CO2

2 ;

1

1 2 (Giả sử 1 >2)

3. Hai chuyển động quay ngược chiều cùng tốc độ

Định lý: Hợp hai chuyển động quay song song ngược chiều cùng tốc độ là một chuyển động tịnh tiến. Vận tốc tịnh tiến bằng tích véc tơ của véc tơ nối trục quay theo với trục quay tương đối và véc tơ vận tốc góc tương đối, nghĩa là:

u O2O1 1

Chú ý: ta có thể giải thích định lý trên một

cách trực tiếp. Xét một đoạn thẳng thuộc vật. Vì rằng hai chuyển động quay tương đối và quay theo có chiều trái nhau và cùng tốc độ, do đó trong quá trình chuyển động đoạn thẳng không bị lệch hướng (trong chuyển động tương đối đoạn thẳng bị quay đi một góc bao nhiêu thì chuyển động theo đoạn thẳng lại được quay trả lại một góc bấy nhiêu). Vậy vật có chuyển động tịnh tiến.

* Nhận xét



'





Hình 1.49

Nếu dựng véc tơ trên trục quay của chuyển động tổng hợp; biểu diễn cho trục, chiều và tốc độ của chuyển động đó – và xem các véc tơ vận tốc góc biểu thị cho các chuyển động quay – thì ta nhận thấy rằng phép hợp các véc tơ vận tốc góc cho kết quả tương tự như phép hợp hai lực song song; nghĩa là nói chung hai véc tơ vận tốc thì được một véc tơ vận tốc góc:

1 2

đặt ở điểm xác định như hợp lực, trừ trường hợp hai véc tơ cùng trị số trái chiều thì được một véc tơ vận tốc (biểu diễn cho chuyển động tịnh tiến).

O2

O1



F

B

A



M



R

 v



R

O2 O1 C

RF

B C A C

FF

Hình 1.50

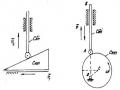
Ví dụ 1.8

Tay quay OA quay ngược chiều kim đồng hồ quanh O với tốc độ no = 120 vòng/phút.

Trong khi đó bánh xe II cũng quay quanh O theo chiều ngược kim đồng hồ với tốc độ n2 = 180 vòng/phút.

O A





Tìm vận tốc góc so với mặt bảng cố định và so với tay quay OA của bánh xe I gắn vào mút A của tay quay và ăn khớp với bánh xe II. Cho biết các bánh xe có bánh kính R1 = 2R2

Bài giải

Chuyển động của bánh xe I đối với tay quay rò

ràng là một chuyển động quay (vì tâm A gắn cố định trên tay quay). Tay quay lại quay quanh O. Như thế

Hình 1.51

theo các định lý ở trên, chuyển động của bánh xe I so với mặt bảng cố định chuyển động tuyệt đối cũng là một chuyển động quay. Ở đây ta chỉ tìm đại số vận tốc góc của các chuyển động đó.

Muốn thế, ta xét đồng thời chuyển động của bánh xe I và II, nhận tay quay làm hệ động.

Vì rằng hai bánh xe I và II cũng có tâm gắn cố định trên tay quay (ở O và A), lại ăn khớp với nhau nên có thể áp dụng công thức về tỉ số truyền quay:

, R



12

1

, R

2

(1)

1 2

, , ,

là đại số vận tốc góc tương đối của các bánh xe so với tay quay (lấy dấu

trừ vì hai bánh xe ăn khớp ngoài).

Gọi o là đại số vận tốc góc của tay quay, và 1 , 2

đối của các bánh xe I và II, ta có:

là đại số vận tốc góc tuyệt

1 o

2 o

1

,

2

,

Như thế, công thức (1) viết được:

1 o

2 o

R2

R1

gọi là công thức Vilixơ. Dựa vào o , 2 đã biết ta có thể tìm được 1 :

1 o

2

o2



R

R

(2)

Theo bài ra tay quay OA và bánh xe II quay đều theo chiều dương nên:

o

và 2

no

30

n2

30

 4

 6

rad/s

rad/s

như thế thay vào (2):

 46 41  3

1 2

rad/s



1 1

và ,  3 4

o

rad/s

Bánh xe 1 quay đối với bảng theo chiều dương, còn nhìn từ tay quay thì thấy bánh xe 1 quay theo chiều âm 1 < 0.

Chú ý: cơ cấu ta vừa xét (cho hai vận tốc góc, có hai

bậc tự do) thường gọi là cơ cấu vi sai.

Nếu bánh xe II cố định thì đó là cơ cấu hành tinh (cho biết một vận tốc góc, có một bậc tự do). Thực tế ta có thể gặp những cơ cấu này ở dạng phức tạp hơn (gồm nhiều bánh xe ăn khớp liên tiếp hay gắn không gian), để giải, nói chung ta đều





b



O

c 

a



dùng công thức Vilixơ.

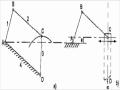
4. Hợp hai chuyển động quay quanh trục giao nhau

Hình 1.52

Định lý: Hợp hai chuyển động quay có trục giao nhau là một chuyển động quay có trục đi qua giao điểm và véc tơ vật tốc góc bằng tổng vận tốc của các chuyển động đã cho.

Cho 2 chuyển động quay như hình 1.52, trục quay của chuyển động tổng hợp đi qua O và có vận tốc góc: 1 2

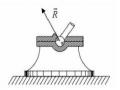
Ví dụ 1.9

Tay quay OA quay quanh trục thẳng đứng vận tốc góc ωo làm bánh xe hình nón BC lăn không trượt trên bánh xe cố định nằm ngang. Tìm vận tốc góc đối với tay quay và đối với bánh xe cố định của bánh xe BC. Tìm vận tốc góc của điểm C cao nhất của

bánh xe đó, cho biết bán kính của nó là R, AOB .

Bài giải

Theo bài ra, tay quay quay quanh trục thẳng đứng. Đối với tay quay, bánh xe BC rò ràng lại có chuyển động quay mà trục là OA. Như thế ở đây ta có bài toán hợp hai chuyển động quay trục giao nhau, chuyển động tổng hợp của bánh BC là một chuyển động quay mà trục quay đi qua



r O

Hình 1.53

C

vA

A

 R B