Bản Chất Và Tác Dụng Của Phương Pháp

được-hay là một chỉ báo. Đây có thể là nguyên nhân hoặc là kết quả của biến tiềm ẩn “chất lượng học tập”. Điểm 10-có thể là chỉ báo nguyên nhân của chất lượng học tập tốt, đồng thời cũng có thể là kết quả của “chất lượng học tập tốt”. Một ví dụ khác minh họa rõ hơn điều này. Rubenstein (1986) [29] nghiên cứu sự tò mò của học sinh thông qua một thang giải điểm đồng ý, không đồng ý với câu nói “Tôi muốn biết cái máy này chạy như thế nào” hoặc “tôi muốn thử loại đồ ăn mới này”. Việc đồng ý/không đồng ý với các câu nói này là kết quả của việc đối tượng nghiên cứu tò mò hay không tò mò, và do vậy, thang điểm thể hiện sự đồng ý của đối tượng điều tra với các câu nói trên chính là các “chỉ báo kết quả” của biến tiềm ẩn “sự tò mò”. Hầu hết các mô hình về biến tiềm ẩn đều được xây dựng trên cơ sở “chỉ báo kết quả”, có nghĩa là các chỉ báo là kết quả của biến tiềm ẩn. Việc nhầm lẫn giữa “chỉ báo nguyên nhân” và “chỉ báo kết quả” sẽ dẫn đến mô hình sai và tất nhiên là những kết luận sai (Bollen, 2003) [3].

2.2. MỘT SỐ PHƯƠNG PHÁP THỐNG KÊ NGHIÊN CỨU VỀ CÁC BIẾN TIỀM ẨN

2.2.1. Phương pháp hồi qui bội

2.2.1.1 Bản chất và tác dụng của phương pháp

Phương pháp hồi qui bội được Pearson sử dụng lần đầu tiên năm 1908. Phân tích hồi qui là phương pháp thống kê nghiên cứu mối liên hệ của một biến (gọi là biến phụ thuộc hay là biến được giải thích) với một hay nhiều biến khác (gọi là biến độc lập hay biến giải thích).

Mục đích của phân tích hồi quy là ước lượng giá trị của biến phụ thuộc trên cơ sở giá trị của các biến độc lập đã cho. Còn phân tích tương quan là đo cường độ kết hợp giữa các biến, nó cho phép đánh giá mức độ chặt chẽ của sự phụ thuộc giữa các biến.

Phương pháp hồi qui tương quan bội được vận dụng để nghiên cứu mối liên hệ của các yếu tố ảnh hưởng đến chất lượng dịch vụ hàng không do hành khách cảm nhận, thường được thể hiện qua biến mức độ hài lòng của hành khách. Mục tiêu của việc nghiên cứu nhằm chỉ ra các yếu tố tố nào có ảnh hưởng lớn đến mức độ hài

lòng của hành khách nhằm đưa ra các giải pháp nâng cao chất lượng của các yếu tố ảnh hưởng, với kỳ vọng sẽ nâng cao mức độ hài lòng chung.

Có thể bạn quan tâm!

Xem toàn bộ 204 trang tài liệu này.

2.2.1.2. Các bước vận dụng phương pháp hồi qui bội

Vận dụng phương pháp hồi qui bội vào nghiên cứu chất lượng dịch vụ hành khách hàng không cần đi qua năm bước như sau:

Bước 1: Lựa chọn các tiêu thức (các biến) đưa vào phân tích

Bước 2: Lựa chọn mô hình phù hợp nhất để mô hình hóa mối quan hệ giữa các biến độc lập và biến phụ thuộc. Để chọn mô hình phù hợp nhất Sử dụng các phép kiểm định để kiểm tra i) sự tồn tại thực tế của mối liên hệ giữa các biến độc lập và biến phụ thuộc thông qua kiểm định F và ii) sự phù hợp của mô hình thông qua chỉ tiêu SSE (sai số mẫu). Mô hình tốt nhất là mô hình có hệ số quyết định điều chỉnh lớn nhất và sai số mẫu nhỏ nhất. Đồng thời kiểm tra mức độ ảnh hưởng thực tế của từng biến độc lập đến biến phụ thuộc thông qua các hệ số hồi qui B và so sánh mức độ ảnh hưởng của từng biến nguyên nhân đến biến kết quả thông qua việc so sánh hệ số B chuẩn hóa. Lý do phải thực hiện rất nhiều phép kiểm định vì các kết quả tính toán được tính ra dựa trên một mẫu. Kết quả kiểm định sẽ cho phép suy rộng kết luận từ mẫu cho kết luận về tổng thể chung.

Bước 3: Loại bỏ khỏi mô hình tốt nhất các biến có hệ số B không có Sig t nhỏ hơn 0.05 hoặc 0.01 (tùy theo mức ý nghĩa được lựa chọn). Nói cách khác, không có đủ bằng chứng để bác bỏ giả thuyết rằng trên thực tế các biến này không có ảnh hưởng đến chất lượng dịch vụ hàng không chung.

Bước 4: Phân tích phần dư và phân tích đa cộng tuyến nhằm đưa ra các điều chỉnh cần thiết cho mô hình

Bước 5: Kết luận về mức độ ảnh hưởng và dự đoán các mức độ của biến phụ thuộc trong tương lai.

Các điểm lưu ý trong từng bước:

Bước 1: Lựa chọn các biến đưa vào mô hình

Khi áp dụng hồi qui cũng như các phương pháp khác trong nghiên cứu quan hệ nhân quả, điều quan trọng đầu tiên là đưa ra mô hình lý thuyết. Việc xác định mô

hình lý thuyết được dựa trên việc phân tích định tính kết hợp với các nghiên cứu tương tự đã được thực hiện từ trước đó.

Mô hình lý thuyết trong việc nghiên cứu chất lượng dịch vụ hàng không có thể được xây dựng theo các cách tiếp cận sau:

Biến phụ thuộc là chất lượng dịch vụ cảm nhận của hành khách. Chất lượng dịch vụ có thể được biểu hiện qua chỉ báo “mức độ hài lòng của quí khách” với thang đo Likert 1-5 hoặc 1-7; cũng có thể được đo qua các chỉ báo khác như “ quí khách sẽ tiếp tục lựa chọn VNA” với thang đo Likert, trong đó 5 hoặc 7 là rất đồng ý với mệnh đề trên và 1 là hoàn toàn không đồng ý. Việc khách hàng nhất định sẽ chọn VNA là một chỉ báo cho việc hài lòng và việc nhất định không chọn sẽ là một chỉ báo của việc rất không hài lòng. Tương tự như vây, chỉ báo “quí khách chắc chắn sẽ giới thiệu VNA với người thân và bạn bè” với thang đo Likert 1-5 hoặc 1-7 cũng phản ánh mức độ hài lòng của hành khách. Do vậy, biến phụ thuộc có thể là một trong 3 chỉ báo ở trên, hoặc là tập hợp của cả ba chỉ báo. Trường hợp chọn biến phụ thuộc là tập hợp chỉ báo sẽ được đề cập ở phần sau.

Biến độc lập là các yếu tố ảnh hưởng đến chất lượng dịch vụ hành khách. Tuy nhiên, có nhiều cách tiếp cận làm cơ sở cho việc lựa chọn biến độc lập. Thứ nhất, xây dựng biến độc lập có thế dựa trên qui trình cung ứng dịch vụ hàng không từ lúc đặt vé máy bay đến lúc kết thúc chuyến bay như đã trình bày trong chương 1. Ngoài cách tiếp cận này, các biến độc lập cũng có thể được thiết kế dựa trên năm khía cạnh theo phương pháp Servqual. Cách này được rất nhiều các nhà nghiên cứu áp dung khi nghiên cứu về sự hài lòng của khách hàng biểu hiện thông qua chất lượng dịch vụ cảm nhận. Thông thường, số biến độc lập đưa vào mô hình rất lớn, do vậy, khả năng đa cộng tuyến giữa các biến độc lập khá lớn. Như vậy việc kết hợp một số biến có mức độ tương quan cao với nhau là cần thiết để đảm bảo tính chính xác của mô hình.

Bước 2: Lựa chọn mô hình hồi qui

Phương pháp thường được sử dụng nhất trong lựa chọn mô hình hồi qui là phương pháp bình phương nhỏ nhất. Mục tiêu của phương pháp này là lựa chọn ra

một mô hình có tổng bình phương các chênh lệch giữa giá trị thực tế và giá trị tính theo mô hình là nhỏ nhất. Mối quan hệ giữa biến phụ thuộc và biến độc lập có thể được biểu diễn như sau:

E(Y / X1 , X2,..., Xk) 0 1X1 2X2 ... kXk

Trong đó:

Y: biến phụ thuộc

X1 , X2 ,..., Xk : là các biến độc lập

(2.1)

0 là hệ số tự do (hệ số chặn)

1 ,2 ,...,k : gọi là các hệ số hồi quy riêng Đối với mỗi giá trị Yi của y ta có

Yi  E(Y / X1 , X2,..., Xk) i

(2.2)

Trong đó i

gọi là sai số ngẫu nhiên

Trong mô hình hồi qui bội trên, các hệ số mang ý nghĩa như sau:

0 là giá trị trung bình của y khi

X1  X2  ...  Xk  0

i (i  1, k)

nói lên sự thay đổi trung bình của biến phụ thuộc Y khi biến giải

thích Xi thay đổi một đơn vị trong điều kiện các biến giải thích khác không thay đổi.

Lý do cần phải thực hiện các phép kiểm định là do các nghiên cứu của mẫu được sử dụng để suy rộng cho toàn bộ tổng thể chung. Mô hình hồi quy (2.1) có thể được ước lượng thông qua môt mẫu ngẫu nhiên. Phương trình hồi quy của mẫu có dạng:

Yˆ b0 b1X1 b2X2 ...  bkXk

(2.3)

Trong đó Khi đó:

bi (i  0,1,..., k) là các ước lượng tương ứng của i (i  0,1,..., k)

Yi  b0 b1X1  b2X2  ...  bkXk

Với ei là phần dư. ta sẽ có:

 ei

(2.4)

ei Yi Yˆ

 Yi  b0 b1X1  b2X2 ...  bkXk

(2.5)

Áp dụng phương pháp bình phương nhỏ nhất để tính giá trị của các tham số

b0, b1 , b2,..., bk

sao cho:

SSE e2Y  b

 b X

 ...  b X

2 min

i1

0 1 1 2 2 k k

SSE chính là tổng bình phương của các chênh lệch giữa giá trị thực tế và giá trị theo mô hình, hay nói cách khác SSE phản ánh sai số của mô hình. Mô hình tốt nhất sẽ là mô hình có SSE min.

Tuy nhiên, SSE chỉ là một thông tin để lựa chọn mô hình tốt nhất. Một thông tin nữa là hệ số quyết định R bình phương hay còn gọi là hệ số quyết định. Mức độ một hay nhiều biến độc lập ảnh hưởng lên biến phụ thuộc được biểu hiện thông qua hệ số tương quan R, là căn bậc hai của hệ số quyết định. Hệ số quyết định thể hiện phần trăm biến thiên của biến phụ thuộc do các biến độc lập mô hình

gây ra. Nói cách khách, hệ số quyết định cho biết các biến độc lập trong mô hình có ảnh hưởng lớn hay nhỏ đến sự biến động của biến phụ thuộc Y. Giá trị của R2 chạy từ 0-1. Như vậy, một hàm hồi qui có hệ số quyết định 0.6 có nghĩa là các biến độc lập gây ra 60% sự biến động của Y, và 40% sự biến động của Y là do các nhân tố ngoài mô hình gây ra. Do vậy, hệ số quyết định lớn là một yếu tố để lựa

chọn mô hình tốt nhất.

Tuy nhiên, trong mô hình hồi qui đa biến, cần lưu ý đến hệ số quyết định điều chỉnh. Hệ số này chịu ảnh hưởng của số biến giải thích có trong mô hình. Do đó, nếu tăng số biến giải thích trong mô hình thì hệ số xác định bội cũng tăng cũng tăng. Điều đó ảnh hưởng đến tính chính xác của viêc lựa chọn mô hình phù hợp nhất cho mối quan hệ. Điều này dẫn đến việc cần phải đưa ra một hệ số điều chỉnh để đảm bảo tính so sánh được giữa các mô hình. Công thức tính hệ số xác định điều

SSE (n  k  1)

SS(Y) (n  1)

chỉnh

R 2 như sau:

R 2  1 

(2.6)

hay

R 2  1 (n 1) (1  R 2 ) (n  k  1)

(2.7)

Trong đó: k là số biến độc lập, và là bậc tự do của SSR n-k-1 là bậc tự do của SSE

n-1 là bậc tự do của SS(Y)

R 2

Để đánh giá mức độ chặt chẽ của mối liên hệ tuyến tính giữa biến phụ thuộc Y với các biến độc lập Xi (i = 1, k ) người ta dùng hệ số tương quan bội, ký hiệu R.

SSR

SS(Y)

R 

và 0  R  1

(2.8)

nếu R = 0 thì không tồn tại liên hệ tuyến tính R = 1 liên hệ hàm số

R +/-1 mối liên hệ càng chặt chẽ

Một phép kiểm định nữa phải thực hiện là kiểm định giả thiết trên thực tế không tồn tại quan hệ giữa các biến độc lập với biến phụ thuộc, mặc dù hệ số quyết định của mô hình tính ra từ mẫu nghiên cứu có giá trị khác 0.

Giả thiết kiểm định:

Ho : 1 2 ... k  0

H1: ít nhất có một i

khác 0

Tiêu chuẩn kiểm định

SSR k

SSE n  (k  1)

F 

F có phân phối F(k; [n-(k+1)].

(2.9)

SSR (Yˆi Y)2: là tổng của bình phương các chênh lệch giữa trị số lý thuyết theo phương trình hồi qui mẫu với trị số bình quân của biến phụ thuộc Y. Chỉ

tiêu này được gọi ngắn gọn là tổng các độ lệch bình phương hồi qui.

SSE (Yi

 Yˆi)

: là tổng của bình phương các chênh lệch giữa các trị số

thực tế và trị số lý thuyết của biến phụ thuộc Y phần dư. Chỉ tiêu này được gọi ngắn gọn là tổng các độ lệch bình phương phần dư

k: số lượng các biến độc lập

F lớn hơn một giá trị F* tương ứng với mức ý nghĩa an-pha 0.05 hoặc 0.01 sẽ giúp bác bỏ giả thiết Ho. Điều đó có nghĩa là có ít nhất một trong các biến độc lập đang nghiên cứu có ảnh hưởng lên biến phụ thuộc, hay nói cách khác là tồn tại mối liên hệ nhân quả giữa các biến độc lập đang nghiên cứu với biến kết quả.

Bước 3: Loại bỏ khỏi mô hình các tham số không phù hợp

Tham số hồi qui trong mô hình được biểu hiện qua các kí hiệu Bi, phản ánh ảnh hưởng của từng biến độc lập lên biến kết quả. Bi chính là các ước lượng của tham số beta trong mô hình

E(Y / X1 , X2 ,..., Xk ) 0 1X1 2X2  ... kXk .

Nói cách khác, nếu beta phản ánh mức độ ảnh hưởng của từng biến độc lập lên biến phụ thuộc của toàn bộ tổng thể thì B phản ánh ảnh hưởng của từng biến độc lập lên biến phụ thuộc ở mẫu quan sát. Do vây, có thể dùng B để ước lượng cho beta.

Một phép kiểm định cần phải thực hiện để kiểm định xem từng biến độc lập có thực sự ảnh hưởng đến biến phụ thuộc hay không.

Giả thiết kiểm định: Ho: i =0

H1: i khác 0

Sử dụng tiêu chuẩn kiểm định t để kiểm định giả thiết trên. Giá trị của t lớn hơn giá trị t* được tính ra theo mức ý nghĩa 0.05 hoặc 0.01 cho phép bác bỏ giả thuyết Ho. Nói cách khác, thực tế biến độc lập thứ i có ảnh hưởng đến biến kết quả.

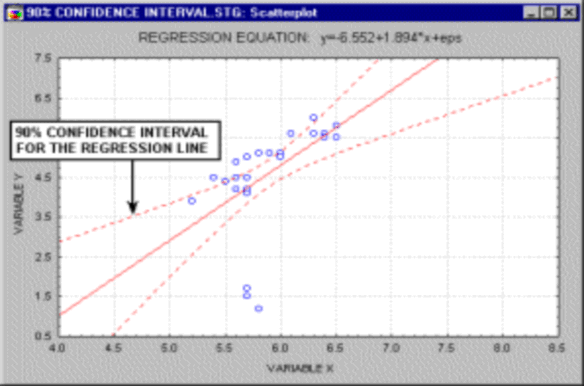
Khi sử dụng B để ước lượng cho các hệ số hồi qui beta, một khoảng tin cậy với độ tin cậy khác nhau (90%, 95% và 99%) sẽ được xây dựng. Đồ thị dưới đây minh họa 3 mô hình hồi qui; trong đo đường ở giữa là hàm hồi qui được tính ra từ mẫu và

hai hai hàm hồi qui ở trên và ở dưới là hai hàm hồi qui với hệ số beta được ước lượng từ các tham số của mẫu với khoảng ước lượng 90%.

Tuy nhiên, các biến độc lập có thể được đo với các thang đo khác nhau. Do vậy, cần thiết phải qui chuẩn các hệ số hồi qui để có thể so sánh mức độ ảnh hưởng của các biến khác nhau đến biến phụ thuộc. Ví dụ: trong các yếu tố ảnh hưởng đến chất lượng dịch vụ hàng không chung là chất lượng tiếp viên, chất lượng máy bay và chất lượng đồ ăn, uống và giải trí trên máy bay, cần thiết phải chỉ ra yếu tố nào là yếu tố ảnh hưởng lớn nhất tới chất lượng dịch vụ hành khách nói chung. Điều này có thể được trả lời thông qua hệ số B chuẩn hóa.

Bước 4: phân tích phần dư và đa cộng tuyến để điều chỉnh mô hình nếu cần thiết.

Phương pháp hồi qui được xây dựng dựa trên các giả thuyết sau:

Tính tuyến tính: phương pháp này dựa trên giả định rằng mối quan hệ giữa các biến là quan hệ tuyến tính. Trên thực tế giả thuyết này rất khó được kiểm chứng, tuy nhiên sử dụng các kĩ thuật như chuyển hóa biến (bình phương, khai căn, logarit các biến độc lập) đã giúp cho mô hình gần với tuyến tính nhất.