Bài Toán Xác Định Ma Trận Trọng Số Tối Ưu Cho Tổ Hợp Thích Nghi

1



 (n) 0

n 0

n 0 ,

A R là độ lớn, hoặc biên độ của x(n) .

x(n) .

Có thể bạn quan tâm!

• Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 1
• Các phương pháp thích nghi trong lọc nhiễu tín hiệu điện tim - 2
• Can Nhiễu Ảnh Hưởng Đến Chất Lượng Ghi Tín Hiệu Điện Tim
• Cơ Sở Toán Học Của Phương Pháp Thích Nghi Dựa Trên Thuật Toán
• Phương Pháp Thích Nghi Lọc Nhiễu Điện Áp Cho Các Tín Hiệu Y Sinh
• Kết Quả Lọc Nhiễu Đối Với Tín Hiệu Điện Não

Xem toàn bộ 130 trang tài liệu này.

Với L

 Z , có thể coi

x n  L 

là tín hiệu được làm trễ L lần của

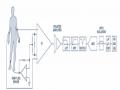
 Các trọng số có thể điều chỉnh được w0, w1, ...wL .

 Bộ lấy tổng số học.

 Một đầu lấy tín hiệu ra với

y(n) 

L

x(n  k)wk. (1.5)

k 0

Các trọng số là các số thực và được điều chỉnh sao cho y(n) giống nhất

với

d(n)

(xem hình 1.4). Việc điều chỉnh các trọng số được coi là thủ tục

thích nghi cho tổ hợp. Theo công thức 1.5, đầu ra là kêt quả tổ hợp tuyến tính từ các thành phần tín hiệu đầu vào.

1.2.2. Bài toán xác định ma trận trọng số tối ưu cho tổ hợp thích nghi

tuyến tính.

Để mô hình hoá thủ tục thích nghi, ta sử dụng các ký hiệu sau:

W là vector trọng số của tổ hợp thích nghi tuyến tính, với

W w0

W là vector có độ dài L  1.

w1 w2 ...

wLT, (1.6)

d n

là tín hiệu huấn luyện mà ta biết trước, trong đó n  Z

là biến

thời gian rời rạc.

X n là vector tín hiệu đầu vào tại thời điểm n , với

X n  x n x n  1x n  2... x n  L T, (1.7)

 

trong đó:

x n : Tín hiệu đầu vào tại thời điểm n ,

xn 1: Tín hiệu được làm trễ 1 lần từ tín hiệu x n,

xn L : Tín hiệu được làm trễ L lần từ tín hiệu x n.

X n 

là vector có độ dài L  1. Bài toán đặt ra là ta muốn nhận được

y(n)

với

y(n)  X T (n)W

sao cho

y(n)

giống nhất với tín hiệu huấn luyện

d n 

theo nghĩa

(n)  d(n)  y( n)

đạt được một cực tiểu. Việc điều chỉnh

các trọng số được coi như là bài toán xác định các phần tử wk

với

k  1,2,..., L , sao cho khi sử dụng công thức (1.5), đầu ra

y(n)

giống nhất

với d(n) .

Lời giải cho bài toán này dựa trên giả thiết rằng tín hiệu X n và d(n)

là tín hiệu dừng theo nghĩa dưới đây.

Định nghĩa 1.1. Dãy dừng là dãy ngẫu nhiên có phân phối xác suất không thay đổi theo thời gian.

Nếu dãy

N (t )

là dừng và có

FN (t0 ), N (t L ) (n(t0 ), n(tL ))

biểu diễn hàm

phân phối của N (t )

tại thời điểm t0 , t1 , …, tL

thì ta có :

FN (t0 ), N (t L ) (n(t0 ), n(tL ))

 FN (t 0 ), N (t L )(n(t0), n( tL)) ,

với

L, 

 Z .

Trong xử lý tín hiệu, tín hiệu dừng được coi như dạng yếu của dãy dừng (xem [1]). Ta có định nghĩa tín hiệu dừng như sau:

Định nghĩa 1.2. Tín hiệu dừng là tín hiệu ngẫu nhiên có moment bậc 1 và 2

không thay đổi theo thời gian.

Nếu tín hiệu S(n) là tín hiệu dừng thì

E[S(n)]  ms(n)

 ms( n  ) , với

  Z .

với

E[S(n1)S(n2)]  Rs( n1, n2)

  Z .

 Rs( n1 , n2 )

 Rs( n1 n2, 0) ,

Bài toán xác định ma trận trọng số tối ưu cho tổ hợp thích nghi tuyến

tính trong [45] yêu cầu

Xn

và d n là tín hiệu dừng theo định nghĩa 1.2

và tìm W * sao cho (n) đạt cực tiểu. Nếu mỗi khi moment bậc 1 và moment

bậc 2 của chúng chuyển thành giá trị cố định khác, ta phải tìm lại ma trận

trọng số tối ưu W *

khác, sao cho tại đó

(n) lại đạt cực tiểu. Sau khi tính

được W * , nếu các thông số của

thay đổi.

X n 

không thay đổi thì W *

cũng không

Các kết quả đạt được trong [45] được trình bày như sau :

Các kết quả ban đầu được N. Wiener đưa ra trong [45]. Tuy chưa giải quyết hoàn toàn được yêu đầu đặt ra nhưng đã là cơ sở quan trọng để những tác giả sau đó phát triển đúng hướng. Lời giải như sau: Nếu hàm để cực tiểu hóa được chọn là   E[2(n)] , thì

  E d 2(n)  W TE X (n)X (n)TW 2E d(n)X(n) TW .

Ma trận trọng số W *

được tính như sau:

W *  R1P , (1.8)

trong đó W *

và

là ma trận trọng số tối ưu, tại đó  đạt giá trị cực tiểu,

R  E[X n X T n ], (1.9)

P  E[d(n)X (n)] . (1.10)

Với giả thiết

Xn

và d n là tín hiệu dừng như trên, các phần tử của R và

P đều là hằng số.

Tuy nhiên, lời giải trên của N. Wiener chưa giải quyết được trường hợp sau: Mỗi khi các thông số thống kê của của tín hiệu X n hoặc tín hiệu huấn

luyện

dn

thay đổi, dẫn đến các phần tử của ma trận R và P thay đổi,

chuyển thành các hằng số khác. Do vậy, một cách tự động W *

phải được tính

lại theo các công thức (1.9), (1.10) và (1.8) (xem [32], [35], [36], [44]).

Nhưng trong thực tế, ta chỉ có được

Xn

bằng cách đo tín hiệu đầu vào

dưới dạng số thực tại những thời điểm n chứ không xác định được tín hiệu

Xn

dưới dạng hàm số nào đó. Do vậy không thể biết được khi nào R thay

đổi để tính lại W * . Vậy lời giải Wiener trong công thức (1.8) chưa đủ để thực

hiện bộ lọc thích nghi.

1.2.3. Thuật toán thích nghi của B. Widrow.

Để giải quyết vấn đề nêu trên, B. Widrow đã đề xuất thay đổi cách tiếp cận, chuyển từ tính trực tiếp W * thành tìm kiếm ngẫu nhiên W * bằng phương pháp lặp [44]. Khi đó bài toán được mô tả tương đương:

Cho công thức lặp tính ma trận trọng số tối ưu như sau :

W n  1W (n ) W (n) ,

trong đó

W n  1 : Ma trận trọng số tại thời điểm n  1.

W (n) : Ma trận trọng số tại thời điểm n ,

W (n) : Tham số hiệu chỉnh tại thời điểm n .

Bài toán đặt ra là :

 Tìm Biểu thức tính

W (n)

sao cho mỗi khi W n  1đạt đến W *,

thì tham sô hiệu chỉnh W (n)  0 và không thay đổi nếu tính chất

dừng của

X n và d(n)

cũng không thay đổi. Nếu tính chất dừng thay

đổi,

W (n)  0

để bắt đầu lại các bước lặp tìm ma trận tối ưu khác.

 Xác định điều kiện để W n  1 có khả năng hội tụ đến W *. Các kết quả đạt được trong [44] được trình bày như sau:

Tham số hiệu chỉnh

W (n)

được B. Widrow và học trò của ông là T.

Hoff đề xuất cho thuật toán LMS :

W (n) 2(n) X(n) ,

trong đó

 : Kích thước bước, quyết định tốc độ hội tụ và độ ổn định của thuật

toán. Dải ổn định của thuật toán được xác định trong công thức sau

1

0    L

. (1.11)

x 2(n  i )

i 0

Thuật toán LMS có ưu điểm nổi bật về tính đơn giản trong tính toán vì

W (n)

được tính chỉ từ đầu vào

Xn

và đầu ra

n

của tổ hợp tuyến

tính (Hình 1.4).

Từ các kết quả trên, thuật toán LMS được tóm tắt như sau :

 Nạp tín hiệu huấn luyện d .

 Gán n  L  1.

 Gán giá trị khởi tạo cho các phần tử của W (n) .

 Chọn  để thuật toán ổn định.

 Lặp

o Gán X (n) : x(n)

x n 1 

x n 2 

...

x n  L T.

o Tính (n) :  d(n) X(n)TW( n) .

o Tính W (n  1) W (n) 2 (n) X(n) .

o n : n  1

o Cho đến khi hết dãy tín hiệu thì dừng lại.

Với việc chuyển thành bài toán tìm kiếm ngẫu nhiên như trên, thuật

toán LMS có khả năng tìm được W *

đối với lớp bài toán

Xn

không phải

là tín hiệu dừng, khi đó  không còn dạng bậc 2, là trường hợp không áp dụng được lời giải Wiener. Tuy nhiên điều kiện ổn định trong công thức (1.11) chưa chính xác khi sử dụng thuật toán LMS trong các mô hình được phát triển từ tổ hợp thích nghi tuyến tính như bộ lọc nhiễu Adaptive FIR, đặc biệt là Adaptive IIR. Cần phải xác định thêm điều kiện cần và đủ cho sự hội tụ của thuật toán LMS. Đây cũng là vấn đề được giải quyết trong chương II.

1.3. Biến đổi sóng nhỏ với bài toán xác định điểm đột biến.

1.3.1. Tính đạo hàm bậc 1 và 2 thông qua biến đổi sóng nhỏ đa thang.

Hàm  x được gọi là sóng nhỏ nếu thoả mãn 2 điều kiện sau:



  x dx



và

 0 , (1.12)



 ((x))2dx



 1 .

sau :

Ta có định nghĩa phép biến đổi sóng nhỏ đối với

f (x)  L2(R)

như

F  ,s   1 f (x ) x dx , (1.13)

s  s

trong đó:

F  ,s : Ký hiệu phép biến đổi sóng nhỏ đối với

tham số trượt  và tham số thang s .

f (x)  L2(R)

tại

Sóng nhỏ

 x , nghĩa là :

s (x)

là kết quả của phép dãn tại thang s đối với sóng nhỏ

 x 1x. (1.14)

 

s

   

s  s 

Sóng nhỏ

 x được gọi là có n moment triệt tiêu nếu và chỉ nếu với

mọi số nguyên dương k  n

thoả mãn



 xk (x)dx



 0 . (1.15)

Theo [4], [6], [11], [23], [24], [25] biến đổi sóng nhỏ tại thang s đối

với hàm

f (x)  L2(R)

bằng s (x) có thể được thực hiện qua phép tích chập:

trong đó

Wf (s,x )  f

* s(x) , (1.16)

Wf (s,x ) : Ký hiệu phép biến đổi sóng nhỏ thông qua phép tích chập đối

với hàm

fx

tại thangs . Qua công thức 1.16, ta thấy rằng Wf (s,x )

là hàm

của thang s và vị trí không gian x .

s(x) : Sóng nhỏ  x được dãn tại thang s (công thức 1.14).

Dấu * là ký hiệu của phép tích chập, được định nghĩa trong công thức

sau:

f * s(x)



 f( )s( x  ) d  . (1.17)



S. Mallat đã đề cập đến trong [14], tại một số trường hợp, có thể hoán vị giữa toán tử tính đạo hàm và toán tử tính tích chập. Tính chất này cho phép

tính trực tiếp đạo hàm bậc n bất kỳ chỉ qua một phép biến đổi sóng nhỏ và có thể sử dụng các thang s khác nhau. Do vậy, cho phép chọn được thang s sao cho phù hợp nhất với từng bài toán có yêu cầu riêng về tính đạo hàm.

Tính chất giao hoán giữa toán tử tính đạo hàm với toán tử tính tích chập

được mô tả như sau: Nếu hàm

f (x ) và (x)

khả vi thì

f * d (x)  d f * ( x) .

dx dx

Để tính đạo hàm bậc 1 và 2, ta đưa vào hai hàm số được định nghĩa như sau:

1(x)

và 2(x)

1(x)  d(x) , (1.18)

dx

và 2(x)  d 2(x) , (1.19)

dx 2

trong đó  x là hàm khả vi và suy giảm nhanh. S.Mallat và W. L. Hwang đề

nghị chọn (x) 

x 2

1 

2 e2, hàm  x được gọi là sóng nhỏ cơ sở Gaussian

s

[43], và được chúng tôi sử dụng để giải quyết bài toán xác định toạ độ điểm đột biến trong chương 3 của luận án.

s

1(x)

và 2(x)

tương ứng

1(x)

và 2(x)

được dãn tại thang s theo

công thức sau :

s

1x

 1

s

1 x,

 

 s 

2(s)  12 x,

s s s

s

1(x)

và 2(x)

được gọi là sóng nhỏ Gauss1 và Gauss2, là 2 sóng nhỏ

s

đã được sử dụng nhiều trong các ứng dụng dò biên của xử lý ảnh. Qua công