CHƯƠNG III LỌC SỐ NHIỀU NHỊP
3.1. MỞ ĐẦU:
Kỹ thuật lọc số nhiều nhịp ngày càng được ứng dụng nhiều trong lĩnh vực xử lý số tín hiệu, như là nó có thể dùng để tăng tốc độ tính toán trong các bộ lọc số bằng cách giảm số lượng các phép nhân phải thực hiện trong 1 giây.
Chúng ta biết rằng trong quá trình xử lý số tín hiệu, bề rộng của dải tần số có thể thay đổi, như là các phép lọc sẽ triệt tiêu các thành phần tần số không mong muốn, thì bề rộng của dải tần của tín hiệu xử lý sẽ được giảm đi và chúng ta giảm tần sộ lấy mẫu cho phù hợp với bề rộng phổ của tín hiệu và như vậy sẽ giảm được số lượng các phép tính trong bộ lọc số.
Do những tính chất ưu việt của nó, kỹ thuật lọc số nhiều nhịp được nghiên cứu trong những năm gần đây và thu được những kết quả khả quan về lý thuyết cũng như ứng dụng kỹ thuật như trong viễn thông, xử lý tiếng nói, xử lý hình ảnh, hệ thống antenna, kỹ thuật audio số, đặc biệt là hai ứng dụng chính vẫn là mã hóa bằng con(subband coding) dùng trong xử lý tiếng nói và phân đường dùng trong viễn thông.
Thành tựu của kỹ thuật lọc số nhiều nhịp trong những năm vừa qua thể hiện ở việc nghiên cứu các hệ thống số nhiều nhịp, như là tổng hợp các bộ lọc phân chia và các bộ lọc nội suy, các bank lọc phân tích và tổng hợp, biểu diễn nhiều pha và cấu trúc nhiều pha.
3.2. THAY ĐỔI NHỊP LẤY MẪU
3.2.1. CÁC ĐỊNH NGHĨA
Để làm quen với khái niệm nhiều nhịp và để theo dõi các quá trình tiếp theo chúng ta cần phải định nghĩa một số khái niệm mới.
Có thể bạn quan tâm!
Xem toàn bộ 140 trang tài liệu này.
a) Định nghĩa hệ thống nhiều nhịp
Nếu trong một hệ thống xử lý số tín hiệu, tần số (hoặc nhịp) lấy mẫu được thay đổi trong quá trình xử lý, thì hệ thống số này được gọi là hệ thống xử lý nhiều nhịp
b) Định nghĩa phép phân chia
Việc giảm tần số lấy mẫu từ giá trị Fs về một giá trị F's (F's < Fs) được định nghĩa là phân chia.
Nếu F's = Fs/M (M >l và nguyên dương) thì ta gọi là phép phân chia theo hệ số M và M gọi là hệ số phân chia.
c) Định nghĩa bộ phân chia
Hệ thống chỉ làm nhiệm vụ giảm tần số lấy mẫu được gọi là bộ phân chia Bộ phân chia được ký hiệu như hình 3.2.1.1
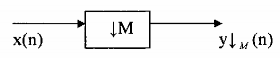
sau:
M: là hệ số phân chia
Hình 3.2.1.1
Để thuận tiện chúng ta có thể dùng ký hiệu toán tử để biểu diễn phép phân chia như
M[x(n)] = y (n) yM (n) (3.2.1.1)
Hay:
M
X(n) y(n) yM (n)
(3.2.1.2)
d) Định nghĩa phép nội suy
Việc tăng tần số lấy mẫu từ giá trị Fs đến một giá trị F’s (Fs < F’s ) được định nghĩa là phép nội suy.
Nếu F’s = LFs (L> 1 và nguyên dương) thì ta gọi là phép nội suy cho hệ số L. và L là phép nội suy.
e) Định nghĩa bộ nội suy
Hệ thống chỉ làm nhiệm vụ tăng tần số lấy mẫu ta gọi là bộ nội suy Bộ nội suy được ký hiệu như trên hình 3.2.1.2
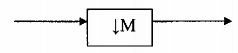
Y L(n)
X(n)
L: hệ số nội suy
Hình 3.2.1.2
Để thuận tiện ta có thể dùng ký hiệu toán tử để biểu diễn phép nội suy như sau:
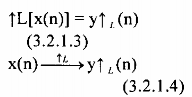
3.2.2. PHÉP PHÂN CHIA THEO HỆ SỐ M
a) Biểu diễn phép phân chia trong miền biến số n
giả sử ta có bộ phân chia theo
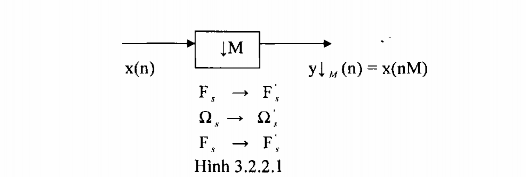
Ta thấy rằng tần số lấy mẫu Fs Của tín hiệu rời rạc xâu sau khi đi qua bộ phân chia này sẽ bị giảm đi M lần, tức là:
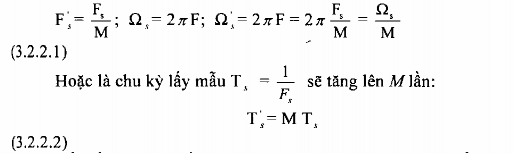
Để hiểu rõ bản chất của quá trình phân chia này ta sẽ biểu diễn dãy vào và dãy ra của bộ phân chia này ở dạng không chuẩn hóa như trên hình 9.2.2.2 (chuẩn hóa ở đây được hiểu là chuẩn hóa bởi chu kỳ lấy mẫu).
![]()
![]()
nM: số nguyên
Hình 3.2.2.2
Như vậy tín hiệu rời rạc trước khi vào bộ phân chia là x (n Ts ) và Sau khi ra khỏi bộ phân chia là x(n Ts).
Ví dụ 3.2.2.1: Cho tín hiệu rời rạc sau đây
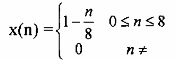
Hãy vẽ xâu bằng đồ thị dưới dạng không chuẩn hoá (theo chu kỳ lấy mẫu ) và chuẩn hoá trước khi vào và sau khi ra khỏi bộ phận chia theo hệ số M = 2.
Giải
Lời giải được cho trên hình 3.2.2.3
chưa chuẩn hóa chuẩn hóa
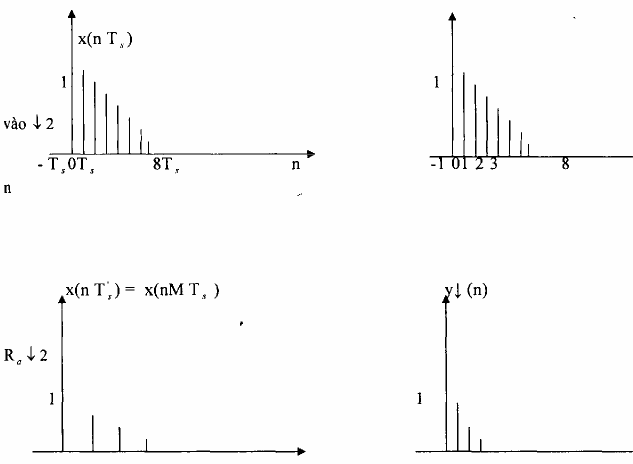
- T’s 0 T’s 4T’s nT’s -1 0 12 3 4 5
(a) ra không chuẩn hoá
(b) tín hiệu vào không chuẩn
(c) tín hiệu vào chuẩn hoá theo chu kỳ lấy mẫu Ts
(d) tín hiệu tín hiệu ra chuẩn hoá theo chu kỳ lấy mẫu T’s = M Ts
Hình 3.2.2.3
Chú ý:
- Ta thấy rằng tín hiệu ra yM(n) chỉ lấy các giá trị của tín hiệu vào x(n) ở các mẫu nM, bởi vì tần số lấy mẫu bị giảm đi M lần sau khi tín hiệu đi qua bộ phân chia theo hệ số M.
- Chiều dài của x(n) bị co lại M lần, tức là L[x(n)]/L[yM (n)] =M
b) Biểu diễn phép phân chia trong miền z.
Chúng ta có thể biểu diễn quá trình phân chia bằng bộ phân chia trong miền z như sơ đồ trên hình 3.2.2.4
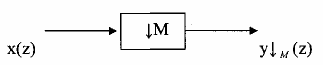
Hình 3.2.2.4
Ta biết rằng trong miền biến số độc lập ta có:
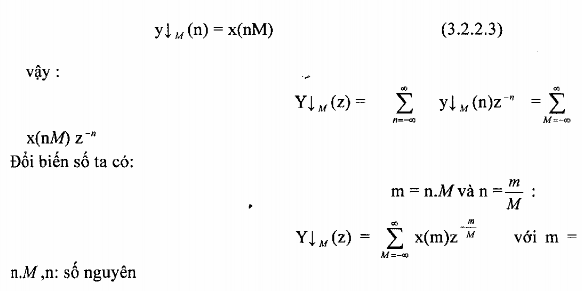
Ta đã biết rằng dãy p(m) được định nghĩa như sau:
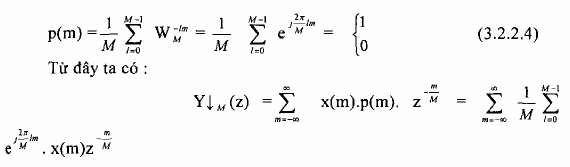
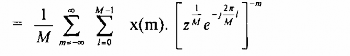
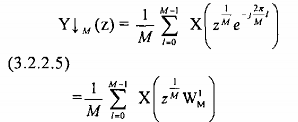
hoặc có thể viết dưới dạng sau đây:
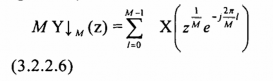
Ví dụ 3.2.2.2
Một tín hiệu x(n) có biến đổi z là X(z) đi qua bộ phân chia với hệ số M = 2, ở đầu ra của bộ phân chia này ta thu được Y2(z). Hãy tìm quan hệ giữa X(z) và Y2(z) nếu xâu có dạng sau đây:
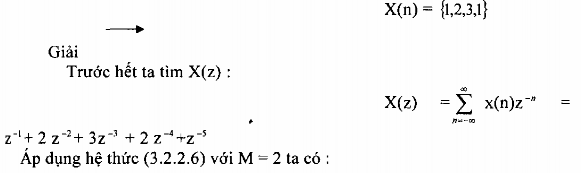
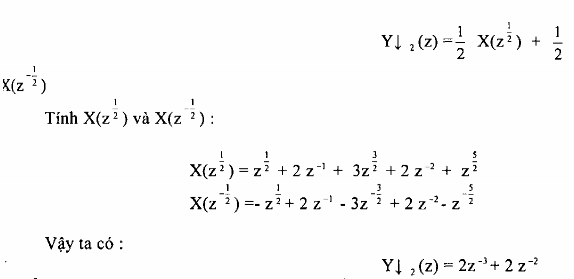
c. Biểu diễn phép phân chia trong miền tần số.
Biểu diễn phép phân chia trong miền tần số chính la việc tìm quan hệ giữa:
Y (ej) = FT[yM(n)]
Và:
X(ej) = FT[x(n)] ( )
Nếu ta đánh giá trị YM(z) là X(z) trên vòng tròn đơn vị của mặt phẳng z thì ta sẽ tìm được quan hệ giữa YM(ej) và X(ej), tức là:
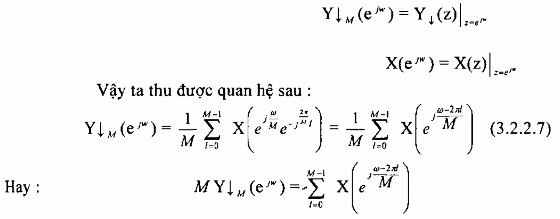
Ví dụ 3.2.2.3
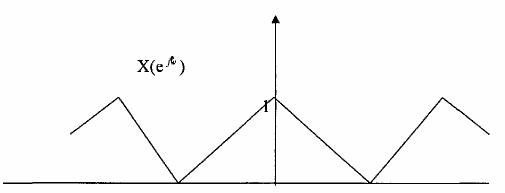
Cho tín hiệu rời rạc x(n) được lấy mẫu từ một tín hiệu tương tự xa(t) tần số lấy mẫu băng tần số Nyquist FNy, x(n) có phổ là X(ej) cho trên hình (3.2.2.5)
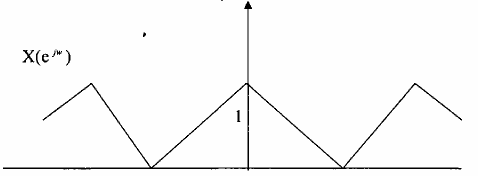

Hình 3.2.2.5
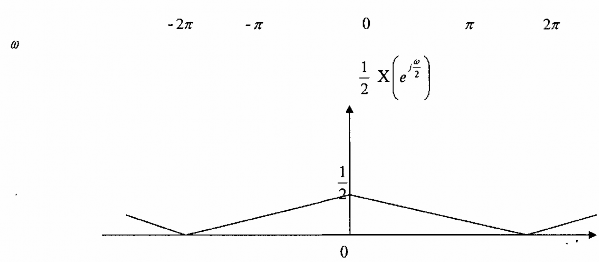
Tín hiệu này dược truyền qua một bộ phân chia có hệ số M = 2 và ở đầu ra ta thu
được Y (n). Hãy vẽ phổ của Y2(n), tức là vẽ Y 2 (ej) theo phổ của X(ej)
Giải
Thay M= 2 vào biểu thức (3.2.2.7) ta có:
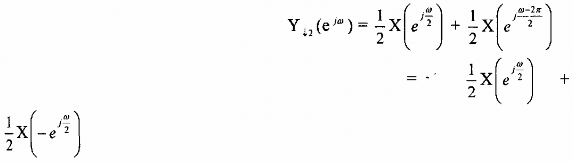
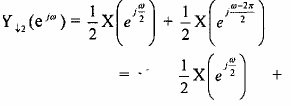
Như vậy phổ Y 2(ej) sẽ là sự xếp chồng phổ của hai thành phần trên kết quả được minh họa như trên hình 3.2.2.6