Thiết Kế Bộ Lọc Fir Pha Tuyến Tính Dùng Cửa Sổ

giống một cách chính xác như là đáp ứng của hệ thống được mô tả bởi pt(1.28) với kích thích là tín hiệu xung đơn vị.

1.2. Thiết kế bộ lọc FIR

1.2.1. THIẾT KẾ BỘ LỌC FIR PHA TUYẾN TÍNH DÙNG CỬA SỔ

1.2.1.1. Nguyên tắc:

Từ đáp ứng tần số mong muốn Hd() với các chỉ tiêu tương ứng, ta lấy biến đổi Fourier ngược để có đáp ứng xung hd():

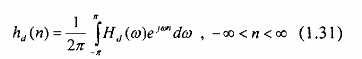
Nói chung, hd(n) thu được sẽ có chiều dài vô h(n) và không nhân quả, ta không thể thực hiện được trong thực tế. Vì vậy, hệ thống phải được sửa lại thành nhân quả và buộc h(n) phải h(n) chế chiều dài của hd(n). Phương pháp đơn giản là cắt bỏ hd(n) từ giá trị n = M-1 và thu được bộ lọc FIR có chiều dài M. Sự "cắt ngọn" này tương đương với phép nhân h(n)g với một hàm cửa sổ (window). Hàm cửa sổ này được định nghĩa như sau:

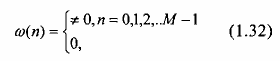
Như vậy, đáp ứng xung của bộ lọc FIR trở thành:

h(n) = hd(n).w(n) (1.33)

Gọi W() là biến đổi Fourier của cửa sổ w(n), từ tính chất nhân của biến đổi Fourier, ta thu được đáp ứng tần số của bộ lọc như sau:

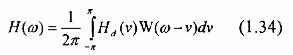
1.2.1.2. Các bước chính của phương pháp cửa sổ: Chọn 4 chỉ tiêu kỹ thuật của bộ lọc số: δ1, δ2, p, s. Xác định đáp ứng xung của mạch lọc lý tưởng. Chọn loại cửa sổ.

Nhân với cửa sổ để có đáp ứng xung của mạch lọc: hd(n) = h(n).w(n). Thử lại trong miền tần số: Hd() = H()*W().

Nếu không thỏa mãn các chỉ tiêu kỹ thuật, ta tăng M và trở lại bước 2.

1.2.1.3. Cửa sổ chữ nhật

Định nghĩa: Cửa sổ chữ nhật có chiều dài M được định nghĩa trong miền thời gian

như sau:

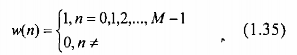
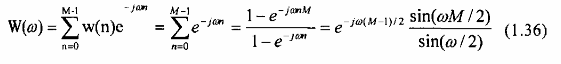
Trường hợp M lẻ, w(n) có dạng đối xứng với tâm đối xứng là n: Biến đổi Fourier của cửa sổ chữ nhật là:

M -1 .

2

Cửa sổ này có đáp ứng biên độ là:

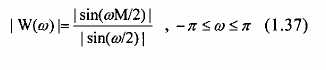
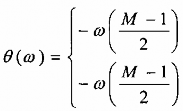
và có đáp ứng pha tuyến tính từng đoạn:

, khi sin (M)/2  0

, khi sin (M)/2 < 0

1.38

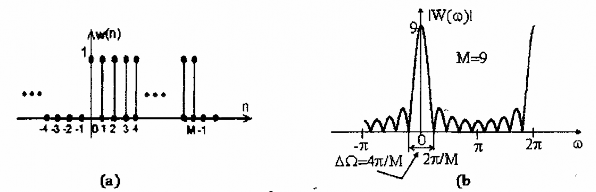
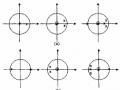
Hình 1.14: (a) Cửa sổ chữ nhật có chiều dài M = 9

(b) Đáp ứng biên độ cửa sổ chữ nhật

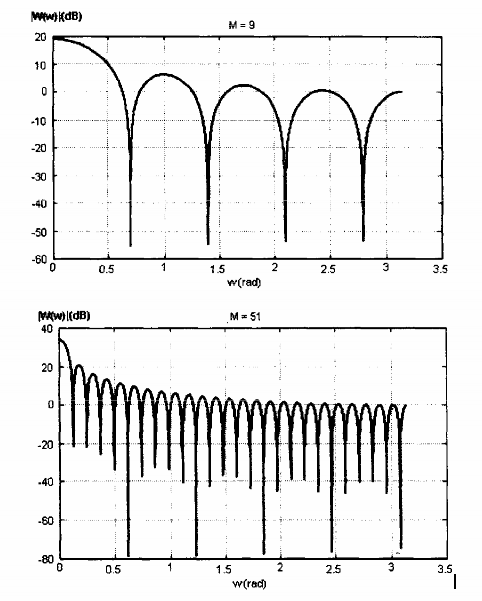
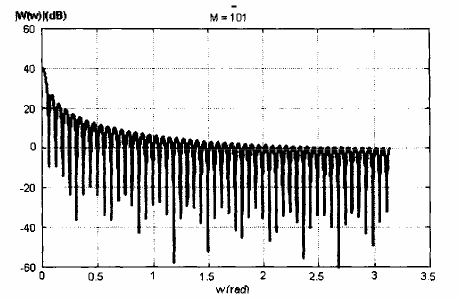
Hình 1.15: Các đáp ứng biên độ (db) của cửa sổ chữ nhật với M = 9. M = 51 và M-101

Các tham số (các tham số này cũng được định nghĩa chung cho các loại cửa sổ khác):

- Độ rộng của múi chính DW (được tính bằng 2 lần dải tần số từ  = 0 đến p, tần số p tương ứng với giá trị zero của múi chính), đối với cửa sỗ chữ nhật:

DW = 4p/M. (1.39)

- Tỉ số giữa đỉnh của múi bên đầu tiên và đỉnh của múi chính, ký hiệu ta có:

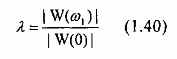
với 1 là tần số tương ứng với đỉnh của múi bên đầu tiên, với cửa sổ chữ nhật w1 = 3p/M. Tham số này thường được tính theo dự như sau:

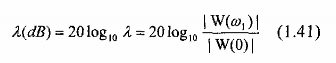
Người ta cũng thường xét đến một đại lượng ngược lại, đó là tỉ số của đỉnh múi chính và đỉnh múi bên đầu tiên, ký hiệu h, ta có:

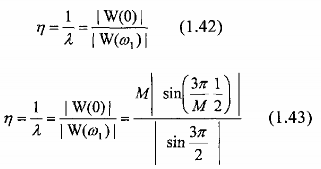
đối với cửa sổ chữ nhật:

Sau đây là giá trị của h tương ứng với các độ dài M khác nhau:

M = 6 ® h = 4,2426; M = 9 ® h = 4,1000; M = 10 ® h = 4,7014; M = 100 ® h = 4,7106;...

và M ® ¥ ~ thì h » 4,712. Ta thấy, khi M > 10 tham số gần như không đổi.

Hình 1.14.a trình bày cửa sổ chữ nhật trong miền thời gian, hình 1.14.b là đáp ứng biên độ của cửa sổ chữ nhật với M = 9. Các tham số tương ứng như sau:

DW = 4p/M = 1,3963 rad; 1 = -13,0643dB; h = 4,1000

Hình 1.11 trình bày đáp ứng biên độ của cửa số chữ nhật với M lần lượt là: 9,11 và

101.

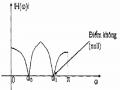
Hiện tượng Gibbs 1

Để giới hạn chiều dài đáp ứng xung h(n) của bộ lọc lý tưởng, ta đã nhân với hàm cửa sổ w(n). Đáp ứng tần số của bộ lọc thực tế có được từ tích chập (131). Đối với bộ lọc

lý tưởng, đáp ứng biên độ chuyển đột ngột từ 1 xuống 0 (hoặc ngược lại) ở tần số cắt. Nhưng đối với bộ lọc thực tế, do tích chập trong miền tần số sẽ gây dao động ở dải thông và dải chặn xung qu../ Anh tần số cắt c. Sự phát sinh các dao động này được gọi là hiện tượng Gibbs.

Ví dụ 1.4:

Hãy thiết kế bộ lọc FIR pha tuyến tính với các chỉ tiêu kỹ thuật sau đây:

δ1 = 0.01, δ2 = 0.01, p = /4 - /10 = 0,7226,  = /4 + /10 = 0,8482 và  = (p + s/2

= /4.

Giải:

- Chọn cửa sổ chữ nhật W(n) nhân quả và có tâm đối xứng tại (M- 1)/2.

- Để minh họa hiện tượng Gibbs, ta chọn đáp ứng tần số của bộ lọc thông thấp lý tưởng, ta có:

Lấy biến đổi Fourier ngược, theo pt(1.28), ta được đáp ứng xung h(n):

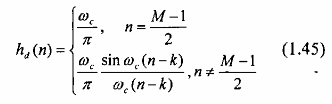
Ta thấy hd(n) có chiều dài vô h(n), không nhân quả và có tâm đối xứng là k trong miền thời gian. Nếu ta chọn k = (M- 1)/2 thì hơn có tâm đối xứng tại (M- 1)/2.

Nhân h(n) với cửa sổ chữ nhật w(n), đáp ứng xung của bộ lọc trở nên nhân quả và có chiều dài hữu h(n):

h(n) = hd(n) .w(n)

Hình 1.16. Minh họa đáp ứng xung h(n) với M = 61.

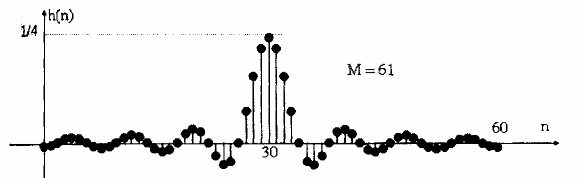
Hình 1.16: Đáp ứng xung h(n) được cắt từ hd(n) và cửa sổ chữ nhật M = 61

Đáp ứng tần số của hệ thống được thiết kế là:

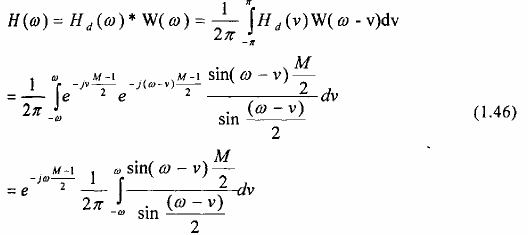
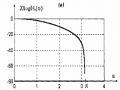
Hình 1.18 vẽ đặc tuyến đáp ứng biên độ của bộ lọc với M = 9, M = 61 và M = 101.

Ta thấy, khi tăng M, độ gợn sóng dải thông và dải chặn có biên độ không giảm và trong cả ba trường hợp, chỉ tiêu về độ gợn đã đề ra chưa được thỏa mãn. Tuy nhiên, độ rộng dải quá độ được cải thiện (thu hẹp lại) khi M tăng.

Để làm giảm những gợn sóng lớn trong cả dải thông và dải chặn, chúng ta có thể sử dụng các hàm cửa sổ mà nó chứa đựng một đỉnh nhọn và suy giảm dần về zero thay vì đột ngột như hàm cửa sổ hình chữ nhật.

Một số hàm cửa sổ tiêu biểu thường được dùng trong thiết kế mạch lọc FIR được trình bày trong bảng 1.1 và dạng của một số cửa sổ được trình bày trong hình 1.17. Những hàm cửa sổ này có các múi bên (sidelode) thấp hơn so với cửa sổ hình chữ nhật. Tuy nhiên, với cùng giá trị M chiều rộng của múi chính của các hàm cửa sổ này cũng rộng hơn so với cửa sổ hình chữ nhật. Do đó, các hàm cửa sổ này có tác dụng làm trơn (smoothing) đáp ứng tần số thông qua tích chập trong miền tần số, và kết quả là dải quá độ của lọc FIR rộng hơn. Để giảm độ rộng của dải quá độ, chúng ta tăng chiều dài cửa sổ, kết quả là mạch lọc lớn hơn.

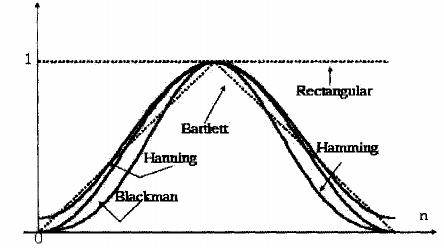
Hình 1.17. Dạng (bao hình) của một số hàm cửa sổ trong miền thời gian

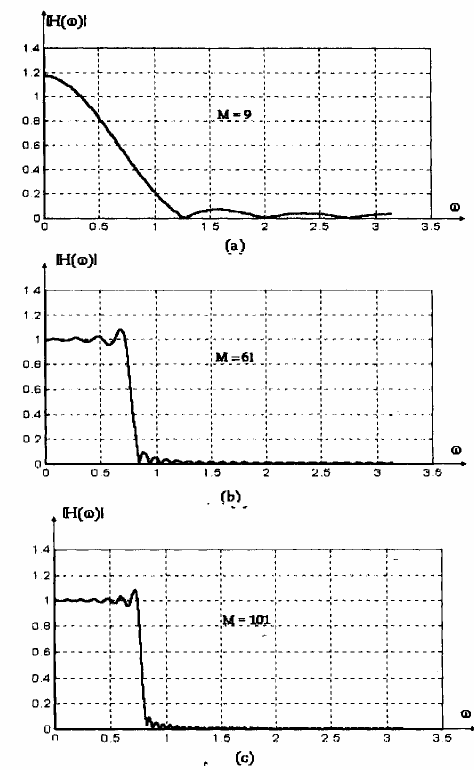
Hình 1.18: Đáp ứng biên độ của bộ lọc thông thấp được thiết kế với cửa sổ chữ nhật. (a) M = 9, (b) M = 61, (c) M = 101

Bảng 1.1. Các hàm cửa sổ

Bartlett (triangular)

2n , Với 0  n M 1 M 1 2n 2 - 2n , Với 2n < n  M - 1 M 1 M 1
Blackman	w(n) = 0.42 - 0.5cos 2π n -+ 0.08 scos 4π n M 1 M 1
Hamming	w(n) = 0.54 - 0.46 cos 2π n M 1
H(n)ning	w(n) = 1 (1 - cos 2π n ) 2 M 1
Kaiser	I⎡M 11 ⎛ 2n1⎞⎤ ⎢⎢β 2 ⎜ M 1 ⎟⎥⎥ ⎣⎝⎠⎦ I⎡⎛M 1⎞⎤ ⎢β⎜2 ⎟⎥ ⎣⎝⎠⎦
Lanczos	⎧⎡2π⎛n M 1⎞⎤⎫ ⎪⎢⎜2 ⎟⎥⎪ ⎪sin⎢⎝⎠⎥⎪ ⎪⎢ M 1 ⎥⎪ ⎪⎢⎥⎪ w(n) = ⎨⎣⎦⎛M 1 ⎞⎬ ⎪⎜ n ⎟⎪ ⎪2π⎜ 2⎟⎪ ⎪⎜⎜M 1⎟⎟⎪ ⎪⎪⎝ 2 ⎠⎪⎪ ⎩⎭
Tukey	1, với n M 1 M 1 , 0 <  < 1 2 2 ⎡⎛ n  (1 α)⎛M 1⎞⎞⎤ 1 ⎢⎜⎜2 ⎟⎟⎥ ⎢1  cos⎜⎝⎠⎟⎥, 2 ⎢⎜ (1 α)⎛M 1⎞⎟⎥ ⎢⎜⎜2 ⎟⎟⎥ ⎣⎝⎝⎠⎠⎦ Với M 1 n  M 1 M 1 2 2 2

Có thể bạn quan tâm!

• Xử lý tín hiệu số 2 Phần 1 - 1
• Xử lý tín hiệu số 2 Phần 1 - 2
• Đáp Ứng Biên Độ (Db) Của Bộ Lọc Thông Thấp Có Tần Số Cắt Là
• Đặc Tuyến Ứng Biên Độ Của Bộ Lọc Fir Pha Tuyến Tính Trong Ví Dụ 5.7
• Các Bước Thiết Kế Bộ Lọc Fir Bằng Phương Pháp Lấy Mẫu Tần Số

Xem toàn bộ 112 trang tài liệu này.

Ghi chú: Cửa sổ Kaiser là một cửa sổ gần tối ưu, nó được thành lập từ hàm Bessel biến dạng loại một bậc không I0(x). Trong công thức định nghĩa cửa sổ Kaiser (Bảng