KHOA CÔNG NGHỆ THÔNG TIN
BỘ MÔN ĐIỆN TỬ VIỄN THÔNG
PHÙNG TRUNG NGHĨA, ĐỖ HUY KHÔI
GIÁO TRÌNH
XỬ LÝ TÍN HIỆU SỐ 2
NĂM 2008
CHƯƠNG I THIẾT KẾ BỘ LỌC SỐ
Có thể bạn quan tâm!
-
Xử lý tín hiệu số 2 Phần 1 - 2 -
Thiết Kế Bộ Lọc Fir Pha Tuyến Tính Dùng Cửa Sổ -
Đáp Ứng Biên Độ (Db) Của Bộ Lọc Thông Thấp Có Tần Số Cắt Là
Xem toàn bộ 112 trang tài liệu này.
Như chúng ta đã phân tích trong các chương của Xử lý tín hiệu I, hầu hết các hệ thống LTI đều có chức năng của bộ lọc. Vì vậy, vấn đề thiết kế bộ lọc số đóng vai trò quan trọng trong xử lý tín hiệu số. Có nhiều phương pháp thiết kế các bộ lọc số đã được đề xuất và ứng dụng trong thực tế. Chương này sẽ trình bày các phương pháp thiết kế cơ bản và ứng dụng của nó để thiết kế các bộ lọc khác nhau.
1.1. Thiết kế bộ lọc bằng cách đặt các cực và zeros trên mặt
Đây là phương pháp thiết kế lọc số đơn giản và có thể áp dụng cho nhiều loại bộ lọc FIR cũng như IIR. Tuy nhiên, để có một đáp ứng tần số theo ý muốn, trong một số trường hợp, ta cần phải thêm vào các cực hoặc zero theo thủ tục thử và sai.
Như chúng ta biết, vị trí của các cực và zeros trên mặt phẳng phức mô tả duy nhất hàm truyền đạt H(z), khi hệ thống có tính ổn định và nhân quả. Vì vậy nó cũng qui định đặc tính số của hệ thống.
Phương pháp thiết kế mạch lọc số bằng cách đặt các cực và zeros trên mặt phẳng phức dựa trên nguyên lý cơ bản là: đặt các cực tại các điểm gần vòng tròn đơn vị và ở các vị trí tương ứng với các tần số trong dải thông, đặt các zeros ở các điểm tương ứng với các tần số trong dải triệt. Hơn nữa, cần phải tuân theo các ràng buộc như sau:
1. Tất cả các cực phải được đặt trong vòng tròn đơn vị để cho bộ lọc ổn định. Tuy nhiên, các zeros có thể đặt ở vị trí bất kỳ trong mặt phẳng z.
2. Tất cả các cực và các zeros phức phải xuất hiện với các cặp liên hợp phức để các hệ số của bộ lọc có giá trị thực.
Với một tập cực - zeros đã cho, hàm truyền đạt H(z) của lọc có biểu thức:
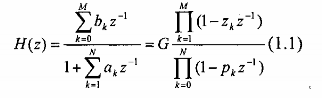
Ở đây G là hằng số độ lợi (gain constant) nó được chọn để chuẩn hóa đáp ứng tần số. Ở một tần số xác định nào đó, ký hiệu là 0, G được chọn sao cho:
|H(0)| = 1
Với 0 là tần số trong dải thông của bộ lọc. Thông thường N (bậc của bộ lọc) được chọn bằng hoặc lớn hơn M để cho bộ lọc có số cực không tầm thường (nontrivial) bằng hoặc nhiều hơn zeros.
Phương pháp này được dùng để thiết kế một số bộ lọc đơn giản nhưng quan trọng như: lọc thông thấp, thông cao, thông dải, dải chặn, lọc răng lược, bộ cộng hưởng số, bộ dao động số,.... Thủ tục thiết kế cũng thuận tiện khi thực hiện trên máy tính.
1.1.1. LỌC THÔNG THẤP, THÔNG CAO VÀ THÔNG DẢI
1.1.1.1. Lọc thông thấp và thông cao:
Với lọc thông thấp, khi thiết kế các cực phải được đặt ở các điểm gần vòng tròn đơn vị trong vùng tần số thấp (gần = 0) và các zeros phải được đặt gần hay trên vòng tròn đơn vị tương ứng với các điểm tần số cao (gần = ), ngược lại cho lọc thông cao. Hình
1.1 Minh họa cho việc đặt các cực và zeros của ba bộ lọc thông thấp và ba bộ lọc thông cao.
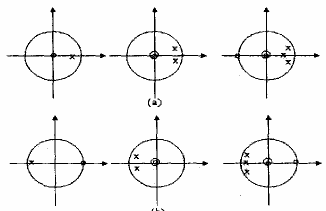
Hình 1.1: Đồ thị cực zeros cho các bộ lọc
(a) Lọc thông thấp; (b) Lọc thông cao
Đáp ứng biên độ và pha cho bộ lọc đơn cực có hàm truyền đạt là:
Được vẽ trong hình 1.1 với a = 0,9. Độ lợi G được chọn là 1- a, để cho lọc có độ lợi bằng 1 ở tần số = 0 và độ lợi ở tần số cao tương đối nhỏ.
Thêm vào một zeros ở z = - 1 sẽ làm đáp ứng suy giảm nhiều hơn ở tần số cao khi
đó lọc có hàm truyền đạt là:
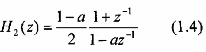
Đặc tuyến của đáp ứng tần số của hai bộ lọc H1(z) và H2(z) cùng được vẽ trên hình
1.2. Ta thấy, biên độ của H2(Z) giảm về 0 khi = n.
Tương tự, ta thu được các bộ lọc thông cao đơn giản bằng cách lấy đối xứng các điểm cực - zero của mạch lọc thông thấp qua trục ảo của mặt phẳng z. Ta thu được hàm truyền đạt:
Đặc tuyến của đáp ứng tần số của mạch lọc thông cao được vẽ trong hình 1.3 với a
= 0,9.
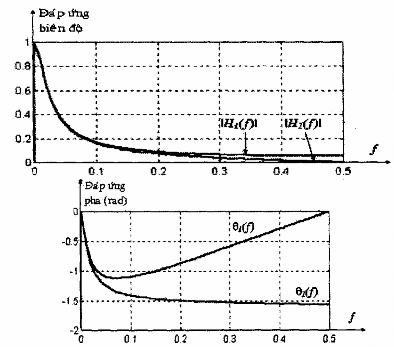
Hình 1.2: Đáp biên độ, đáp ứng pha của bộ lọc 1 cực H1(z) =
1 0.9 1 0.9z 1
của bộ lọc 1 cực -
1 zero H (z) = 1 0.9
1 z 1
2 2 1 0.9z 1
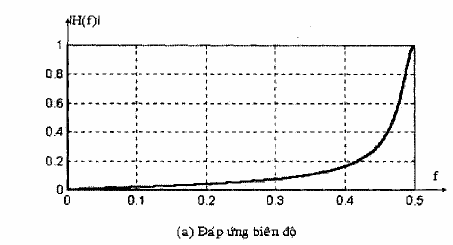
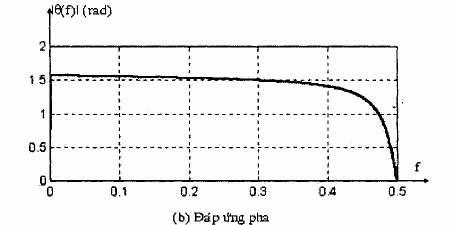
Hình 1.3: Đáp ứng biên độ và đáp ứng pha của bộ lọc thông cao có hàm truyền đạt H =
⎡1 0.9 ⎤⎡1 z 1 ⎤
⎢⎣ 2 ⎥⎦⎢1 0.9z 1 ⎥
⎣⎦
L 2 JLI + o.9z-r -1
Ví dụ 1.1:
Một lọc thông thấp hai cực có hàm truyền đạt là: H(z) =
G
(1 Pz1)2
Hãy xác định giá trị của G và p sao cho đáp ứng tần số H thỏa điều kiện:
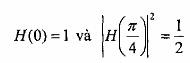
Giải: Tại = 0, ta có:
H(0) =
G
(1 p)2
= 1. Suy ra: G = (1 -p)2.
Tại =
ta có:
4
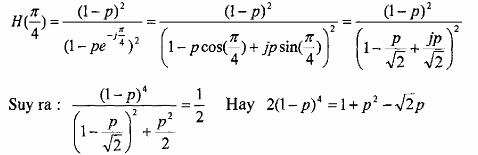
Giải phương trình trên ta được: P = 0,23.
Kết quả: H(0) =
0,458
1 0,23z 1)2
1.1.1.2. Lọc thông dải:
Các nguyên tắc tương tự có thể được áp dụng để thiết kế mạch lọc thông dải. Một cách cơ bản, lọc thông dải chứa một hay nhiều cặp cực phức gần vòng tròn đơn vị, trong lân cận của băng tần mà nó hình thành dải thông của bộ lọc.
Ví dụ 1.2:
Hãy thiết kế mạch lọc thông dải hai cực có tâm của băng tần ở =
đáp ứng tần
2
số H() = 0 khi = 0 và = và đáp ứng biên độ của nó là
j
1 tại =
2
j
4.
9
Giải: Rõ ràng bộ lọc phải có 2 cực tại: p1 =
= - 1. Vậy hàm truyền đạt của nó là:
re 2
và p1 =
re 2 và zero tại z = 1 và z
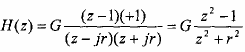
Hệ số khuếch đại G được xác định bằng cách tính H() của bộ lọc ở tần số = .
2
Ta có:
Giá trị của r được xác định bằng cách tính H(w) tại =
4. Ta có:
9
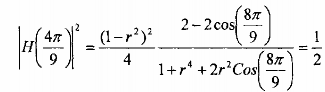
Hay: 1,94(1 -r2)2 = 1 - 1,88r2 +r4.
Giải phương trình ta được r2
= 0,7. vậy: H(z) = 1- z-2
0,15 2
1 0,7z
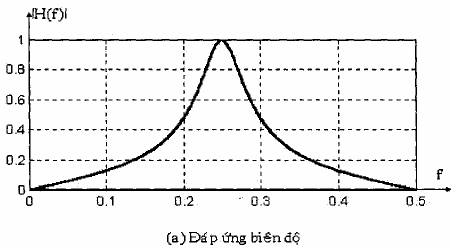
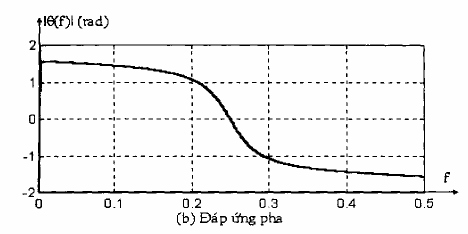
Hình 1.4: Đáp ứng biên độ và đáp ứng pha của bộ lọc thông dải có hàm truyền đạt là:
H(z) =
⎡ 1- z-2 ⎤
0.15⎢1 0,7z ⎥
⎣⎦
zero lên đáp ứng tân sô của hệ thống. Rõ ràng, đây chưa phải là phương pháp tốt cho việc thiết kế mạch lọc số, để có một đặc tuyến của đáp ứng tần số như ý muốn. Các phương pháp thiết kế tốt hơn, được ứng dụng trong thực tế sẽ được trình bài trong phần sau.
1.1.2. BỘ CỘNG HƯỞNG SỐ (DIGITAL RESONATOR)
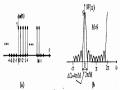
Một bộ cộng hưởng số là một bộ lọc thông dải có hai cực đặc biệt, đó là cặp cực phức được đặt ở gần vòng tròn đơn vị (hình 1.1.a). Biên độ của đáp ứng tần số được vẽ trong hình 1.1.b. Ta thấy, đáp ứng biên độ lớn nhất ở tần số tương ứng của cực và đây là tần số cộng hưởng của mạch lọc.
Để thiết kế một bộ cộng hưởng số với đỉnh cộng hưởng ở tại hay gần tần số = 0
ta chọn cặp cực phức như sau:
P1 = rejvà P2 = re-jvới 0 < r < 1 (1.6)
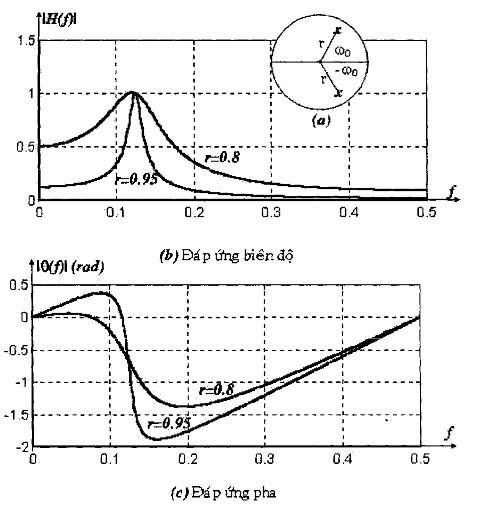
Hình 1.5: (a) Đồ thị cực zeros. (b) Đáp ứng biên độ. (c) Đáp ứng pha của 2 bộ cộng hưởng: một bộ có r = 0.8, bộ còn lại có r = 0.95
Ngoài ra, ta có thể chọn thêm các zero. Mặc dù có nhiều khả năng chọn lựa khác nhau, nhưng có hai trường hợp thường được chọn. Một là thêm vào một zero tại gốc tọa độ. Hai là chọn một zero ở z = 1 và một zero ở z = -1. Sự chọn lựa này có thể khử hoàn toàn đáp ứng của bộ lọc tại = 0 và = .
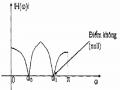
1.1.3. BỘ LỌC DẢI KHẤC (NOTCH FILTER)
Bộ lọc dải khấc là một bộ lọc dải chân có dải tần số chẵn rất hẹp như một vết khấc. Hình 1.6 minh họa đặc tuyến đáp ứng tần số của một bộ lọc dải khấc có độ lợi giảm bằng 0 ở các tần số 0 và 1. Bộ lọc dải khấc được ứng dụng trong những trường hợp mà một vài thành phần tần số cần phải loại bỏ.